Finding the Slopes of Parallel and Perpendicular Lines
How do we know if two distinct lines are parallel, perpendicular, or neither? To make that determination, we need to review some background knowledge about slope.
Concept 1: When two points are given, the slope of a line can be algebraically solved using the following formula:
Slope Formula
The slope,[latex]m[/latex], of a line passing through two arbitrary points [latex]\left( {{x_1},{y_1}} \right)[/latex] and [latex]\left( {{x_2},{y_2}} \right)[/latex] is calculated as follows…
Concept 2: When a linear equation is given, we can find the slope by transforming it into the Slope-Intercept Form. The value of slope will stand out, as it is the coefficient of the linear term ([latex]x[/latex]-term).
Slope-Intercept Form of a Line
The linear equation written in the form [latex]y = mx + b[/latex] is in slope-intercept form where:
Now, suppose we have two distinct and nonvertical lines, [latex]{\ell _1}[/latex] and [latex]{\ell _2}[/latex] in Slope-Intercept Form.
- Line 1:
- Line 2:
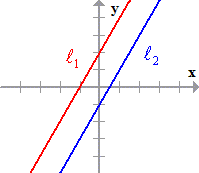
Parallel Lines: The lines are parallel if their slopes are equal or the same. That means
- Equal Slopes:
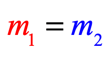
- Graph:
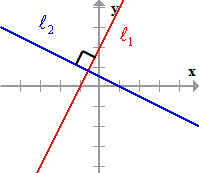
Perpendicular Lines: The lines are perpendicular if their slopes are opposite reciprocals of each other. Or, if we multiply their slopes together, we get a product of [latex] – \,1[/latex]. These lines intersect at a ninety-degree angle, 90°.
- Opposite Reciprocal Slopes:
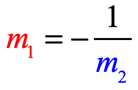
- Product of Slopes:

- Graph:
Examples of How to Find the Slopes of Parallel and Perpendicular Lines
Example 1: Line 1 passes through the points [latex]\left( {1,3} \right)[/latex] and [latex]\left( {4,9} \right)[/latex], while line 2 passes through [latex]\left( {2,5} \right)[/latex] and [latex]\left( { – \,2, – \,3} \right)[/latex]. Tell whether these lines are parallel, perpendicular, or neither.
Begin by finding the slope value of each line using the Slope Formula.
- For the points [latex]\left( {1,3} \right)[/latex] and [latex]\left( {4,9} \right)[/latex]
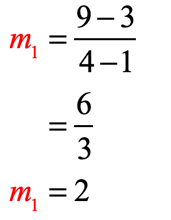
- For the points [latex]\left( {2,5} \right)[/latex] and [latex]\left( { – \,2, – \,3} \right)[/latex]
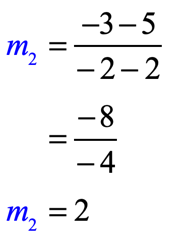
Since their slopes are equal or the same, they are parallel lines. Another way of saying it…
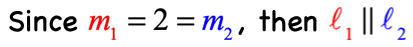
NOTE: The symbol [latex]\parallel [/latex] (two side-by-side vertical lines) means that the lines are parallel to each other.
Example 2: One line is passing through the points [latex]\left( { – \,7,0} \right)[/latex] and [latex]\left( { – \,1, – \,12} \right)[/latex]. Another line is passing through [latex]\left( { – \,1,1} \right)[/latex] and [latex]\left( { – \,15, – \,6} \right)[/latex]. Tell whether these lines are parallel, perpendicular, or neither.
Start finding the slopes of the lines.
- For the points [latex]\left( { – \,7,0} \right)[/latex] and [latex]\left( { – \,1, – \,12} \right)[/latex]:
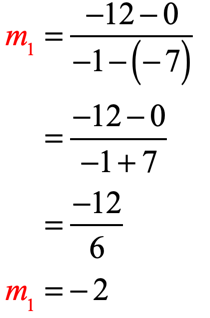
- For the points [latex]\left( { – \,1,1} \right)[/latex] and [latex]\left( { – \,15, – \,6} \right)[/latex]:
![msub2 = /[-15-(-1)] = (-6-1)/(-15+1)=1/2](https://www.chilimath.com/wp-content/uploads/2019/02/ppls-ex2b.png)
If I take the first slope [latex]{m_1} = – \,2[/latex] and get its reciprocal (flip or invert it), I get [latex]{1 \over { – \,2}}[/latex]. Then if I negate or switch the sign, I arrive at [latex]{1 \over 2}[/latex] which is the second slope [latex]{m_2} = {1 \over 2}[/latex]. That makes the slopes to be opposite reciprocals of each other. Therefore, these lines are perpendicular lines.
Another way to verify perpendicularity is to multiply the slopes. If the product is [latex]{ – \,1}[/latex] then we have perpendicular lines, which is the case here!
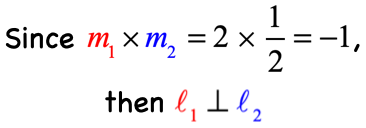
NOTE: The symbol [latex] \bot [/latex] (inverted letter T) means that the lines are perpendicular to each other.
Example 3: A line passes through the points [latex]\left( {4, – \,3} \right)[/latex] and [latex]\left( {0, – \,15} \right)[/latex]. Another line passes through [latex]\left( { – \,2, – \,8} \right)[/latex] and [latex]\left( {4, – \,10} \right)[/latex]. Tell whether these lines are parallel, perpendicular, or neither.
Just like in previous problems, start solving for the slope for each pair of points.
- For the points [latex]\left( {4, – \,3} \right)[/latex] and [latex]\left( {0, – \,15} \right)[/latex]:
![msub1 = [-15-(-3)]/(0-4) = (-15+3)/(0-4) = 3](https://www.chilimath.com/wp-content/uploads/2019/02/ppls-ex3a.png)
- For the points [latex]\left( { – \,2, – \,8} \right)[/latex] and [latex]\left( {4, – \,10} \right)[/latex]:
![msub2 = [-10-(-8)]/ = (-10+8)/(4+2) = (-1)/3](https://www.chilimath.com/wp-content/uploads/2019/02/ppls-ex3b.png)
The product of their slopes is [latex]{ – \,1}[/latex], thus these lines are perpendicular to each other.
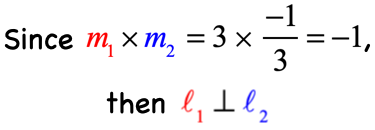
Example 4: The first line passes through points [latex]\left( {0, – \,2} \right)[/latex] and [latex]\left( {1,3} \right)[/latex] while a second line passes through [latex]\left( { – \,9,7} \right)[/latex] and [latex]\left( {1,9} \right)[/latex]. Are they parallel, perpendicular or neither?
- For the points [latex]\left( {0, – \,2} \right)[/latex] and [latex]\left( {1,3} \right)[/latex]:
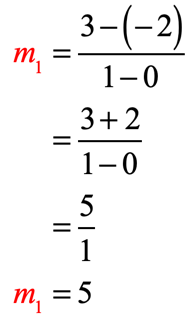
- For the points [latex]\left( { – \,9,7} \right)[/latex] and [latex]\left( {1,9} \right)[/latex]:
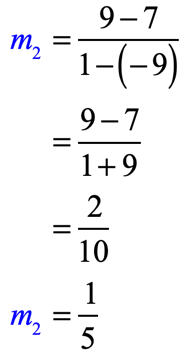
In this case, the slopes are not equal so they are not parallel. The slopes are just the reciprocal of each other. Remember, they must be the opposite reciprocal in order to meet the requirement of perpendicularity. Just like in our previous examples, you can also check by multiplying the slopes. Here you get [latex] + 1[/latex] and not [latex] – 1[/latex], so these lines are not perpendicular either.
Therefore, the final answer is “neither“!
Example 5: Tell whether the line [latex]y = {4 \over 3}x + 2[/latex] is parallel, perpendicular or neither to the line passing through [latex]\left( {1,1} \right)[/latex] and [latex]\left( {10,13} \right)[/latex].
The given equation of the line is in the Slope-Intercept Form [latex]\left( {y = mx + b} \right)[/latex]. We can easily identify the slope, as it is the coefficient of the [latex]x[/latex]-term. Thus, its slope is [latex]{m_1} = {4 \over 3}[/latex]. The next step is to solve for slope between the two points.
For the points [latex]\left( {1,1} \right)[/latex] and [latex]\left( {10,13} \right)[/latex]:
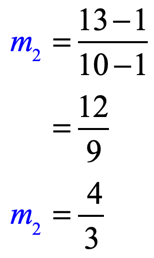
By having the same slopes, they are parallel lines.
Example 6: Tell whether the lines [latex]5x + 11y = – 11[/latex] and [latex] – \,33x + 15y = 5[/latex] are parallel or perpendicular to each other. Otherwise, say neither.
Both linear equations are expressed in the Standard Form [latex]\left( {Ax + By = C} \right)[/latex]. We need to transform each equation of the line from Standard Form to Slope Intercept Form [latex]\left( {y = mx + b} \right)[/latex] because the value of slope is easily identifiable.
- Transform [latex]5x + 11y = – 11[/latex].
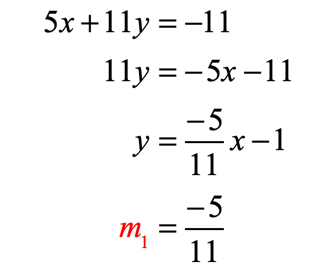
- Transform [latex] – \,33x + 15y = 5[/latex]:
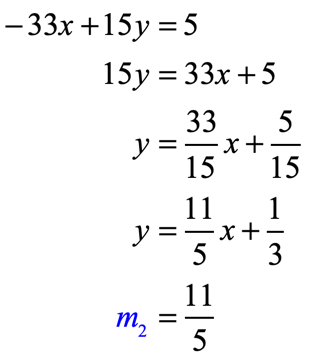
Since the slopes are opposite reciprocals of each other (or their product equals [latex] – 1[/latex] ), they are perpendicular lines.
Example 7: Are the lines parallel, perpendicular or neither that are passing through the pairs of points?
- Line 1:
[latex]\left( {5,7} \right)[/latex] and [latex]\left( {7,5} \right)[/latex]
- Line 2:
[latex]\left( {0,13} \right)[/latex] and [latex]\left( {13,0} \right)[/latex]
Solution:
Calculate the slope of each pair of points where the line passes through.
- For the points [latex]\left( {5,7} \right)[/latex] and [latex]\left( {7,5} \right)[/latex]:
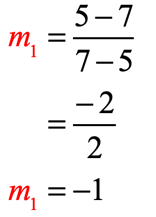
- For the points [latex]\left( {0,13} \right)[/latex] and [latex]\left( {13,0} \right)[/latex]:
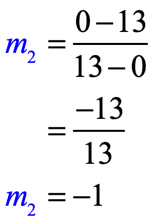
They have equal slopes, therefore the lines are parallel to each other!
Example 8: Are the lines parallel, perpendicular or neither that are passing through the pairs of points?
Line 1:
[latex]\left( {14,1} \right)[/latex] and [latex]\left( {6, – 1} \right)[/latex]
Line 2:
[latex]\left( { – 1,2} \right)[/latex] and [latex]\left( {2,14} \right)[/latex]
Solution:
- For the points [latex]\left( {14,1} \right)[/latex] and [latex]\left( {6, – 1} \right)[/latex]:
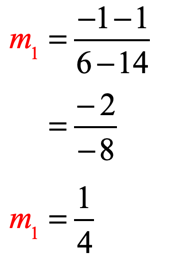
- For the points [latex]\left( { – 1,2} \right)[/latex] and [latex]\left( {2,14} \right)[/latex]:
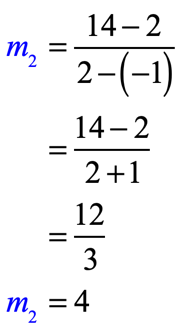
The slopes are neither equal nor opposite reciprocals. The answer is “neither“.
Example 9: Tell whether the lines [latex] – \,49x + 7y = – \,2[/latex] and [latex] – \,28x + 4y = 3[/latex] are parallel or perpendicular to each other. Otherwise, say neither.
Solution:
Transform each equation of the line from Standard Form [latex]\left( {Ax + By = C} \right)[/latex] to
- Transform [latex] – \,49x + 7y = – \,2[/latex]:
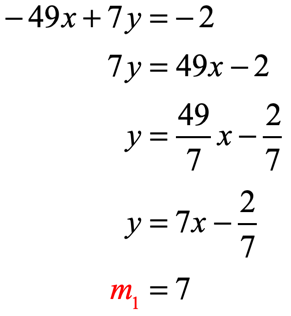
- Transform [latex] – \,28x + 4y = 3[/latex]:
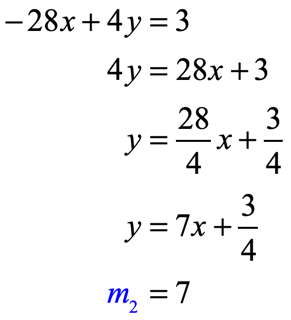
The slopes are the same. They are parallel lines.
You may also be interested in these related math lessons or tutorials:
