The Distance Formula

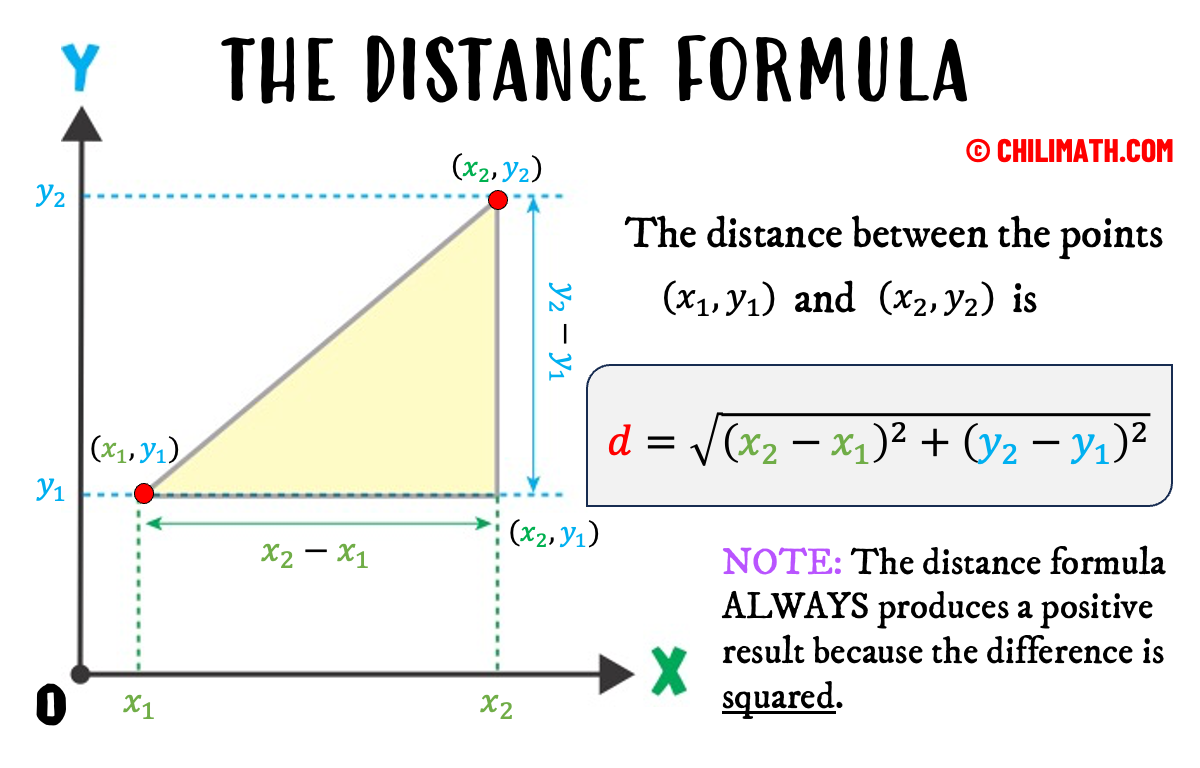
the distance formula visually explained

The Distance Formula is a useful tool for calculating the distance between two points that can be arbitrarily represented as points [latex]A[/latex] [latex]\left( {{x_1},{y_1}} \right)[/latex] and [latex]B[/latex] [latex]\left( {{x_2},{y_2}} \right)[/latex] on the coordinate plane.

By the way, if you already know the skill, you can test your knowledge by working on the practice problems provided.

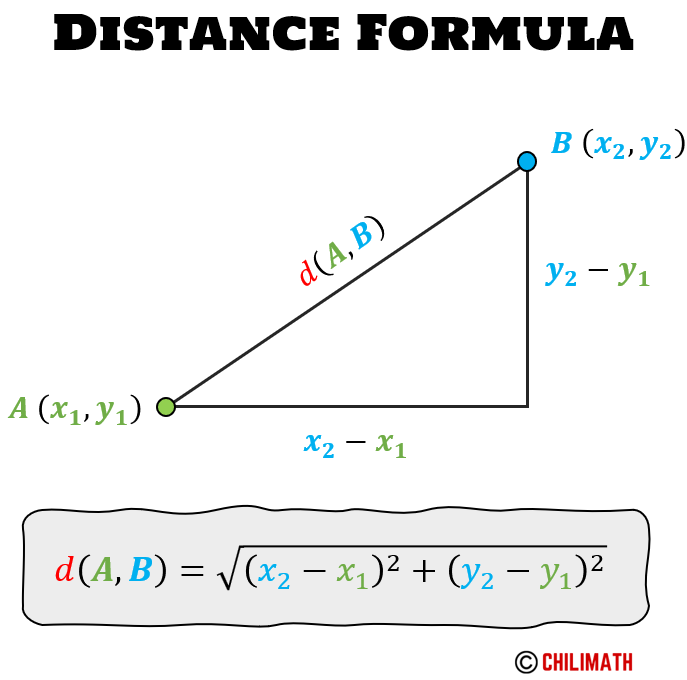
distance between points A and B can be solved by the distance formula which is d(A,B) = sqrt ( (x2-x1)^2+(y2-y1)^2))

The Distance Formula itself is actually derived from the Pythagorean Theorem which is [latex]{a^2} + {b^2} = {c^2}[/latex] where [latex]c[/latex] is the longest side of a right triangle (also known as the hypotenuse) and [latex]a[/latex] and [latex]b[/latex] are the other shorter sides (known as the legs of a right triangle).

The very essence of the Distance Formula is to calculate the length of the hypotenuse of the right triangle which is represented by the letter [latex]c[/latex].

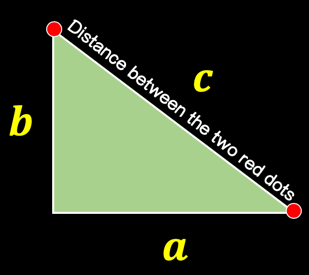
a green right triangle with hypotenuse c (distance between two red dots) and legs a and b.
point A to point B

That’s why we can claim that the idea of the Distance Formula is borrowed and derived from the Pythagorean Theorem. If you want to see how the Distance Formula is derived from the Pythagorean Theorem, please check out my lesson on How to Derive the Distance Formula.

Distance Formula as the Derivative of the Pythagorean Theorem

The distance [latex]d[/latex] between two points

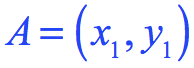
A=(x1,y1)

and

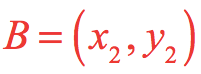
B=(x2,y2)

is calculated or computed using the following formula:

Distance is equal to the square root of the sum of the quantity the square of the difference of x-coordinates and the square of the difference of the y-coordinates. Or in short, d=sqrt[(x2-x1)^2 + (y2-y1)^2].

Below is an illustration showing that the Distance Formula is based on the Pythagorean Theorem where the distance [latex]d[/latex] is the hypotenuse of a right triangle.

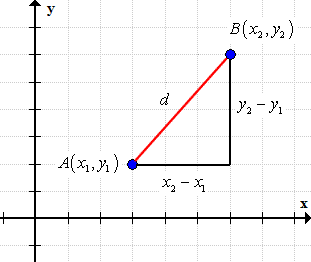
the distance "d" is actually the hypotenuse of the right triangle side where the measures of its legs are (y2-y1) and (x2-x1).

Observations:

a) The expression [latex]{x_2} – {x_1}[/latex] is read as the “change in [latex]x[/latex]”.

b) The expression [latex]{y_2} – {y_1}[/latex] is read as the “change in [latex]y[/latex]”.

On top of the examples below, I have also created additional practice problems for the distance formula which can be found on the link below.

Distance Formula Practice Problems with Answers

Examples of Using the Distance Formula

Below is a list of all the problems in this lesson.

  1. How far is the point [latex](6,8)[/latex] from the origin?
  2. Find the distance between the two points [latex](–3, 2)[/latex] and [latex](3, 5)[/latex].
  3. What is the distance between the two points [latex](–1, –1)[/latex] and [latex](4, –5)[/latex]?
  4. How many units apart are the points [latex](–4, –3)[/latex] and [latex](4, 3)[/latex]? Solve in two different ways and show that the final answer is the same.
  5. Find the radius of a circle with a diameter whose endpoints are [latex](–7, 1)[/latex] and [latex](1, 3)[/latex].
  6. Find the two points of the form [latex]\left( {{\color{red}{x}},-4} \right)[/latex] that have the same distance of [latex]10[/latex] units from the point [latex]\left( {3,2} \right)[/latex].

Example 1: How far is the point (6,8) from the origin?

The origin is the red dot with x-coordinate of [latex]0[/latex] and y-coordinate of [latex]0[/latex]. We can write it in ordered pair as [latex]\color{red}\left( {0,0} \right)[/latex].

While the other point is the blue dot having an x-coordinate of [latex]6[/latex] and y-coordinate of [latex]8[/latex]. Similarly, this can be written as the ordered pair [latex]\color{blue}\left( {6,8} \right)[/latex].

If we plot the points [latex]\color{red}\left( {0,0} \right)[/latex] and [latex]\color{blue}\left( {6,8} \right)[/latex] on a Cartesian Plane, we will get something similar to the one below.

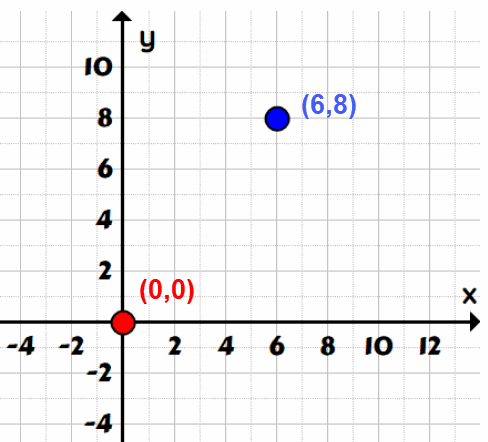
origin is represented by the ordered pair (0,0) while the other point by the ordered pair (6,8)

If we let the origin be the first point, then we have [latex]\left( {{x_1},{y_1}} \right) = \left( {0,0} \right)[/latex] which implies [latex]{x_1} = 0[/latex] and [latex]{y_1} = 0[/latex].

Consequently, the second point would be [latex]\left( {6,8} \right)[/latex]. Therefore, [latex]\left( {{x_2},{y_2}} \right) = \left( {6,8} \right)[/latex] which means [latex]{x_2} = 6[/latex] and [latex]{y_2} = 8[/latex].

Now, we substitute the values into the Distance Formula then simplify to get the distance between the two points in question.

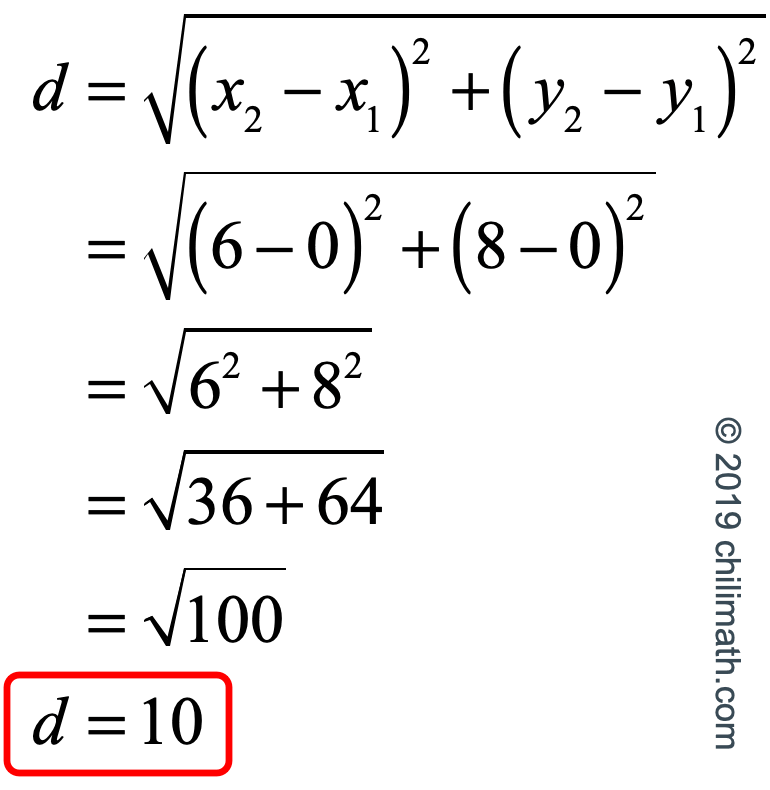
the distance between (0,0) and (6,8) is 10 units

Example 2: Find the distance between the two points (–3, 2) and (3, 5).

Label the parts of each point properly and substitute it into the distance formula.

If we let [latex]\left( { – 3,2} \right)[/latex] be the first point then it will take the subscript of 1, thus, [latex]{x_1} = – 3[/latex] and [latex]{y_1} = 2[/latex].

Similarly, if [latex]\left( {3,5} \right)[/latex] be the second point it will have the subscript of 2, thus, [latex]{x_2} = 3[/latex] and [latex]{y_2} = 5[/latex].

Here is the calculation,

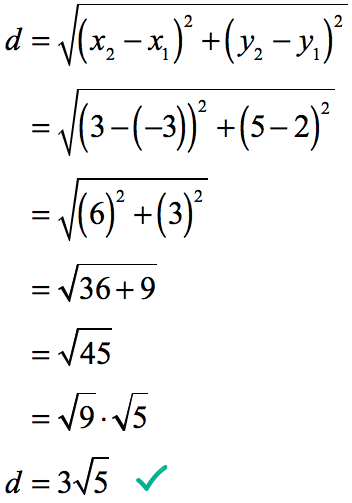
d = square root of = square root of (6^2 + 3^2) = square root of (36 + 9) = square root of (45) = 3 times square root of 5.

Therefore, the distance between two points (–3, 2) and (3, 5) is [latex]3\sqrt 5[/latex] . This is how it looks on a graph.

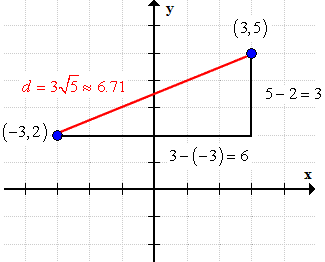
the hypotenuse of the right triangle is 3 times the square root of 5 which is approximate 6.71

Example 3: What is the distance between the points (–1, –1) and (4, –5)?

If we assign [latex]\left( { – 1, – 1} \right)[/latex] as our first point then

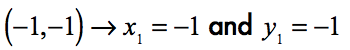
for the point (-1,-1), the x-coordinate is negative 1 (-1) while the y-coordinate is also negative 1 (-1)

In the same manner, assigning [latex]\left( {4, – 5} \right)[/latex] as our second point, we have

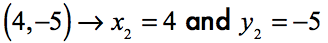
the point (4,-5) has the x-coordinate of positive 4 (+4) and the y-coordinate of negative 5 (-5)

Plugging in the values of [latex]x[/latex] and [latex]y[/latex], we get:

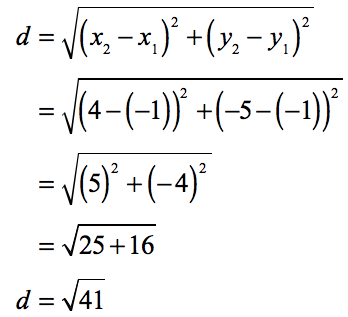
distance is equal to the square root of 41

The two points and the distance between them which is [latex]\sqrt {41}[/latex] can be shown on a graph just like the one below.

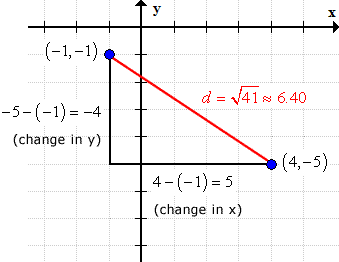
a right triangle with the hypotenuse having endpoints of (-1,-1) and (4,-5). the change in y is -4 while the change in x is 5.

Example 4: How far apart are two points (–4, –3) and (4, 3) from each other? Solve in two different ways and show that the distance is the same.

Sometimes you may wonder if switching the points in calculating the distance can affect the final outcome.

Well, if you think about it, the formula is squaring the difference of the corresponding [latex]x[/latex] and [latex]y[/latex] values. That means it doesn’t matter if the change in [latex]x[/latex], also known as delta [latex]x[/latex], or the change in [latex]y[/latex], also known as delta [latex]y[/latex], is negative because when we eventually square it (raise to the 2nd power), the result always comes out to be positive.

Let’s “prove” that the answer is always the same by solving this problem in two ways!

The first solution shows the usual way because we assign which point is the first and second based on the order in which they are given to us in the problem. In the second solution, we switch the points.

  • Solution 1:
first point is (-4,-2)
second point is (4,3)
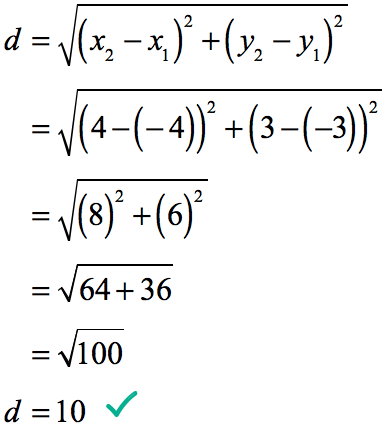
d=sqrt((x2-x1)^2+(y2-y1)^2) = sqrt(8^2+6^2) = 10 units.

[latex]10[/latex] units

  • Solution 2:
the second point becomes the first point which is now (4,3) from (-4,-3)
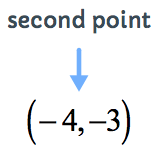
the first point becomes the second point which is now (-4,-3) from (4,3)
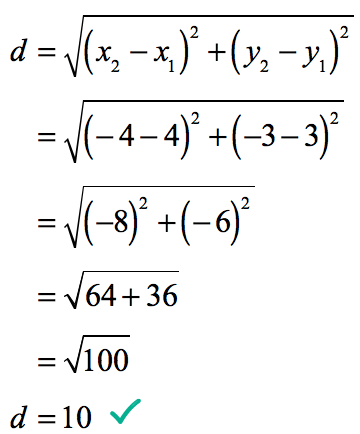
d = sqrt = sqrt = sqrt (64 + 36) = sqrt(100) = 10.

[latex]10[/latex] units

As you can see, both solutions arrived at the same answer or result which is the distance of [latex]10[/latex], [latex]d = 10[/latex]. Below is the visual solution to the problem.

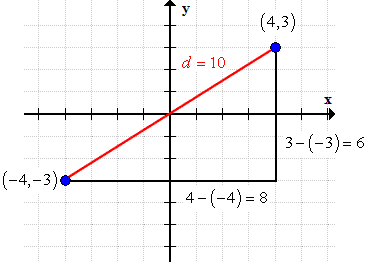
the distance between the two points is the hypotenuse where d=10.

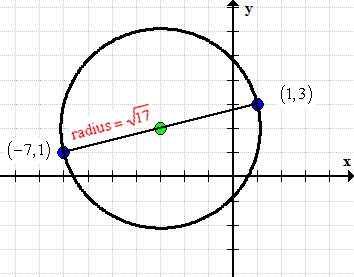
Example 5: Find the radius of a circle with a diameter whose endpoints are (–7, 1) and (1, 3).

Remember that the diameter of a circle is twice the length of its radius. If that’s the case, then the radius is half the length of the diameter.

r = (1/2)d where r is the radius while d is the diameter

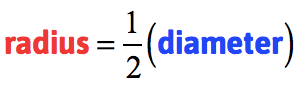
Here’s the plan! Since we are given the endpoints of the diameter, we can use the distance formula to find its length. Finally, we divide it by 2 to get the length of the radius, as required by the problem.

  • Find the length of the diameter with endpoints [latex]\left( { – 7,1} \right)[/latex] and [latex]\left( {1,3} \right)[/latex].
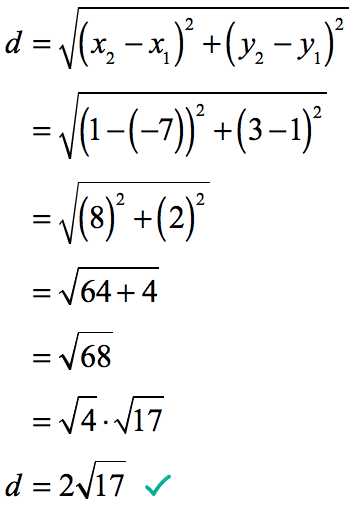
d = 2 sqrt(17)
  • Solve for the radius by dividing the diameter by [latex]2[/latex].
radius = (1/2) [2 sqrt(17)] = sqrt(17).
  • The blue dots are the endpoints of diameter and the green dot is the center of the circle (calculated using the midpoint formula) located at [latex]\left( { – 3,2} \right)[/latex].
the circle with a center of (-3,2), with endpoints of the diameter of (-7,1) and (1,3), and with a radius as solved before as sqrt(17)

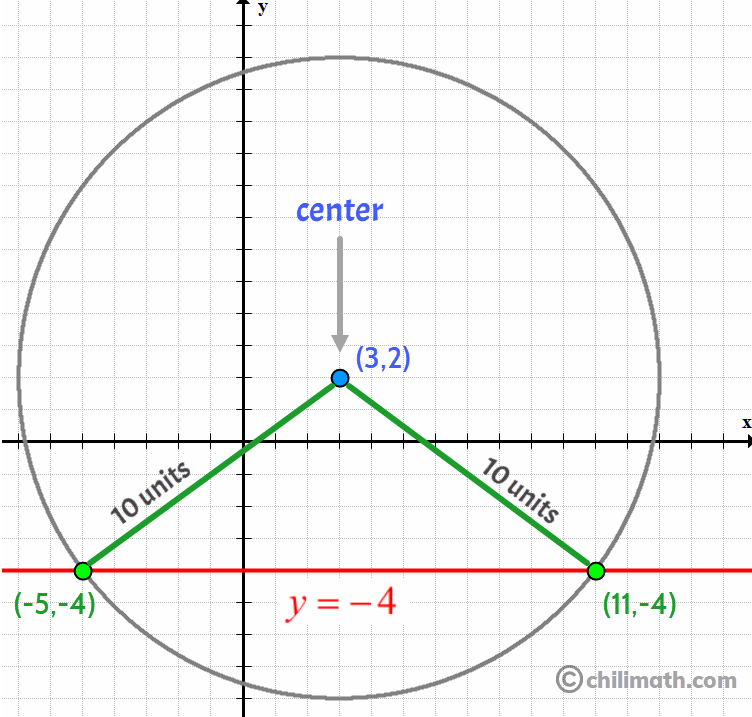
Example 6: Find the two points of the form [latex]\left( {{\color{red}{x}},-4} \right)[/latex] that have the same distance of [latex]10[/latex] units from the point [latex]\left( {3,2} \right)[/latex].

This problem is slightly different. Notice that one point, namely [latex]\left( {x, – \,4} \right)[/latex], contains the variable [latex]\large\color{red}x[/latex] instead of a specific number.

I suggest that you approach this just the same as the previous problems. Now, assign which of the points will be the first and second, that is, [latex]\left( {{x_1},{y_1}} \right)[/latex] and [latex]\left( {{x_2},{y_2}} \right)[/latex], respectively. Then substitute the values into the formula and solve.

In this case, you will see immediately that you won’t get a value as the distance. Instead, you will have to solve a quadratic equation to obtain two numbers. Be careful here. Either of the two numbers doesn’t represent a distance. The two numbers will be the x-coordinates of two points. Remember that x-coordinate is always the first value of the ordered pair [latex]\left( {{\color{red}{x}},y} \right)[/latex]

It’s up to you to designate which one is going to be the first point, therefore forcing the other point to be the second.

It’s doesn’t matter which of the two points you select as the first or second point because the outcome will always be the same as shown in Example #4.

Remember, the Distance Formula is constructed as follows:

  • the second x-coordinate subtracted by the first x-coordinate
  • the second y-coordinate subtracted by the first y-coordinate

It makes sense for us to let the point [latex]\left( {{\color{red}{x}},-4} \right)[/latex] be the second point while [latex]\left( {3,2} \right)[/latex] be the first point.

By doing so, we will have a situation where the variable [latex]\color{red}x[/latex] is being subtracted by the number [latex]3[/latex]. Thus, [latex]x-3[/latex]. This is great because the coefficient of the variable [latex]\color{red}{x}[/latex] is positive.

1st point is (3,2) which implies x1=3 and x2=2 while 2nd point is (x,-3) which implies x2=x and y2=-4

Don’t forget that the two points have the same distance of [latex]10[/latex] units from [latex](3,2)[/latex].

We substitute the values above into the Distance Formula below then simplify.

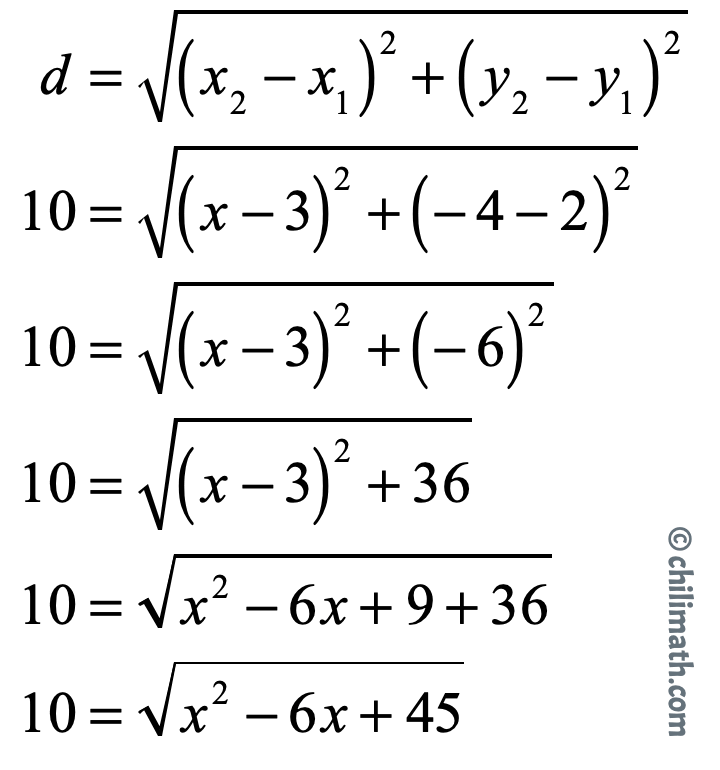
10=sqrt(x^2-6x+45)

Now, square both sides of the equation to get rid of the square root symbol on the right side. Next, subtract both sides by [latex]100[/latex] to make the left side equal to [latex]0[/latex]. Finally, factor out the trinomial on the right side then set each factor equal to [latex]0[/latex] to solve for [latex]x[/latex].

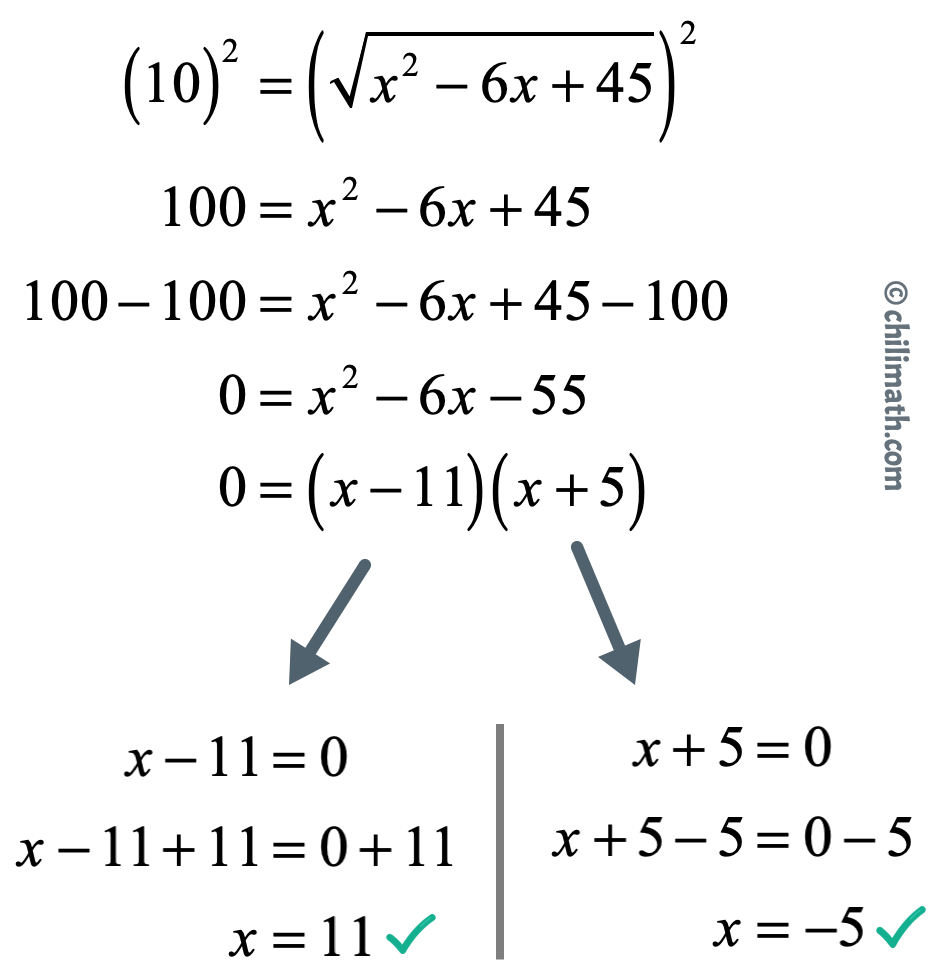
0=(x-11)(x+5)

Therefore, the two points [latex]\left( {{\color{red}{11}},-4} \right)[/latex] and [latex]\left( {{\color{red}{-5}},-4} \right)[/latex] both have the same distance of [latex]\color{blue}10[/latex] units from the point [latex]\left( {3,2} \right)[/latex].

I will leave it to you to verify that the distance between [latex]{\left( {11, – \,4} \right)}[/latex] and [latex]{\left( {3,2} \right)}[/latex], and between [latex]{\left( { – 5, – \,4} \right)}[/latex] and [latex]{\left( {3,2} \right)}[/latex] are both [latex]10[/latex] units.

graph showing a circle centered at (3,2) and two radii with length 10 units going to the points on the circle (-5,-4) and (11,-4)

You may also be interested in these related math lessons or tutorials:

Distance Formula Practice Problems with Answers

Derivation of the Distance Formula

Distance between Point and Line Formula

Midpoint Formula