The Midpoint Formula

Think of the midpoint as the “halfway” or middle point of a line segment. This so-called center point divides the line segment into two equal or congruent parts.

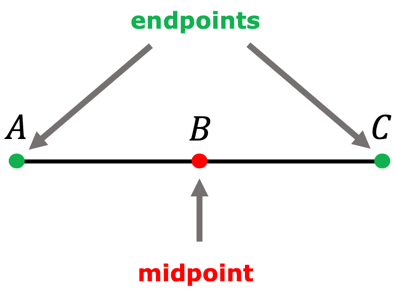
NOTE: The midpoint of line segment [latex]AC[/latex] denoted by the symbol [latex]\overline {AC} [/latex] is located at point [latex]B[/latex]. This implies that line segment [latex]AB[/latex], written as [latex]\overline {AB} [/latex], and line segment [latex]BC[/latex], written also as [latex]\overline {BC} [/latex], have equal measure. Therefore, [latex] \overline {AB} = \overline {BC} [/latex].

---

In a nutshell, the formula to find the midpoint of two given points is the following.

The Midpoint Formula

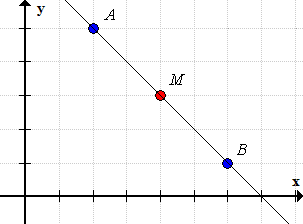
The midpoint M of the line segment with endpoints [latex]A\left( {{x_1},{y_1}} \right)[/latex] and [latex]B\left( {{x_2},{y_2}} \right)[/latex] is calculated as follows:

Observations:

a) The [latex]x[/latex]-coordinate of the midpoint is the average of the [latex]x[/latex]-values from the given points. That means add the x-coordinates then divide by [latex]2[/latex].

b) The [latex]y[/latex]-coordinate of the midpoint is the average of the [latex]y[/latex]-values from the given points. That means add the y-coordinates then divide by [latex]2[/latex].

---

Examples on How to Use the Midpoint Formula

Let’s go over five (5) different examples to see the midpoint formula in action!

Example 1: Find the midpoint of the line segment joined by the endpoints [latex](–3, 3)[/latex] and [latex](5, 3)[/latex].

When you plot the points in the xy-axis and join them with a ruler, the line segment is obviously horizontal because the y-coordinates of points are equal. In doing so, it is easy to approximate or guess the midpoint even without the midpoint formula. You can do just that by counting the same number of units from both sides of the endpoints until it reaches the center.

Remember the x-coordinate of the midpoint is the average of the x-coordinates of the endpoints. Similarly, the y-coordinate of the midpoint is the average of the y-coordinates of the endpoints.

However, let’s work it out using the formula to find the midpoint.

Let [latex](–3, 3)[/latex] be the first point so [latex]{x_1} = – 3[/latex] and [latex]{y_1} = 3[/latex]. In the same manner if [latex](5, 3)[/latex] is the second point then [latex]{x_2} = 5[/latex] and [latex]{y_2} = 3[/latex].  Substitute these values in the formula, and simplify to get the midpoint.

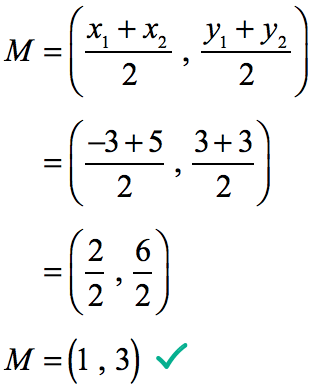
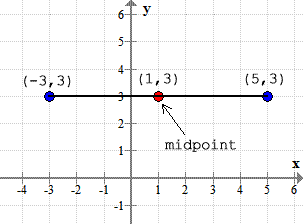
Therefore, the midpoint of the horizontal line segment is [latex](1,3)[/latex].

Here are the points plotted in the Cartesian plane, together with the calculated value of the midpoint.

---

Example 2: Find the center point of a line segment with endpoints [latex](1, 5)[/latex] and [latex](1, –1)[/latex] using the midpoint formula.

This particular line segment is clearly vertical because the two points have the same [latex]x[/latex]-coordinates. More so, plotting the points in the xy-axis verifies the case. Like in our previous example, the midpoint of this vertical line segment can easily be approximated by counting the same number of units from both sides of the endpoints.

Anyway, let’s solve this using the formula.

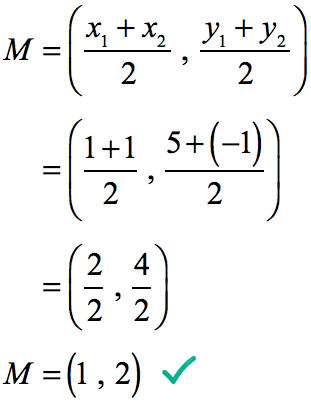
Therefore, the midpoint of the vertical line segment is [latex](1,2)[/latex].

Here’s how it looks on the graph.

---

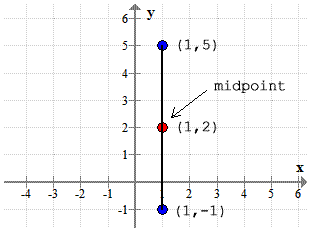
Example 3: Determine the midpoint of a line segment whose endpoints have coordinates [latex](–4, 5)[/latex] and [latex](2, –3)[/latex].

Notice that when you plot the line segment generated by the given endpoints, the resulting line segment is neither horizontal nor vertical, unlike the last two examples. You instead get a diagonal line segment. So technically, you will find the midpoint of a diagonal line segment. This time around, it is more difficult to guess or approximate the midpoint. However, with the use of the formula, this should not be a problem.

We can let [latex]\left( {{x_1},{y_1}} \right) = \left( { – 4,5} \right)[/latex] and [latex]\left( {{x_2},{y_2}} \right) = \left( {2, – 3} \right)[/latex].

Now, substitute and evaluate the values in the midpoint formula.

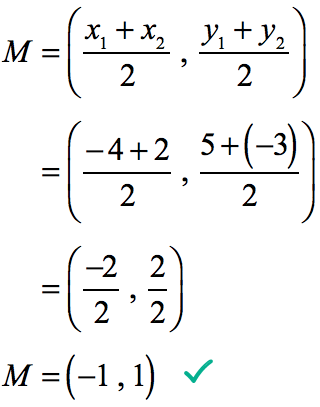
Therefore, the midpoint of the diagonal line segment is [latex](-1,1)[/latex].

Here’s the graph.

---

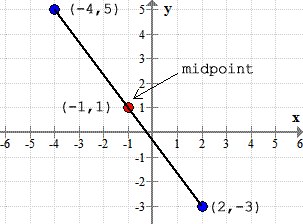
Example 4: Find the missing value of [latex]h[/latex] in the points [latex](5, 7)[/latex] and [latex](1, h)[/latex] if its midpoint is at [latex](3, -2)[/latex].

Since the midpoint is actually given to us, start by setting the formula equal to the numerical value of the midpoint. Just like this.

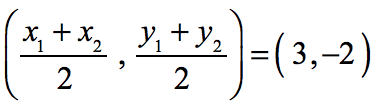
We let [latex]\left( {{x_1},{y_1}} \right) = \left( {5,7} \right)[/latex] and [latex]\left( {{x_2},{y_2}} \right) = \left( {1,h} \right)[/latex]. Then substitute these values in the formula.

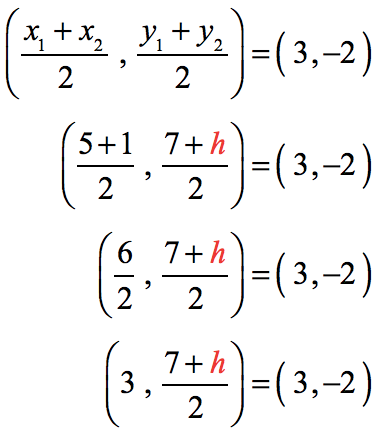
If you observe, two points are equal whenever their corresponding coordinates are the same. That is, the [latex]x[/latex]-values are equal, and the [latex]y[/latex]-values are equal as well.

Notice, that the [latex]x[/latex]-values are both equal to 3. Great!

But we want to do the same thing with the [latex]y[/latex]-coordinates by setting them equal to each other. By doing so, we created a simple equation that can be solved for the missing value of [latex]h[/latex].

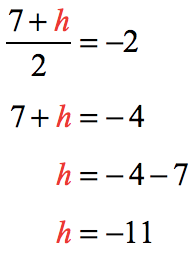
Therefore, the final answer is [latex]h=-1[/latex].

---

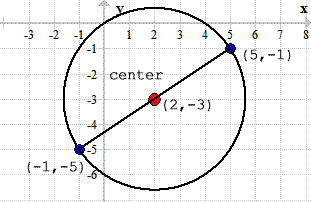
Example 5:  Find the center of a circle whose diameter has endpoints [latex](–1, –5)[/latex] and [latex](5, –1)[/latex].

If you think about it, the center of a circle is just the midpoint of the diameter. This problem is simply reduced to solving the midpoint of the line segment with endpoints [latex](–1, –5)[/latex] and [latex](5, –1)[/latex].

I am sure that you already know how to do this. Just a word of caution though, be very careful when adding or subtracting numbers with the same or different signs. This is where silly mistakes happen because students tend to “relax” when performing basic arithmetic operations. So don’t be.

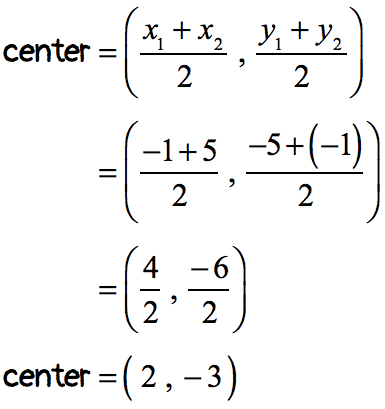
Therefore, the center of the circle is located at [latex](2,-3)[/latex].

Here’s the graph of the circle showing its diameter and center.

---

You may also be interested in these related math lessons or tutorials:

Distance Formula