How to Find the Distance of a Point from a Line
There are a few ways to find the distance between a point and a line. But the easiest of all is through the use of a formula. The derivation of the formula is reserved for another lesson.
The word “distance” here pertains to the shortest distance between the fixed point and the line. This is precisely what the formula calculates – the least amount of distance that a point can travel to any point on the line. In addition, this distance which can be drawn as a line segment is perpendicular to the line.
This concept of perpendicular distance as the shortest distance between a point and a line is best explained using an illustration.
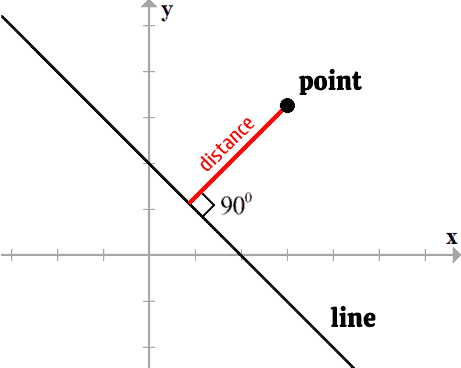
Formula of the Distance between Point and Line
The distance [latex]\large{d}[/latex] between the point with coordinates [latex]\large{\left( {{x_0},{y_0}} \right)}[/latex], and the line written in the general form [latex]\large{ax + by + c = 0}[/latex] is calculated as follows.
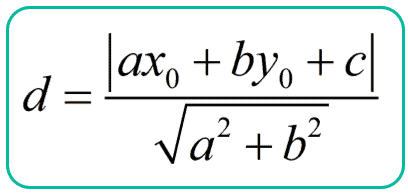
Notice that the values of the coordinates of the point go to the numerator.
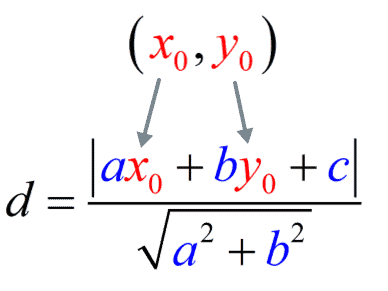
Also, the values of the coefficients of the line written in general form go to the numerator and denominator.
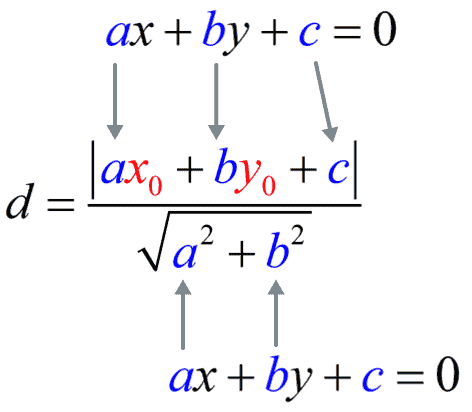
In addition, the numerator has an absolute value symbol which means the numerator will either have a value of zero or a positive number. Thus, the numerator will never be a negative number. The denominator will also be positive since both [latex]\large{a}[/latex] and [latex]\large{b}[/latex] are being squared before they are added.
Examples of the Distance between a Point and a Line
Example 1: Find the distance between the point [latex](0,0)[/latex] and the line [latex]3x + 4y + 10 = 0[/latex].
We have the point [latex](0,0)[/latex] that means [latex]{x_0} = 0[/latex] and [latex]{y_0} = 0[/latex]. Our line is already in the general form so we can easily identify the values for [latex]\large{a}[/latex], [latex]\large{b}[/latex], and [latex]\large{c}[/latex].
From [latex]3x + 4y + 10 = 0[/latex], we have
[latex]\large{a=3}[/latex]
[latex]\large{b=4}[/latex]
[latex]\large{c=10}[/latex]
Since we all have the values needed to be substituted into the formula, we can now calculate the distance between the point [latex](0,0)[/latex] and the line [latex]3x + 4y + 10 = 0[/latex].
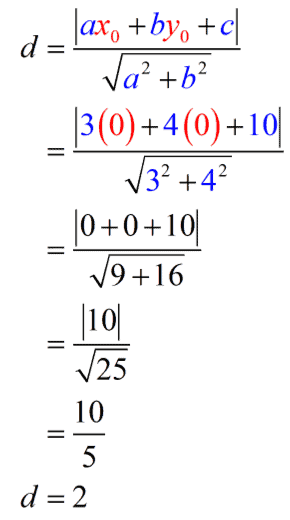
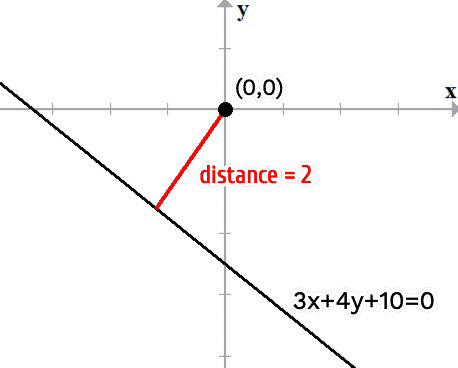
Here’s the diagram of the point and line with a red line segment showing the distance between them.
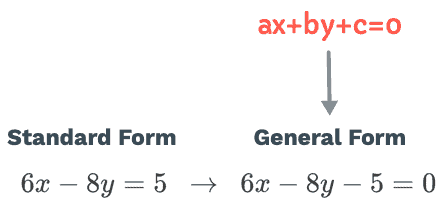
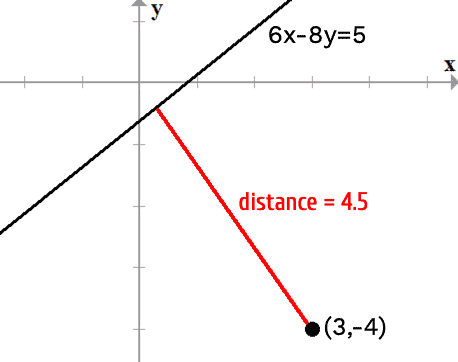
Example 2: Find the distance between the point [latex](3,-4)[/latex] and the line [latex]6x-8y=5[/latex].
The given point is [latex](3,-4)[/latex] thus [latex]{x_0} = 3[/latex] and [latex]{y_0} = -4[/latex]. But the line [latex]6x-8y=5[/latex] is written in standard form. We need to convert it to general form by subtracting both sides of the equation by [latex]5[/latex].
From [latex]6x – 8y – 5 = 0[/latex]
[latex]\large{a=6}[/latex]
[latex]\large{b=-8}[/latex]
[latex]\large{c=-5}[/latex]
We have all the values needed to calculate the distance between the point and the line.
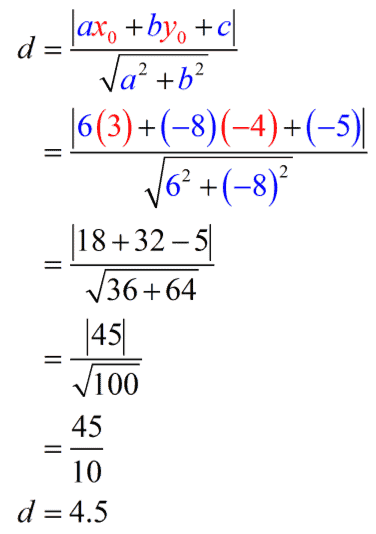
Here is the illustration showing the distance between the point [latex](3,-4)[/latex] and the line [latex]6x-8y=5[/latex]. The red line segment is the length of the distance.
Example 3: Find the distance between the point [latex](10,5)[/latex] and the line [latex]{y = {\Large{5 \over 3}}x + 7}[/latex].
From the given point, we know that [latex]{x_0} = 10[/latex] and [latex]{y_0} = 5[/latex]. However for the line, it is not written in the form that we want.
The given line [latex]{y = {\Large{5 \over 3}}x + 7}[/latex] is expressed in the Slope-Intercept Form. We need to rewrite it into the general form [latex]ax + by + c = 0[/latex].
We can do that by multiplying both sides of the equation by [latex]3[/latex]. Then, we subtract both sides by [latex]5x[/latex]. Finally, subtract both sides by [latex]21[/latex].
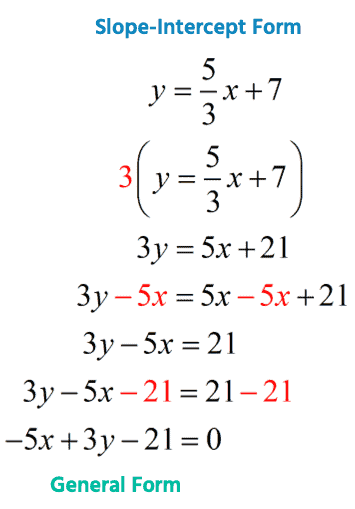
We have all the necessary information to compute for the distance between the given point and line.
► From the point [latex](10,5)[/latex], we have
[latex]{x_0} = 10[/latex] and [latex]{y_0} = 5[/latex]
► From the line [latex] – 5x + 3y – 21 = 0[/latex], we have
[latex]\large{a=-5}[/latex]
[latex]\large{b=3}[/latex]
[latex]\large{c=-21}[/latex]
Thus,
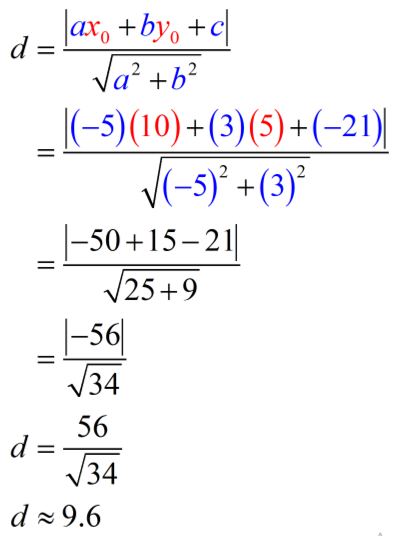
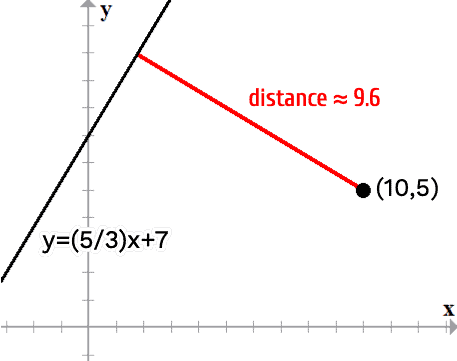
Below is the diagram showing the point [latex](10,5)[/latex], line [latex]{y = {\Large{5 \over 3}}x + 7}[/latex], and its perpendicular distance.
You may also be interested in these related math lessons or tutorials:
