Perimeter of a Square Formula
A square’s perimeter is the distance around its boundary or edges. When you trace the edges of a chess board with your finger, the distance traveled by your finger around all four sides of the chess board is an example of a square’s perimeter. The perimeter of a square can be calculated by adding the lengths of all four sides or by simply multiplying the length of one of its sides by 4.
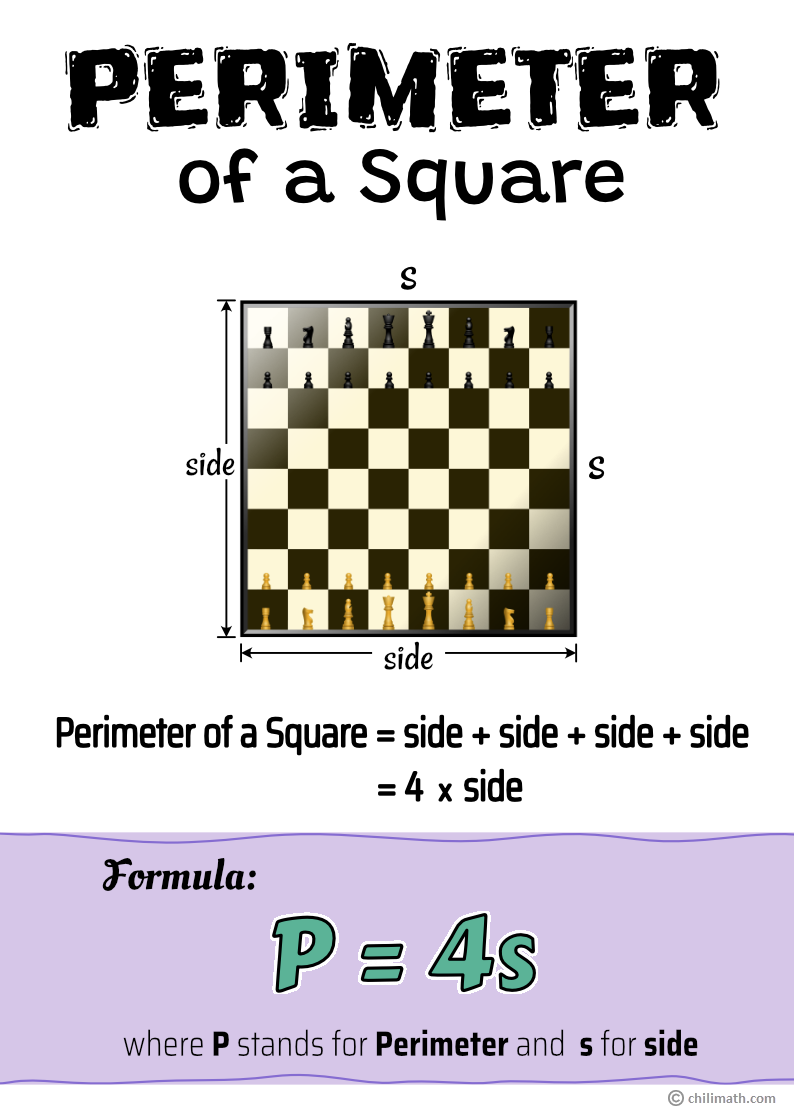
How to Find the Perimeter of a Square
A square is probably the easiest geometrical shape to draw as it is only made up of four line segments of equal length. A square, in other words, has four sides that are congruent and it also has four right angles.
Note: The number of tick marks indicates congruent sides.
Finding the perimeter of a square is similar to a rectangle where we get the sum of the lengths of all its sides. But, since all four sides of a square have the same measurement, we will not have separate measurements for the length and the width. All we need to do is add up all four sides of the square. The equation looks like this:
[latex]P = side + side + side + side[/latex]
where [latex]P[/latex] stands for perimeter and [latex]s[/latex] for side
However, since repeated addition can also be written in the form of multiplication, we can simply multiply the side length by [latex]4[/latex] or write is as [latex]P = 4 \times side[/latex] or [latex]P = 4s[/latex].

Finding the Perimeter of a Square Examples
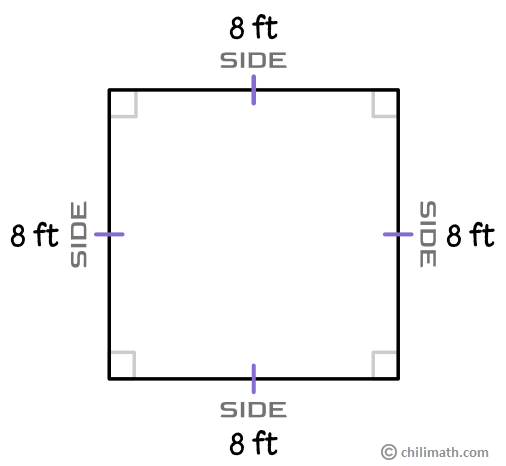
Example 1: Find the square’s perimeter.

In the illustration above, we are given a square with a side length of 13 meters. Even though it only shows the measurement on one side, we know that all the other sides also measure 13 meters because a square has congruent sides.
To find its perimeter, let’s use the formula and substitute the side ([latex]s[/latex]) with its given measurement which is 13 meters.
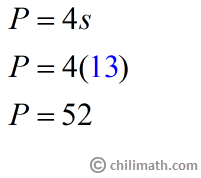
The square’s perimeter is 52 meters.
Example 2: The perimeter of the square below is 108 inches. What is the measurement of its sides?
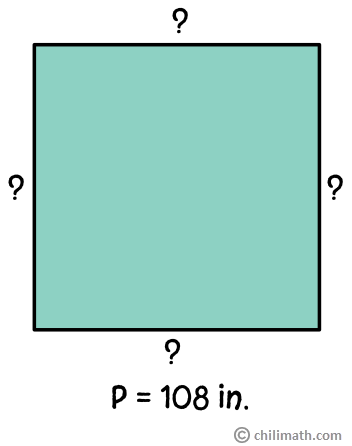
This next problem is asking us to find the side lengths of the square given its perimeter. We can still use the formula for a square’s perimeter to find the missing side measure. This time, however, we will substitute [latex]P[/latex] with the value of our perimeter which is 108 inches then solve for the side ([latex]s[/latex]).
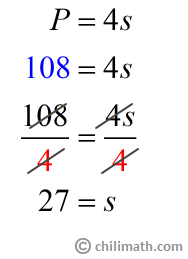
Great! Now we know that one side of the square measures 27 inches. But since all four sides of the square are of equal measure, this also means that each of the other three sides also has a length 27 inches.
Check:
To check if we got the correct answer, we simply have to multiply 27 in. by 4 (since the square has four sides). If the result matches our perimeter of 108 in., then that means we got the correct side measurement.
[latex]27(4) = 108[/latex]
And we did! Therefore, each side of the square measures 27 inches.
Example 3: If the side lengths of the square below are decreased by 3 centimeters, what is the perimeter of the new square?
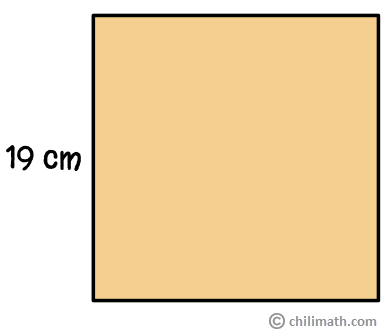
Decreasing each side length means that we need to subtract 3 cm from our current side measurement which is 19 cm. So, we have [latex]19 – 3 = 16\,cm[/latex] as the length of each side of the new square.
Let’s proceed by calculating the perimeter using the formula.
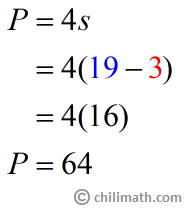
The perimeter of the new square is 64 centimeters.
Example 4: Each table napkin at our favorite Mexican restaurant measures 14.5 inches on all sides. What is the perimeter of each napkin?

Since we are told that all four sides of each table napkin measures 14.5 inches, we can easily tell that its shape is a square. We can then find its perimeter using the formula for a square’s perimeter.

The perimeter for each table napkin is 58 inches.
Example 5: A square-shaped playground has length of 40 feet on each side. The town mayor wants to expand its size by adding 7 feet on each side then put a fence around it. How many feet of fencing will they need for the expanded playground?

Remember that perimeter is the total length or distance around the boundary of a two-dimensional shape. Therefore, the fencing that will enclose all sides of the expanded playground represents its perimeter.
Before we do any calculations, let’s first identify the information available to us. If you’re a visual person like me, it’s often helpful drawing it out.
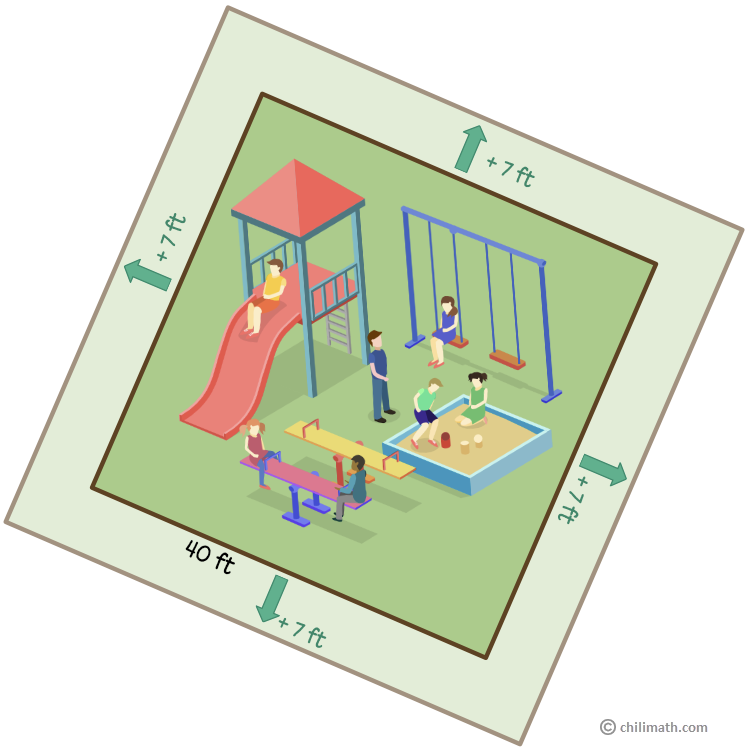
Off the bat, we know that the side lengths of the expanded playground will now be 47 ft by simply adding 7 ft to the current side measurement of 40 ft.
Let’s go ahead and find the perimeter of the expanded playground using the perimeter of a square formula.

Hence, they will need 188 feet of fencing for the expanded playground.
Example 6: The area of a square is 64 square inches. Find its perimeter.
We know the area of the square to be the square of its side, that is, [latex]A=s^2[/latex]. That means its side is simply [latex]8[/latex] inches because
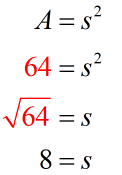
Since we found the side of the square to be [latex]s=8[/latex], we can calculate the perimeter using the formula [latex]P=4s[/latex].
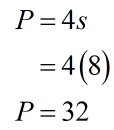
Therefore, a square with an area of [latex]64[/latex] square inches has a perimeter of [latex]32[/latex] inches.
You may also be interested in these related math lessons or tutorials:
