Area of a Rectangle Formula
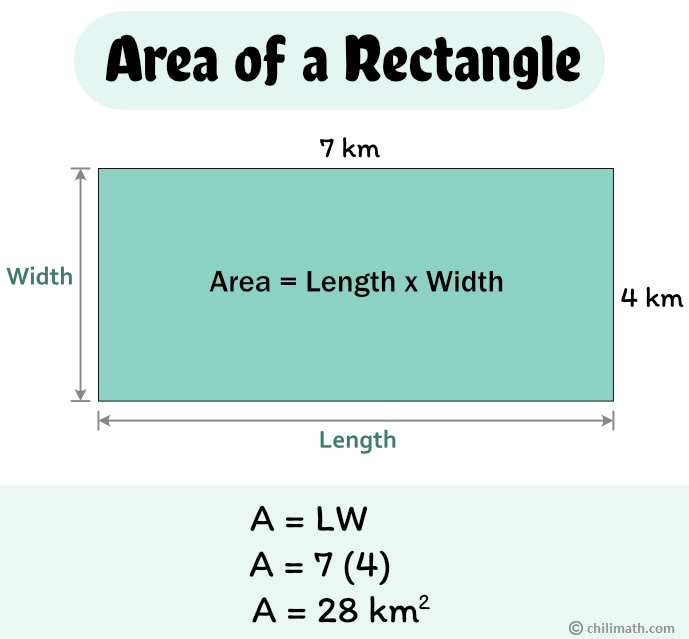
The area of a rectangle is the amount of space inside the rectangle. We can find the area of a rectangle by multiplying the length of the rectangle by its width.
Measuring the Area using Unit Squares
But before we delve into the formula, let’s touch quickly on what an area of a rectangle is. Area as we know is measured in square units. So when we talk about the area, we also pertain to the number of equal-sized square units that the rectangle encloses or the number of equal-sized square units needed to fill the flat surface of the rectangle or of any two-dimensional shape. We write the area in units squared or units2.
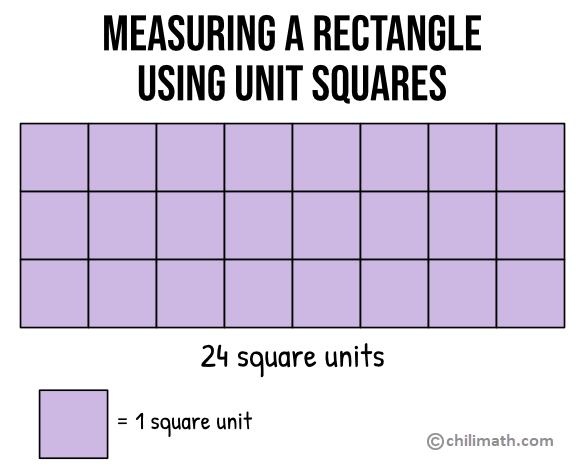
In the illustration above, we are able to fit 24 square units inside the rectangle. So if the area of each unit square is 1 foot2, then we can say that the area of the rectangle is 24 square feet2.
Let’s say you have a rectangular kitchen, and you want to replace the floor tiles. Wouldn’t it be helpful to know how many square tiles you need to cover the entire floor space in your kitchen before you start making a purchase? However, trying to measure the floor one tile at a time is time-consuming and just not practical. So this is where the formula for finding the area becomes very useful.
How to Find the Area of a Rectangle
The formula for finding the area of the rectangle is

Let’s now apply this formula to the given rectangle below with a length of 8 feet and a width of 3 feet.
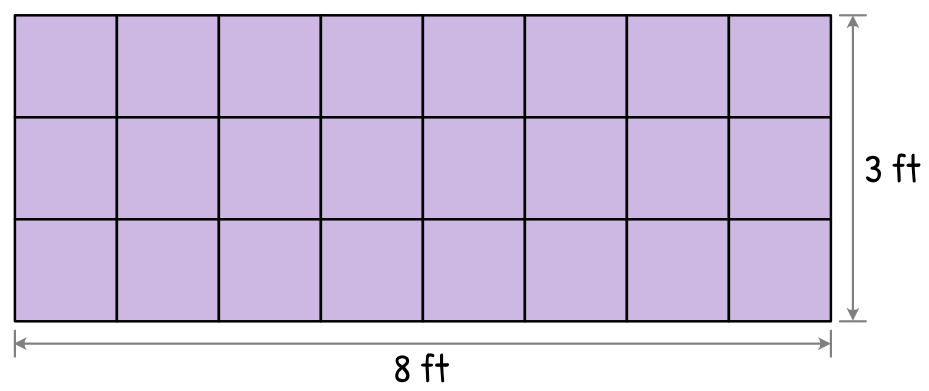
Using the formula to find the area of a rectangle
[latex]A = LW[/latex]
[latex]A = 8\left( 3 \right)[/latex]
[latex]A = 24 f{t^2}[/latex]
We get an answer of 24 ft2 which also means that 24 square units, each with an area of 1 ft2 can fit inside the rectangle.
Finding the Area of a Rectangle Examples
Let’s now tackle some problems that involve finding the area of a rectangle.
Example 1: Find the area of the rectangle.

Let’s begin by identifying the pieces of information that are available to us. Here we are given the measurement of the rectangle’s length ([latex]L[/latex]) and width ([latex]W[/latex]).
[latex]L = 29\,in[/latex]
[latex]W = 16\,in[/latex]
To find the area of the rectangle, we simply have to multiply the length of the rectangle by its width. Hence the area formula,
[latex]\textbf{\textit{A = LW}}[/latex]
[latex]A = 29\left( {16} \right)[/latex]
[latex]A = 464 \,i{n^2}[/latex]
The area of the rectangle is 464 in2.
Example 2: If the area of the rectangle below is 187 m2, what is the measure of its length?
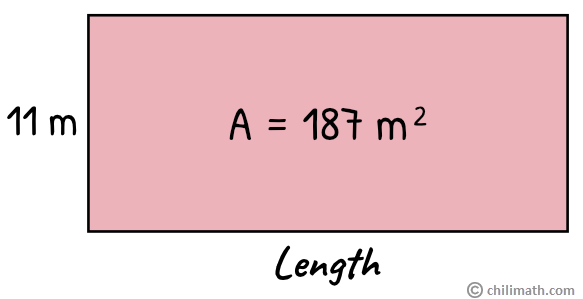
In this problem, rather than finding the rectangle’s area, we are asked to find the length instead. We can still use the area of a rectangle formula to determine how long the rectangle is.
[latex]\textbf{\textit{A = LW}}[/latex]
[latex]187 = L(11)[/latex]
[latex]\Large{{187} \over {11}} = {{11L} \over {11}}[/latex]
[latex]17 = L[/latex] or [latex]L = 17 \,m[/latex]
So we got the measurement of the length as 17 m. But you know that in math, it’s always good to verify your answer to make sure that it is correct. Let’s see if we’ll get the same area if we multiply the length by the width.
Check:
[latex]A = LW[/latex]
[latex]187\,{m^2} = 17m\, \cdot \,11m[/latex]
[latex]187\,{m^2} = 187\,{m^2}[/latex]
And we do! Therefore, the length of the rectangle is 17 meters or 17 m.
Example 3: Mr. Johnson decides to fence a plot of land on his ranch. The plot of land has an area of 414 m2. How wide is the plot of land if it is 23 meters long?
So we can get a better picture of the plot of land that Mr. Johnson wants to fence in, let’s draw it out with the pieces of information given to us.

Just like in our previous example, we will find the measurement of the rectangle’s width by substituting the given value of the area and length into the area of rectangle formula, then solve for the width ([latex]W[/latex]).
[latex]A = LW[/latex]
[latex]414 = 23W[/latex]
[latex]\Large{{414} \over {23}} = {{23W} \over {23}}[/latex]
[latex]18 = W[/latex] or [latex]W = 18 \,m[/latex]
And what is 23 m multiplied by 18 m? Yes, you got it right! Both dimensions, when multiplied together, will give us an area of 414 m2.
So, Mr. Johnson’s plot of land is 18 meters or 18 m wide.
Example 4: Elijah wants to paint a wall in his bedroom. The wall is 18 feet long and 15 feet wide. If he can paint 90 ft2 of the wall with one can, how many cans of paint will he need to paint the entire wall?
Let’s start again by drawing the wall using the dimensions given to us in the word problem.
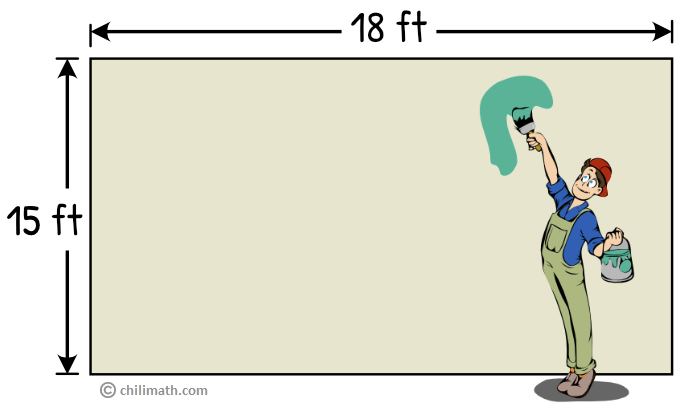
But before we can determine how many cans of paint he needs to paint the entire wall, we first need to find the area of the wall. Since we are given the length and the width, this would be easy!
[latex]A = LW[/latex]
[latex]A = 18 \cdot 15[/latex]
[latex]A = 270\,f{t^2}[/latex]
Now that we know the area of the rectangular wall, we can proceed to divide the total wall area by 90 ft2, which is the area that one can of paint would cover. In doing so, we will be able to determine how many cans Elijah needs to paint the entire wall.

Elijah needs three (3) cans of paint to paint the wall in his bedroom.
Example 5: Cindy and her friends painted a sheet of plywood that was 95 inches long and 48 inches wide for the festival parade. One can of paint covered 1,140 in2 of the plywood. If one can of paint costs $15.25, how much money did Cindy and her friends spend to paint the whole sheet of plywood?
This word problem is somewhat similar to our previous example. Here we are also given the measurements of the length and the width, which will help us find the area easily. But be mindful that it will take extra steps before we get to the exact answer that we are looking for. We need to find the area first and then do another calculation before we can find out what the total cost was to paint the entire sheet of plywood.
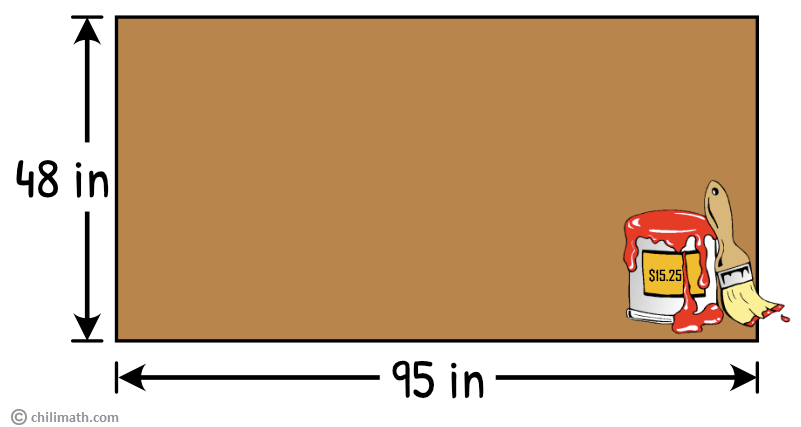
Step 1: Let’s find the area first.
[latex]A = LW[/latex]
[latex]A = 95 \cdot 48[/latex]
[latex]A = 4,560\,\,i{n^2}[/latex]
Now that we know the area of the sheet of plywood, let’s look next at what other pieces of information are given to us in the problem. It says that one (1) can of paint covered 1,140 in2 of the plywood.
Step 2: Therefore, our next step should be to divide the total area of the plywood by the area that a can of paint covers. In doing so, we will be able to find out how many cans of paint were used to paint the entire sheet.

Perfect, we’re on the right track! So Cindy and her friends used four (4) cans of paint to paint the entire sheet of plywood. How much did it cost in total? Well, we know that one can of paint costs $15.25, so
Step 3:
Cost per Can of Paint x Cans of Paint Used = [latex]\$ 15.25\,(4)[/latex]
Total Cost of Paint = [latex]\$ 61.00[/latex]
Cindy and her friends spent $61.00 to paint the whole sheet of plywood for the festival parade.
Example 6: What is the area of the composite figure?
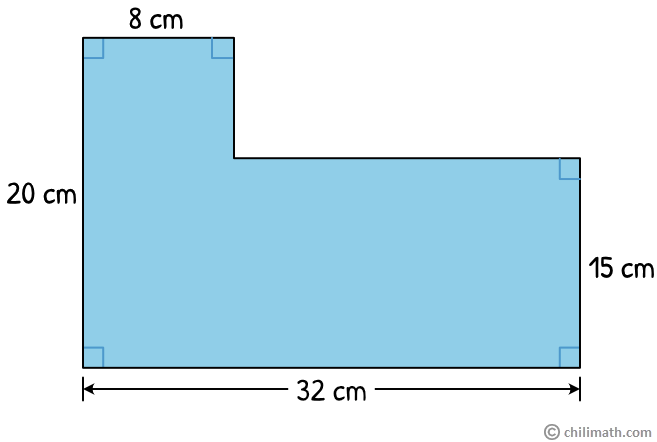
Finding the total area of a composite figure may look intimidating at first glance. However, a composite figure is nothing but two figures or shapes combined or put together. Hence, they are also sometimes called “combined figures.” To find its total area, we simply have to separate the two figures by merely drawing a line and calculating the area for each one.
In this example, our composite figure is composed of two rectangles. Let’s separate them so we can find the area for each one.
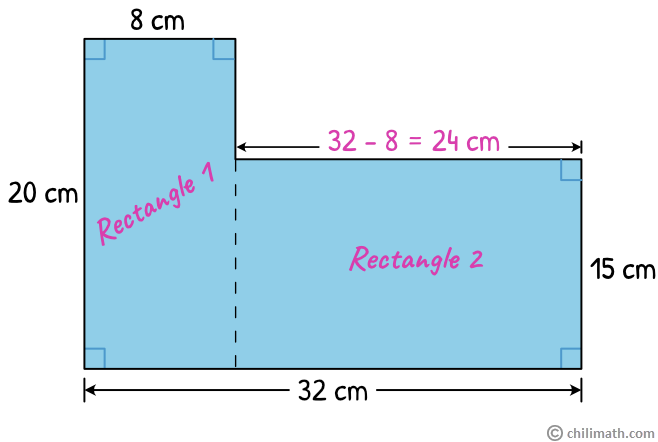
- Rectangle 1
[latex]A = LW[/latex]
[latex]A = 20 \cdot 8[/latex]
[latex]A = 160\,c{m^2}[/latex]
- Rectangle 2
[latex]A = LW[/latex]
[latex]A = 24 \cdot 15[/latex]
[latex]A = 360\,c{m^2}[/latex]
Now that we have the areas for Rectangle 1 and Rectangle 2, we are ready to find the total area of the composite figure. We simply have to add the two separate areas.
Area of Rectangle 1 + Area of Rectangle 2 = Total Area of Composite Figure
[latex]160\,c{m^2} + 360\,c{m^2} = 520\,c{m^2}[/latex]
The total area of the composite figure is 520 cm2.
Example 7: The area of a rectangular pool is 392 ft2. If its length is twice its width, what are the dimensions of the rectangular pool?
This problem is quite unique because we are given the area of the rectangular pool, but the measurement of its length is expressed in a math phrase – which means it needs to be translated into an algebraic expression first before we can start finding the dimensions of the pool.
- Step 1: Since our length has been expressed in terms of the width, we’ll start with finding the value of our width. We begin by using our formula for finding the area of a rectangle. Since the area is already known, we’ll substitute it into the equation and use the width ([latex]W[/latex]) as our unknown variable.
[latex]A = LW[/latex]
[latex]392 = (2W)(W)[/latex]
[latex]392 = 2{W^2}[/latex]
[latex]\Large{{392} \over 2} = {{2{W^2}} \over 2}[/latex]
[latex]196 = {W^2}[/latex]
[latex]\sqrt {196} = \sqrt {{W^2}} [/latex]
[latex]14 = W[/latex] or [latex]W = 14\,ft[/latex]
- Step 2: Now that we know the measurement of the pool’s width or the value of the variable [latex]W[/latex], we can easily find the length.
Pool’s Length = Twice Its Width
[latex]L = 2W[/latex]
[latex]L = 2(14)[/latex]
[latex]L = 28\,ft[/latex]
- Step 3: Let’s check to verify if both dimensions will give us the pool’s area. We’ll simply multiply the length by the width, just like the area of the rectangle formula.
[latex]A = LW[/latex]
[latex]392 = 28 \cdot 14[/latex]
[latex]392\,f{t^2} = 392\,f{t^2}[/latex]
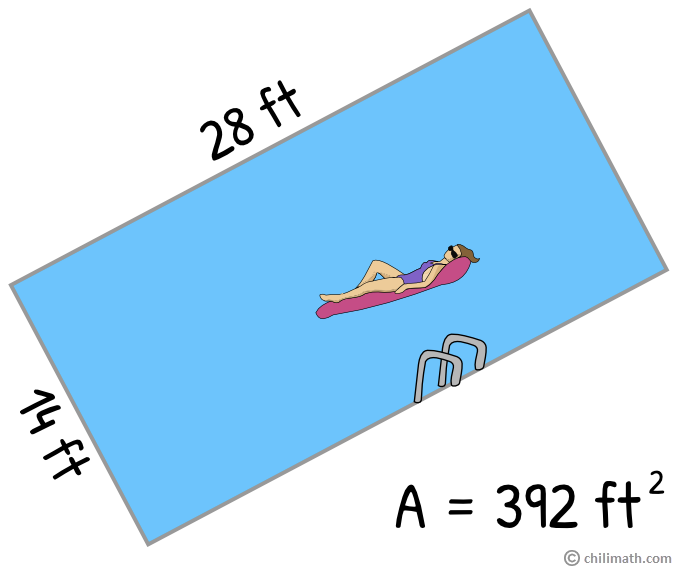
And they do! Therefore, the rectangular pool is 28 feet long and 14 feet wide.
You may also be interested in these related math lessons or tutorials:
