Perimeter of a Rectangle Word Problems

There are different types of geometry word problems. One of the most common involves the perimeter which is the distance around the outside of a two-dimensional geometric shape. In this lesson, our focus is on the perimeter of a rectangle in which we’ll find the relationship between the sides of a rectangle, that is, the length and the width.

---

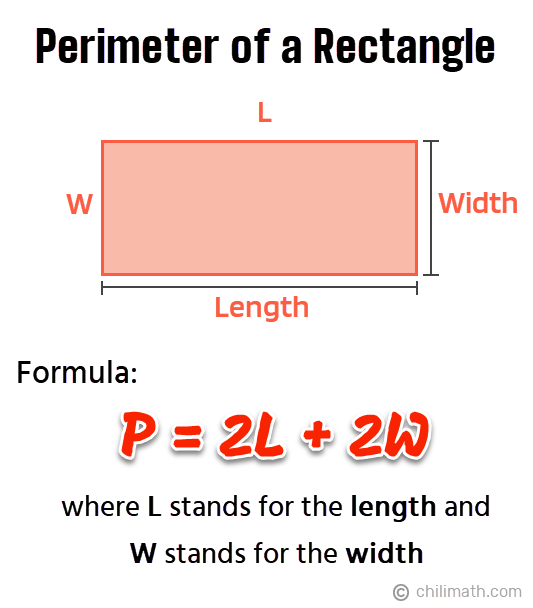
The key to solving perimeter word problems is to know two things:

1) The formula of the perimeter of a rectangle.

• Perimeter of a Rectangle Formula: [latex]{\textbf{\textit{P = 2L + 2W}}}[/latex]
• Remember that the length (L) is the longest side of the rectangle while the width (W) is the shortest side.

2) Being able to express the length in terms of the width and vice versa, depending on the word problem.

---

Let’s tackle this topic by working on a variety of examples involving the perimeter of a rectangle.

Just a heads up, the first five examples (word problems 1-5) can be solved by multi-step equations with one or single variable while the last three (word problems 6-8), can be solved by systems of equations with two variables.

Example 1: The perimeter of a rectangle is 128 centimeters and the length is 47 centimeters. Find the width of the rectangle.

The first thing that we need to do is to construct or draw a diagram based on the information given in the problem. Looking back at our problem, we were given the measurement for the length as well as the perimeter of the rectangle.

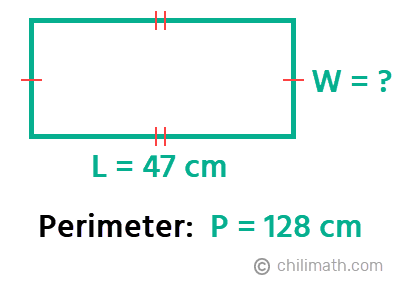
With this visual, we can easily spot what pieces of information are already provided to us and what else is missing that we need to solve. Clearly, the width is unknown so we’ll represent this value with the variable [latex]W[/latex].

Let’s now solve for the width ([latex]W[/latex]) using the formula for the perimeter of a rectangle. Since we already know the value for the length ([latex]L[/latex]) and the value for the perimeter ([latex]P[/latex]), we will simply replace the variables ([latex]L[/latex]) and ([latex]P[/latex]) with their values.

Answer: The width of the rectangle is 17 centimeters.

Before we proceed to the next problem, let’s find out if our answer is correct. We can do this by simply substituting the values that we have for the perimeter, length, and width into the perimeter formula, then verify if each side of the equation equals the other.

Check:

Great! We’re able to confirm that the measurement of the width which is 17 cm, indeed is the correct value.

---

Example 2: A rectangle has a width of 7 feet and a length of 132 inches. Find the perimeter of the rectangle both in feet and inches.

This problem is asking us to express the perimeter of the rectangle using two different units of measurement, i.e. in feet and in inches. To get both measurement units, we’ll solve the problem in two parts.

PART 1: Express the perimeter of the rectangle in feet.

We are given the following information below:

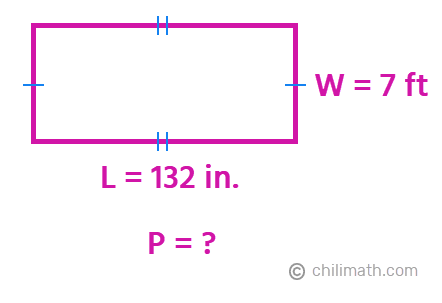
Since the width is already in feet, we don’t have to do anything with it. However, for the length, we must convert 132 inches to feet. We know that 1 ft = 12 in.

Therefore,

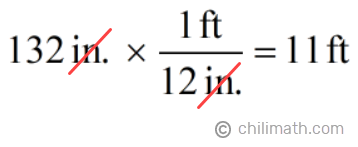
Perfect! We were able to get the measurement of our length in feet. So now, we have:

• Width = 7 ft
• Length = 11 ft

To find the perimeter, we simply have to plug in the values into the Perimeter Formula then simplify.

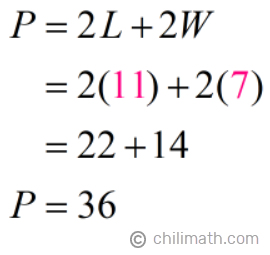
Part 1 Answer: The perimeter of the rectangle is 36 feet.

PART 2: Express the perimeter of the rectangle in inches.

We will use the same methodology in Part 1 to find our answer for this second part. Again, the following pieces of information are given to us in the original problem:

• Width = 7 ft.
• Length = 132 in.

This time, the length is the side that has its measurement already in inches. Since we want to find the rectangle’s perimeter in inches, we’ll focus on converting the width from feet to inches. Remember again that 12 in. = 1 ft.

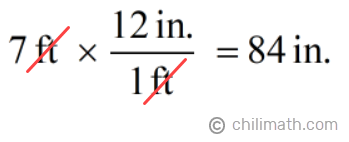
So now we have,

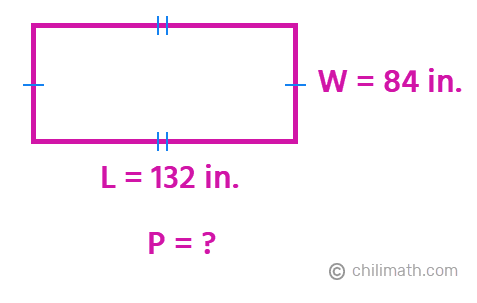
The dimensions of our length and width are now both in inches. Let’s now find the perimeter of the rectangle by substituting the values into the perimeter formula then simplify.

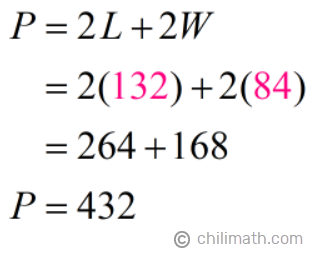
Part 2 Answer: The perimeter of the rectangle is 432 inches.

---

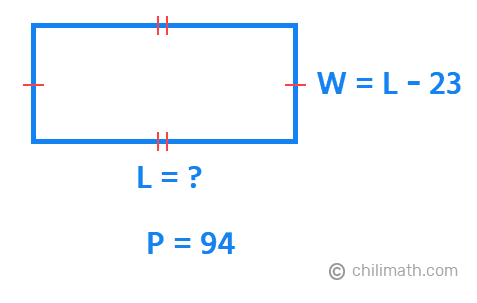
Example 3: The width of a rectangle is 23 meters less than the length. The perimeter of the rectangle is 94 meters. Find the dimensions of the rectangle.

For us to solve this word problem, we need to be able to substitute values or expressions to the [latex]L[/latex], [latex]W[/latex], and [latex]P[/latex] variables of the perimeter formula, [latex]P=2L+2W[/latex].

In our problem, we can easily spot the value of the perimeter ([latex]P[/latex]) which is 94 meters. On the other hand, the width of the rectangle is expressed in terms of length.

The width of the rectangle is 23 meters less than the length.

We need to translate the algebraic sentence above into an algebraic expression so we can substitute it for the width in the perimeter formula. So if ([latex]W[/latex]) stands for the width and ([latex]L[/latex]) is for the length, our algebraic expression for the width is,

[latex]{W = L – 23}[/latex]

How about the length? Well, at this time, our length is unknown. So in this case, we will keep the variable [latex]L[/latex] to stand for the length.

Let’s construct a diagram to get a better visual of all the information that we have so far.

Now that it’s clear to us what we’ll substitute the [latex]L[/latex], [latex]W[/latex], and [latex]P[/latex] variables with, we can proceed to solve for [latex]L[/latex] using the perimeter of a rectangle formula.

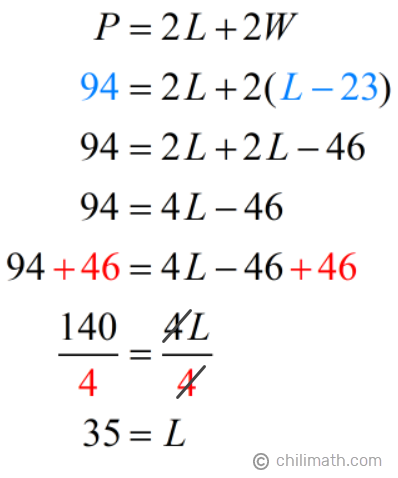
Since the problem is asking us to find the dimensions for both the length and the width, let’s use the value of [latex]L[/latex] to also get the value for the width.

• Length ([latex]L[/latex])= [latex]35[/latex]
• Width ([latex]W[/latex])= [latex]L-23={\color{red}35}-23=12[/latex]

Answer: The length of the rectangle is 35 meters and the width is 12 meters.

I advise my students to always check their answers no matter how confident they feel that they got the correct one. For this problem, we simply have to substitute the values of [latex]L[/latex], [latex]W[/latex], and [latex]P[/latex] in the perimeter formula. If the left and the right side of the equation both equal each other, then our answers are correct.

Check:

---

Example 4: The length of the rectangle is 12.5 feet more than the width. If the perimeter of the rectangle is 101 feet, how long is the length of the rectangle?

Right off the bat, we can see that the value of the perimeter is 101 ft and that the length is defined using the width as given in the following statement.

The length of the rectangle is 12.5 feet more than the width.

Just like in our previous example, we need to algebraically express the length in terms of the width so we can substitute this algebraic expression for the length ([latex]L[/latex]) in the perimeter formula. Translating the statement above, we get [latex]L = W+12.5[/latex]

Let’s put together the information that we’ve gathered so far in a diagram.

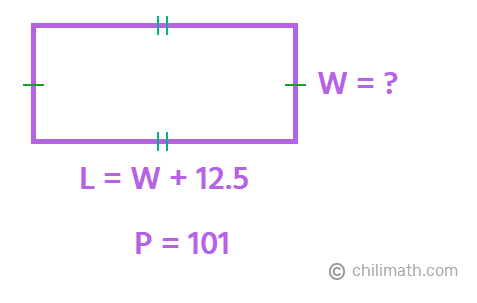
As you can see, the width ([latex]W[/latex]) is currently unknown. Therefore, the next step that we have to do is solve for ([latex]W[/latex]) using the formula for the perimeter of a rectangle.

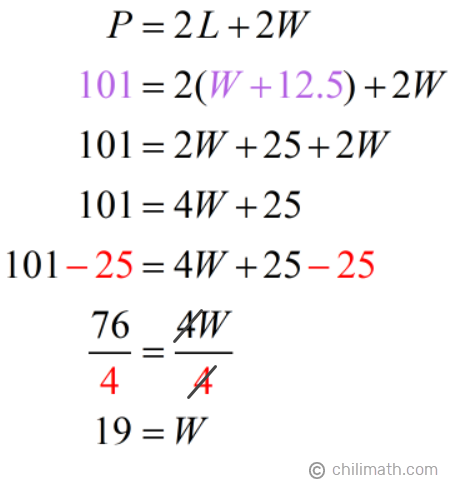
Now that we know the value of the width ([latex]W[/latex]), let’s use this value to find the dimension for the length.

• Width ([latex]W[/latex])= [latex]19[/latex]
• Length ([latex]L[/latex])= [latex]W+12.5={\color{red}19}+12.5=31.5[/latex]

Going back to our original problem, how long is the length of the rectangle?

Answer: The length of the rectangle is 31.5 ft.

This time, I will leave it up to you to check if our answer is correct. Start by substituting the values of [latex]L[/latex], [latex]W[/latex], and [latex]P[/latex] in the perimeter formula, [latex]P=2L+2W[/latex], then simplify. If both sides of the equation equal each other, then we got the correct answer.

---

Example 5: A certain rectangle has a length of half a yard more than twice the width. The perimeter of the unknown rectangle is 55 yards. Find its width.

Let’s start by determining the values and expressions that are provided to us in the problem.

• Length = half a yard more than twice the width = [latex]2W +\Large {1 \over 2}[/latex]
• Width = ?
• Perimeter = 55

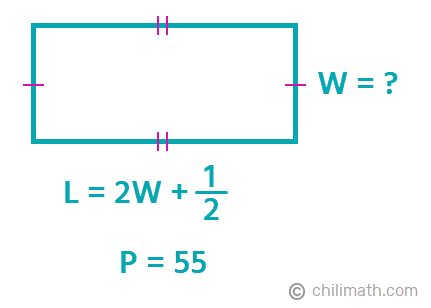
Using the perimeter formula, we will solve for the unknown which is the width ([latex]W[/latex]).

Before we formally answer the question from our word problem, let’s find out the dimensions of the rectangle using the value of the width.

• Width ([latex]W[/latex])= [latex]9[/latex]
• Length ([latex]L[/latex])= [latex]2W +{\Large {1 \over 2}}=2({\color{red}9})+{\Large {1 \over 2}}=18+{\Large {1 \over 2}}=18{\Large{1 \over 2}}[/latex]

Answer: The width of the rectangle is 9 yards.

---

Example 6: When you subtract the width from the length of the rectangle, the difference is 8 inches. What are the dimensions of the rectangle if its perimeter is 72 inches?

This example is a little bit more complex than the previous ones. As you may have noticed, neither the length nor the width is expressed in terms of the other. So to proceed, we will start by discussing the important statements that are given to us in this problem.

When you subtract the width from the length of the rectangle, the difference is 8 inches.

Let’s use again the variable [latex]L[/latex] to stand for length and [latex]W[/latex] for the width. Translating this algebraically, we have the following equation

[latex]L – W = 8[/latex]

The perimeter of the rectangle is 72 inches.

We are already familiar with the formula for the perimeter of a rectangle so we can simply write this as

[latex]P = 2L + 2W[/latex]

[latex]72 = 2L + 2W[/latex]

By just going through both statements, we were able to come up with two equations:

• Equation 1: [latex]L – W = 8[/latex]
• Equation 2: [latex]72 = 2L + 2W[/latex]

It is clear at this point that we are dealing with two equations with two unknowns, namely, [latex]L[/latex] and [latex]W[/latex]. In other words, we are going to solve systems of linear equations with two variables.

Observe that we can use Equation 1 to express the length in terms of the width, then substitute the expression into Equation 2. The result will be a multi-step equation having the width ([latex]W[/latex]) as the only variable in the equation.

Let’s do this step-by-step.

1) Start with Equation 1 and solve for [latex]L[/latex].

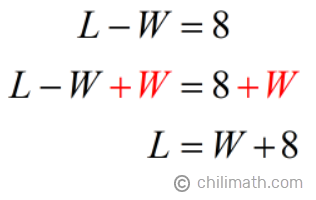
Notice that to clean up the left side of the equation, we added [latex]W[/latex] to both sides of the equation. Then we applied the Commutative Property of Addition, that is, [latex]8 + W = W + 8[/latex].

2) Next, substitute the expression of [latex]L[/latex] into Equation 2.

We now have the value for the width. But since we are asked to find both dimensions of the rectangle, let’s plug the value of the width which is 14 into Equation 1 to find the value for the length ([latex]L[/latex]).

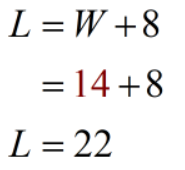
So, what are the dimensions of the rectangle if its perimeter is 72 inches?

Answer: The length of the rectangle is 22 inches while the width is 14 inches.

Calculator Check:

---

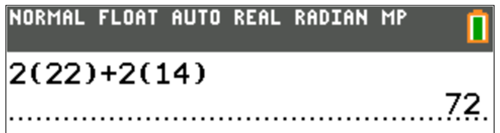
Example 7: The difference of the length and three times the width of a rectangle is 5 centimeters. Find the length and the width of the rectangle if its perimeter is 82 centimeters.

We have the same situation here as our previous example. Neither the length nor the width is expressed in terms of the other. Therefore, let’s break down the problem again to find out what important pieces of information are given to us.

First, we are told that

The difference between the length and three times the width of a rectangle is 5 centimeters.

Using [latex]L[/latex] and [latex]W[/latex] again as our unknown variables, we can translate this algebraic sentence as

[latex]L – 3W = 5[/latex]

Next, our second statement says that

The perimeter of the rectangle is 82 centimeters.

This one is easy. Using the formula for the perimeter of a rectangle we have,

[latex]P = 2L + 2W\,\,\, \to \,\,\,82 = 2L + 2W[/latex]

Before we proceed, let’s look at our two equations:

• Equation 1: [latex]L – 3W = 5[/latex]
• Equation 2: [latex]82 = 2L + 2W[/latex]

Our next step is to express [latex]L[/latex] in terms of the width.

1) Solve for [latex]L[/latex] using Equation 1.

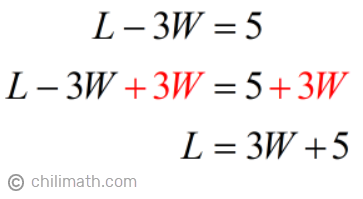
We are now ready to plug in the expression of [latex]L[/latex] into our second equation.

2) Substitute [latex]L[/latex] with [latex]3W + 5[/latex] in Equation 2.

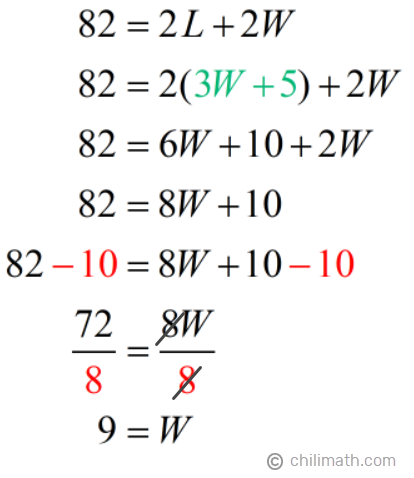
Let’s now also see what the value of the length is using the value we got for the width which is 9.

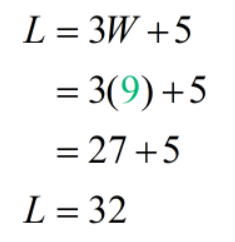
Answer: The length of the rectangle is 32 centimeters and the width is 9 centimeters.

Calculator Check:

Let’s verify again real quick using a calculator if both values will give us a perimeter of 82 cm when plugged into the formula of the perimeter of a rectangle. If the sum of twice the length ([latex]2L[/latex]) and twice the width ([latex]2W[/latex]) is 82, then both of our answers are correct.

---

Example 8: The sum of the length and one-half of the width is 42 yards. The rectangle’s perimeter is 100 yards. What is the width of the rectangle?

You should be familiar by now with what to do first when we have perimeter word problems where neither each side of the rectangle is defined using the other.

Let’s delve into the important statements right away and translate them into an algebraic equation.

The sum of the length and one-half of the width is 42 yards.

• Equation 1: [latex]L + {\Large{1 \over 2}}W = 42[/latex]

The rectangle’s perimeter is 100 yards.

• Equation 2: [latex]P = 2L + 2W\,\,\, \to \,\,\,100 = 2L + 2W[/latex]

What’s next? Well, it’s time for us to define the length using the width by solving for [latex]L[/latex] using Equation 1.

Let’s now substitute [latex]L[/latex] with [latex]42 – {\Large{1 \over 2}}W[/latex] in Equation 2.

The word problem is only asking us for the measurement of the width. So we’ll say,

Answer: The width of the rectangle is 16 yards.

I’ll leave it up to you to do the checking if our answer is correct. Make sure to find the value of the length first by using the value of the width ([latex]W[/latex]) which is 16.

Then, move on to check if both values, when plugged into the perimeter of a rectangle formula ([latex]P=2L+2W[/latex]), will give you a perimeter of 100 yards as stated in our original word problem.

---

You may also be interested in these related math lessons or tutorials:

Perimeter of a Rectangle

Area of a Rectangle