Perimeter of a Rectangle Formula

The perimeter of a rectangle is the distance around the rectangle. Consider the perimeter of a rectangular flower garden to be the length of the fence that surrounds the garden. We calculate the perimeter of a rectangle by getting the sum of all its sides.

---

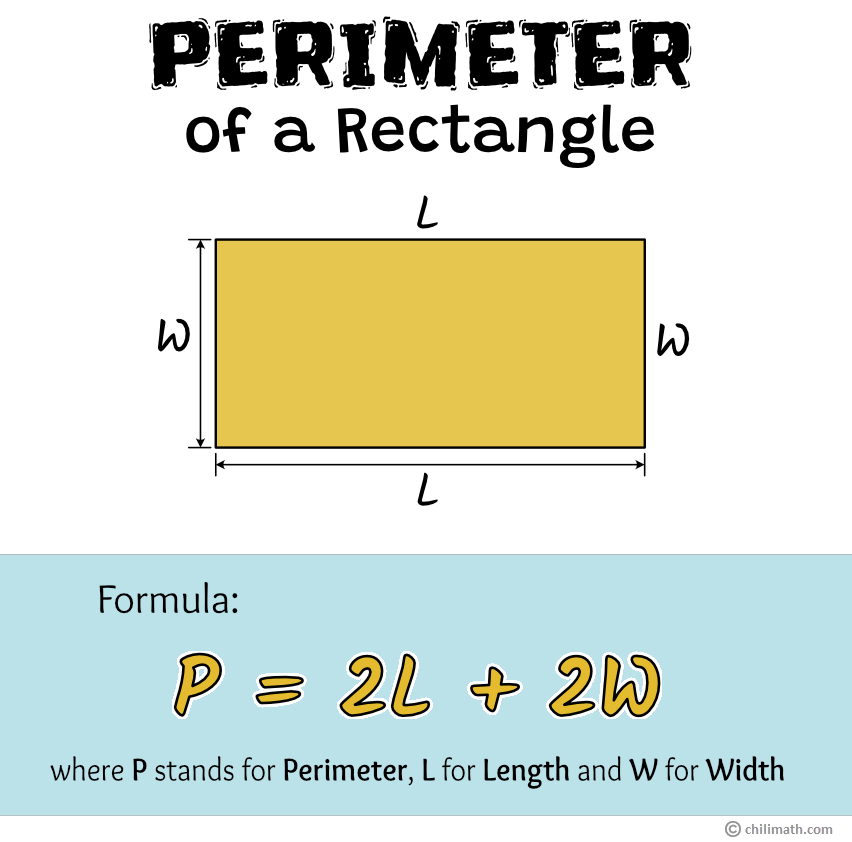
How to Find the Perimeter of a Rectangle

As we all know, a rectangle has four sides and four right angles. However, when compared to a square, not all of its side measurements are equal. Two pairs of opposite sides in a rectangle have equal measurements. That is, the length on one side is congruent with the length on the other side, and the width on one side is congruent with the width on the other side.

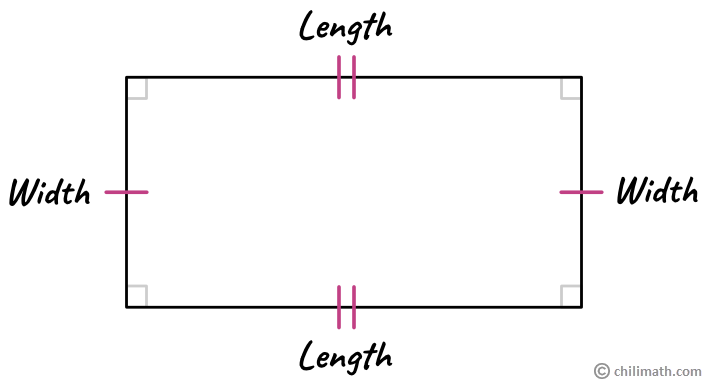
Note: The number of tick marks indicates congruent sides. Also remember that the length ([latex]l[/latex]) is the longest side while the width ([latex]w[/latex]) is the shortest side.

We find the perimeter of a rectangle by adding all the measurements of its sides. If we write this in an equation, it looks like this:

[latex]P = l + w + l + w[/latex]

where [latex]P[/latex] stands for perimeter, [latex]l[/latex] for length, and [latex]w[/latex] for width

However, since the opposite sides of a rectangle are congruent, the equation can be simply written as [latex]P = 2l + 2w[/latex].

As you may have noticed, the length and the width are multiplied by two in the formula then added together rather than writing the length and the width twice.

---

Finding the Perimeter of a Rectangle Examples

There is no better way to practice using this formula and learning more about the perimeter of a rectangle than to go over some examples. Alright, let’s begin!

Example 1: Find the perimeter of the rectangle.

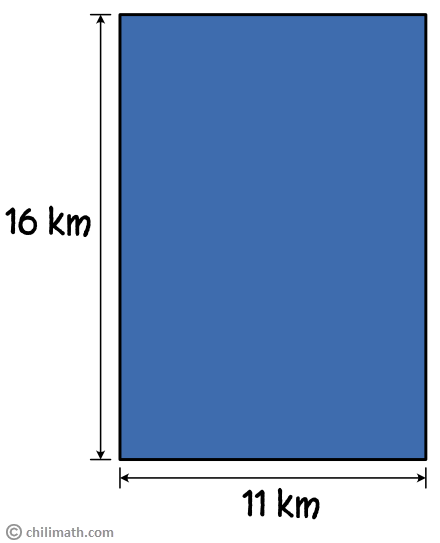
The rectangle above has a length of 16 km and a width of 11 km. Even though we are not given the measurements of all four sides, we know that the other two sides also measure 16 km and 11 km, respectively. How? Because the opposite sides of a rectangle are congruent. In other words, we only need to know the length and the width to be able to calculate a rectangle’s perimeter.

Now let’s use the formula for a rectangle’s perimeter and plug in [latex]16[/latex] for [latex]L[/latex] and [latex]11[/latex] for [latex]W[/latex].

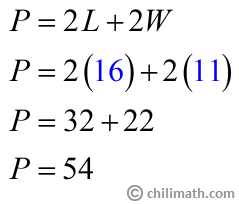
The perimeter of the rectangle is 54 km.

---

Example 2: How long is the rectangle below if its perimeter is 154 ft and its width measures 25 ft?

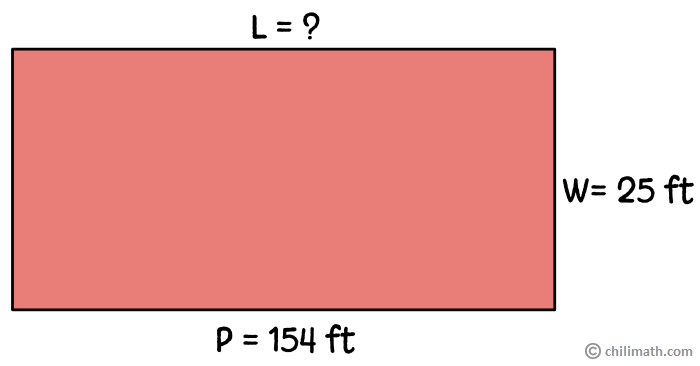
Sometimes, you’ll be presented with a problem wherein one of the dimensions is missing. In this problem, we are asked to find the rectangle’s length rather than calculating its perimeter. Finding the missing length or width is easy as long as you have both the measurement of one of the dimensions and the rectangle’s perimeter.

To find the missing length, all we have to do is use the perimeter of a rectangle formula, substitute [latex]P[/latex] with [latex]154[/latex] and [latex]W[/latex] with [latex]25[/latex], then solve for [latex]L[/latex].

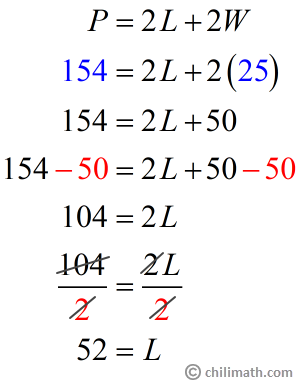
Perfect! The length of the rectangle is 52 ft. However, before we wrap up this problem, let’s verify to make sure that the our length and width will indeed give us a perimeter of 154 ft. Using the formula again, we have

[latex]P = 2L + 2W[/latex]

[latex]154 = 2\left( {52} \right) + 2\left( {25} \right)[/latex]

[latex]154 = 104 + 50[/latex]

[latex]154 = 154[/latex]

And yes, it does! Therefore, the length of the rectangle is 52 feet.

---

Example 3: If the length and width of the rectangle below are both decreased by 4 inches, find the perimeter of the new rectangle.

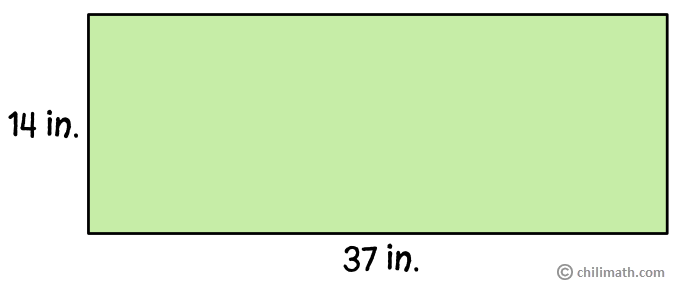
In this example, we are asked to decrease the measurements of our original rectangle by 4 inches then using these new dimensions, we will find the perimeter of the new rectangle.

Step 1: Decrease the original (current) rectangle’s length and width by 4 inches.

• Length:

[latex]L = 37 \color{red}{- 4}[/latex]

[latex]L = 33[/latex]

• Width:

[latex]W = 14 \color{red}{- 4}[/latex]

[latex]W = 10[/latex]

We got the dimensions for the new rectangle. The length is now 33 inches and the new width is 10 inches.

Step 2: Calculate the new rectangle’s perimeter using the new length and width.

• Substitute [latex]33[/latex] for [latex]L[/latex] and [latex]10[/latex] for [latex]W[/latex] into the perimeter of a rectangle formula.

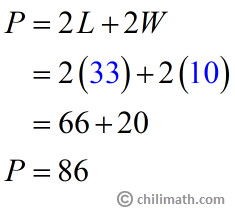
Here it is! The perimeter for our new rectangle is 86 inches.

---

Example 4: The length of a rectangle is twice its width. What is the perimeter of the rectangle with a width of 6.8 centimeters?

Before going into any calculations, let’s first identify and interpret the pieces of information given to us in the problem.

• Width ([latex]W[/latex]): [latex]6.8\,cm[/latex]

• Length ([latex]L[/latex]): Twice the width → [latex]6.8\left( 2 \right) = {13.6\,cm}[/latex]

Now that we have our length and width, we can proceed as normal to find the perimeter of the rectangle.

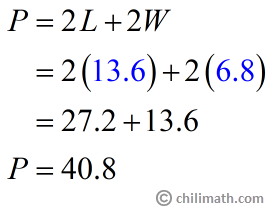
The rectangle’s perimeter is 40.8 centimeters.

---

Example 5: Our neighbor has a rectangular pool that is 36 feet long. If the pool’s perimeter is 108 feet, how wide is the pool?

One of the measurements is missing in this problem just like in one of our previous examples. In this case, the measurement of the pool’s width is unknown. To have a better picture of the problem, let’s first draw it out using the pieces of information given to us.

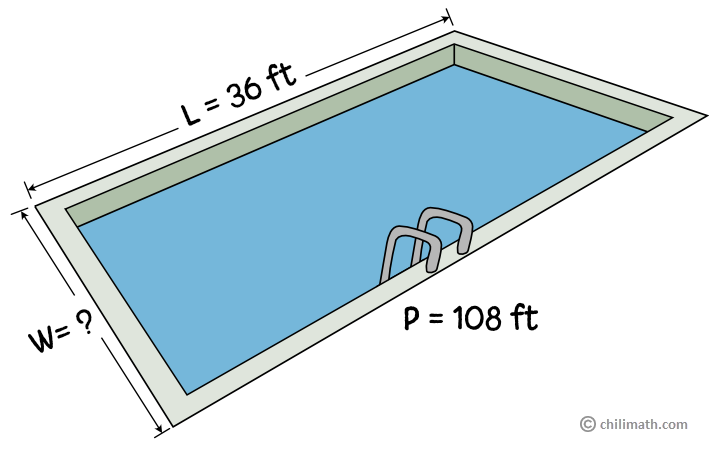
Let’s now find the width using the formula for the rectangle’s perimeter.

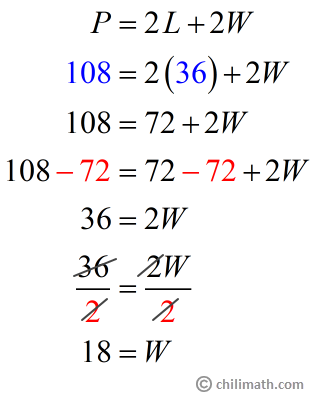
I’ll leave it up to you to verify if our length and width will indeed give us a perimeter of 108 feet.

Our neighbor’s pool is 18 feet wide.

---

Example 6: Samantha wants to put a border around a picture of her and her cat. The picture is 14 inches by 18 inches. How much border does Samantha need?

Let’s start again by identifying the pieces of information available to us.

Since she wants to put a border around the rectangular picture, we immediately know that we are dealing with a problem that involves the perimeter of a rectangle. To find how much border she needs, we need to simply apply the formula to find the perimeter of a rectangle.

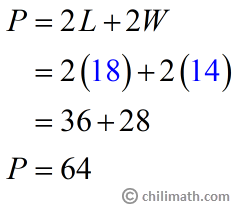
Purrfect! Samantha needs 64 inches of border to put around the picture of her and her cat.

---

You might also be interested in:

You may also be interested in these related math lessons or tutorials:

Perimeter of a Rectangle Word Problems

Area of a Rectangle

Perimeter of a Square