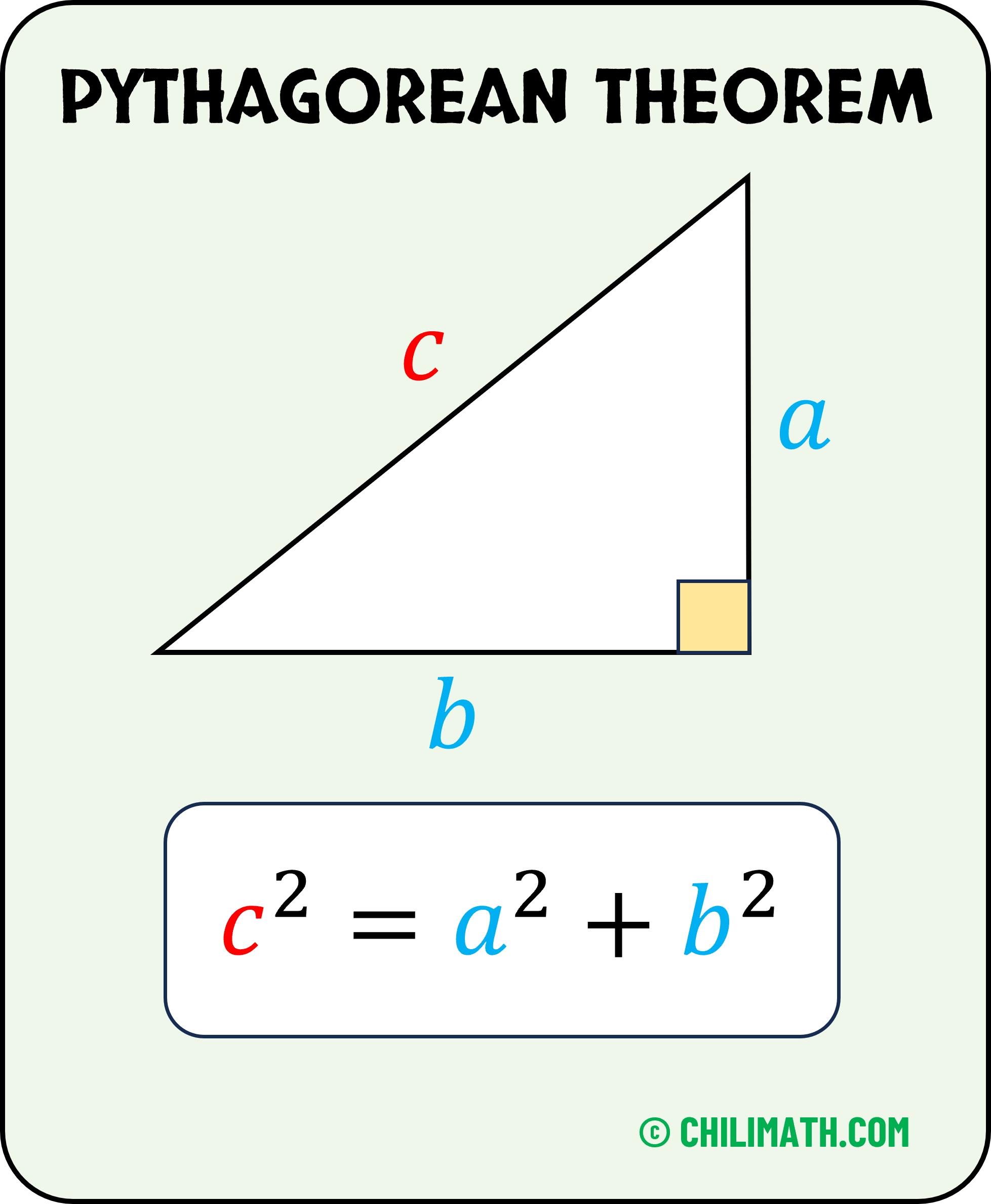
Deriving the Pythagorean Theorem Formula

From our previous lesson, we discussed the Pythagorean Theorem Formula. It states that the square of the longest side of a right triangle is equal to the sum of the squares of the shorter sides. That is, [latex] {c^2}={a^2} + {b^2}[/latex], where [latex]c[/latex] is the longest side and [latex]a[/latex] and [latex]b[/latex] are the short sides of the right triangle.

Pythagorean Theorem which is algebraically expressed as a^2+b^2=c^2

In this tutorial, our goal is to provide an algebraic demonstration of why the Pythagorean Theorem Formula holds true. The proof is straightforward and relies on a simple geometric setup. From this setup, we will construct an equation that we’ll simplify to reach the desired conclusion.

  • Let’s begin by drawing a square.
a gray square
  • Create a smaller square inside the larger square that we’ve previously drawn, ensuring to slightly tilt or rotate this new square.
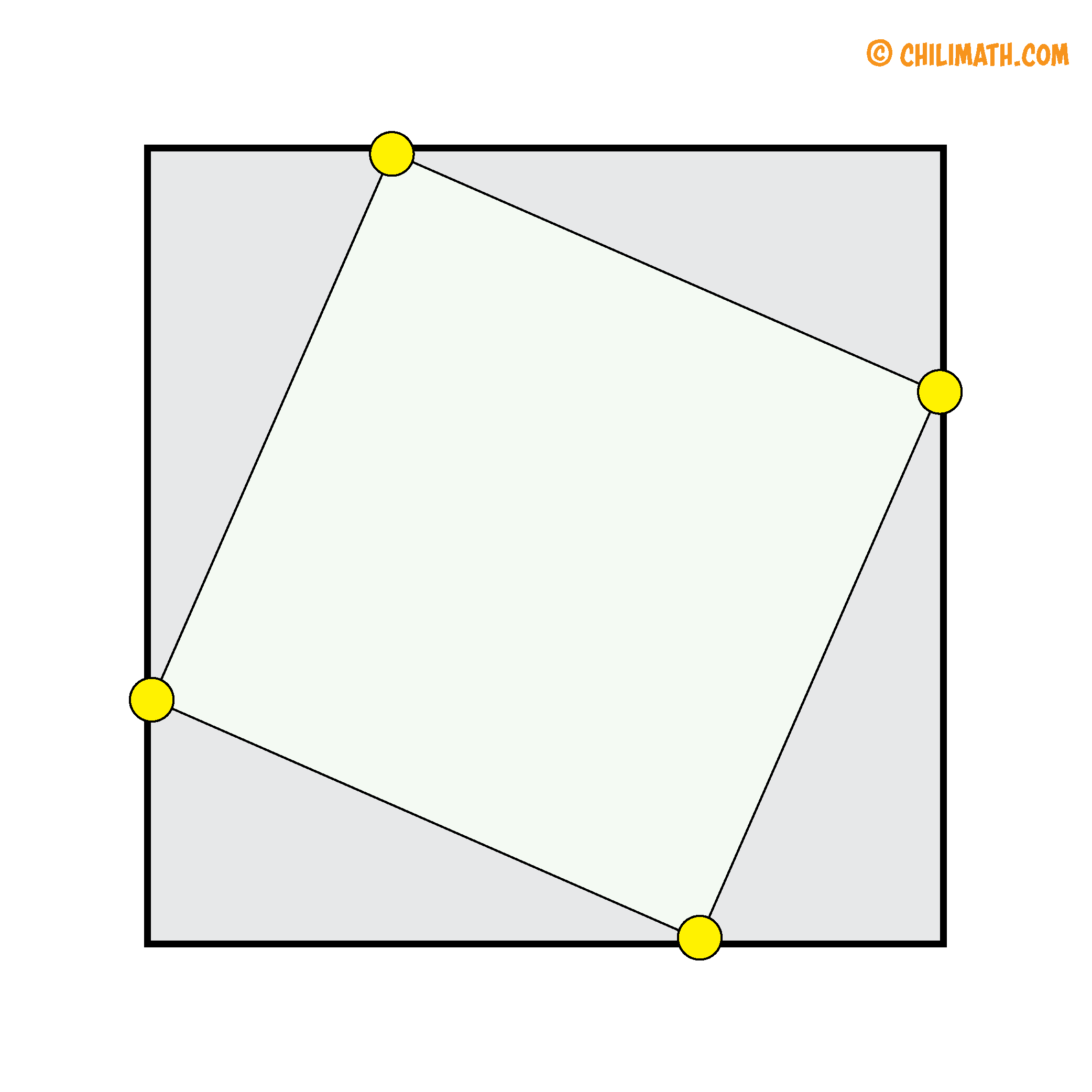
a square showing an inner square that is titled where its vertices are tangent or touching to the sides of the outer square
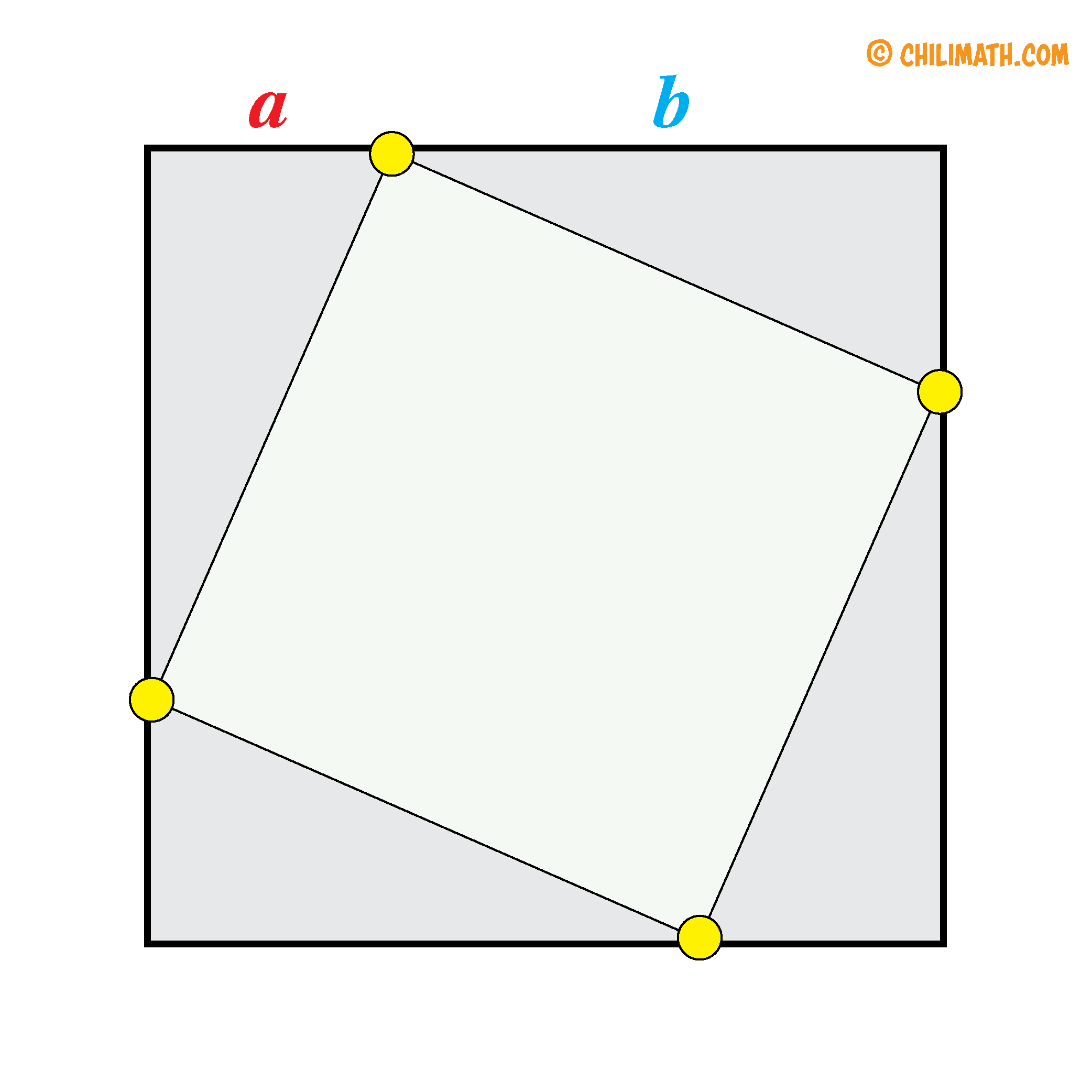
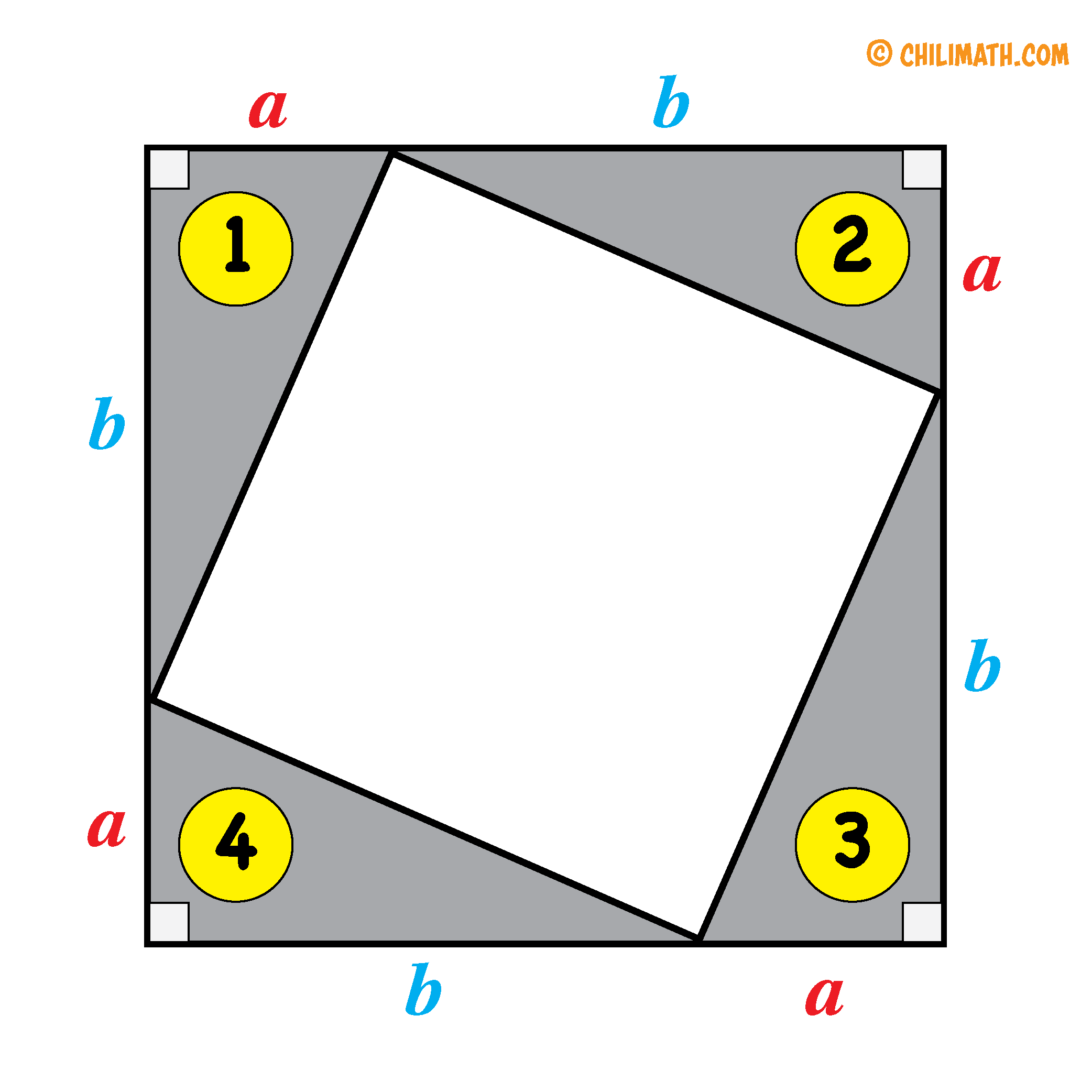
  • Notice how each corner or vertex (highlighted in yellow for emphasis) of the inner square divides the side of the larger or outer square into two line segments of different lengths. Let’s label the shorter line segment as [latex]\large\color{red}a[/latex] and the longer segment as [latex]\large\color{blue}b[/latex].
the length of the side of a square is the sum of line segment a and line segment b
  • Now, we label the remaining sides of the larger square. Remember, the shorter line segment is marked as [latex]\large\color{red}a[/latex] while the longer line segment is [latex]\large\color{blue}b[/latex].
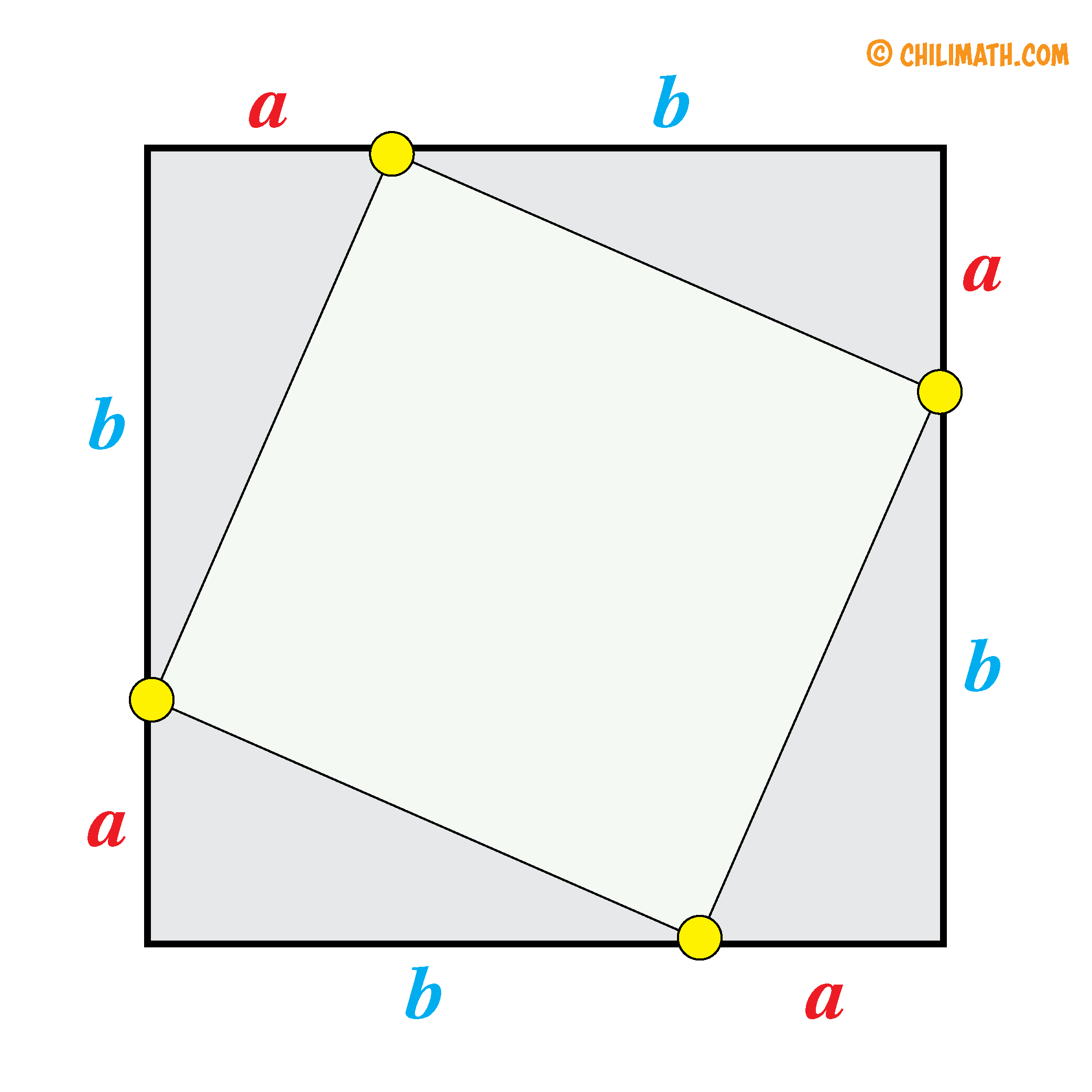
large square with all sides marked with side measure of (a+b)

Finally, we label each side of the inner square as [latex]\large\textbf{\color{green}c}[/latex].

FIGURE 1

a large square with an inner square square and inner four congruent triangles

Using the diagram above (Figure 1), we can express the area of the main or large square in two ways by constructing an equation.

Area of large square = Area of four triangles + Area of small square

Area of Large Square

If we focus our attention on the large square, its side can be found by adding the line segments [latex]\large\color{red}a[/latex] and [latex]\large\color{blue}b[/latex], that is, [latex]{\large\color{red}a}+{\large\color{blue}b}[/latex]. Since the area of a square is equal to the square of its side, we have [latex]({\large\color{red}a}+{\large\color{blue}b})^2[/latex].

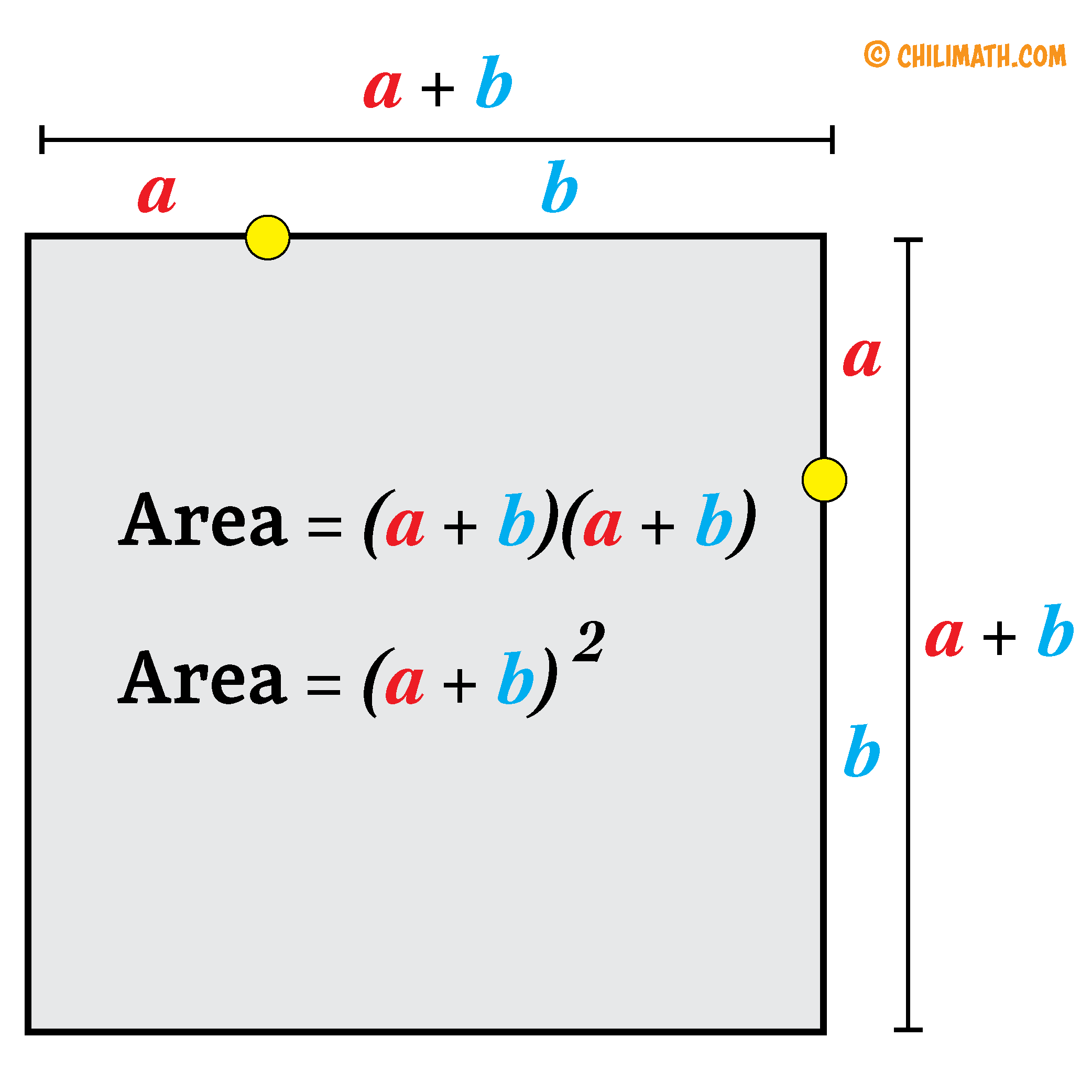
the area of the large square is (a+b) times (a+b)

Now, we will consider figuring out another way of calculating the area of the large square. Notice that in Figure 1 above, there are four (4) congruent right triangles inside the large square, and smaller square with side [latex]c[/latex].

Therefore, another way to find the area of the large square is to sum up the area of the four (4) right triangles and the area of inner square.

Let’s start by finding the area of the four triangles.

Area of the Four (4) Triangles

Remember, in order to find the area of a triangle we need to multiply the base with its height then divide the product by [latex]2[/latex].

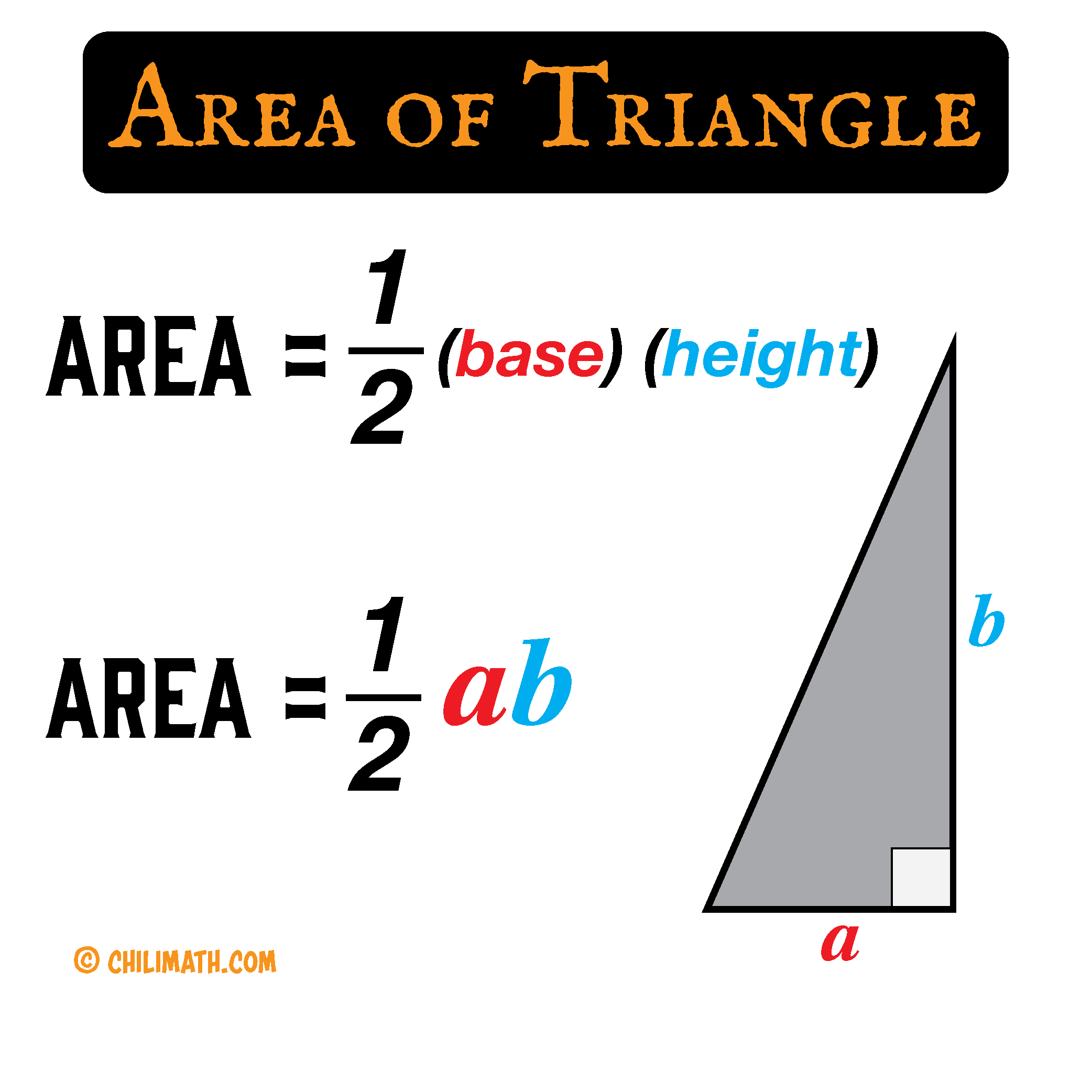
the area of a triangle equals 1/2 times a times b

However, if we again examine Figure 1 above, clearly there are four (4) congruent triangles inside the large square.

there are four congruent triangles in the inner square

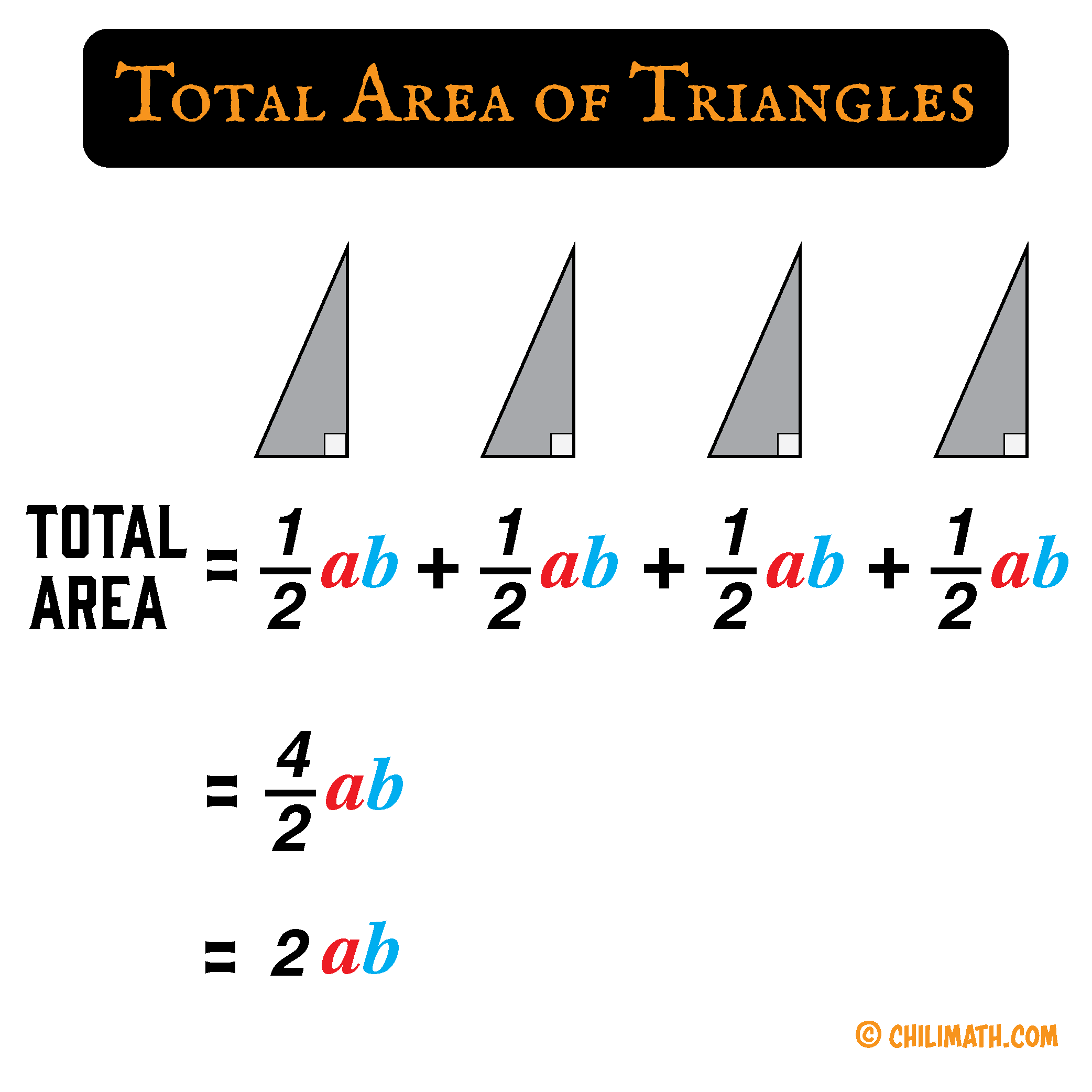
As we’re already familiar with how to find the area of a triangle, our next step is to add together the areas of four (4) triangles. The calculation below will show us that we should get [latex]2ab[/latex].

total area of four triangles equals 2ab

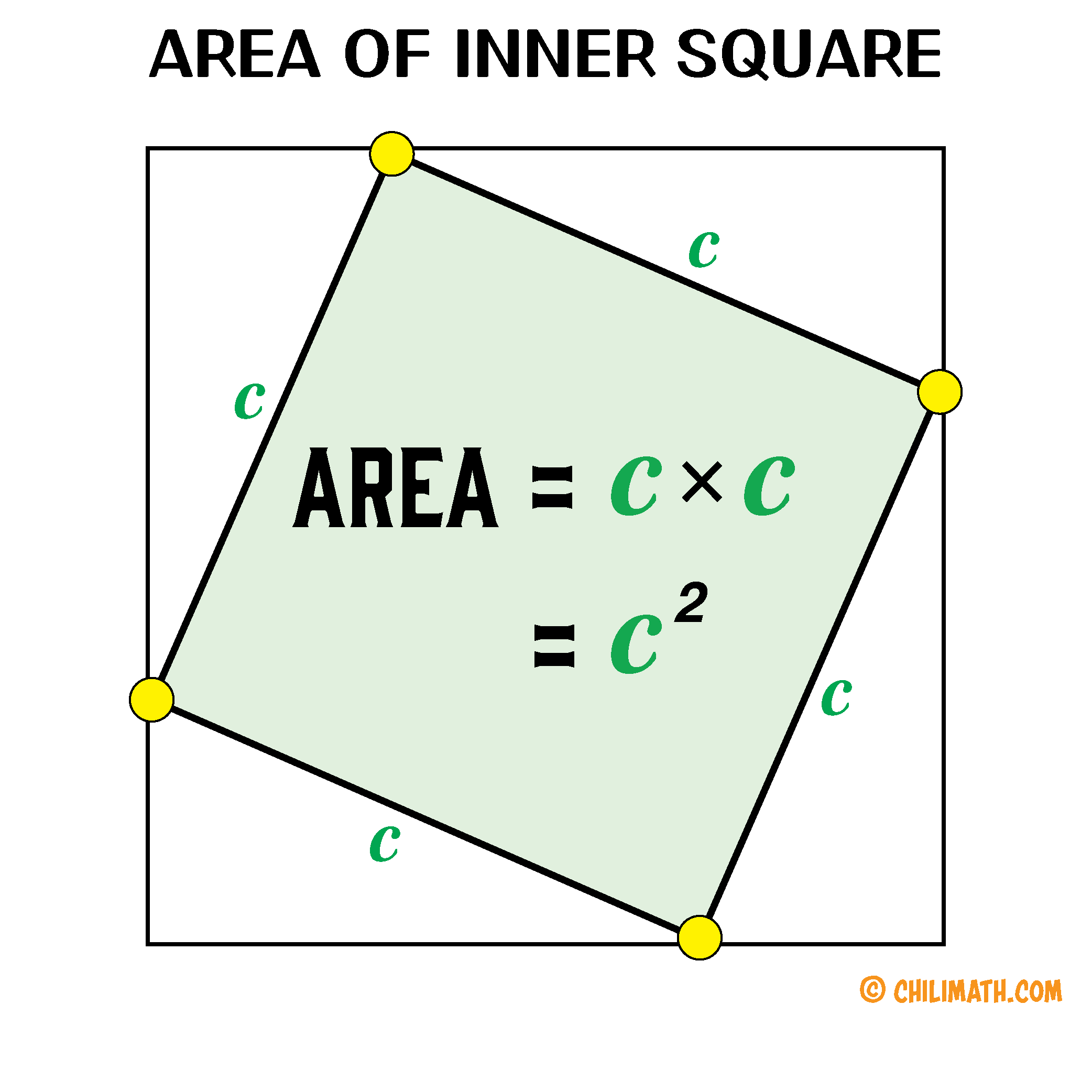
Area of the Inner Square

The subsequent step involves finding the area of the square inside the larger square. We should be familiar with the process of calculating the area of a square , which is achieved by multiplying its side length by itself. Therefore, if we represent the side length of the square as “[latex]s[/latex]”, its area can be expressed as “[latex]s^2[/latex]”. In this particular case, the side length of the inner square is denoted by the letter “[latex]c[/latex]” indicating that its area is simply “[latex]c^2[/latex]”.

area of the inner square equals c^2

Putting it All Together

Now that we have all the essential ingredients, it’s time to incorporate the missing information into the equation that we’ve established above. Allow me to rewrite it below as a reminder.

Area of large square = Area of four triangles + Area of small square

For the left side of the equation, we will substitute the area of the large square which is [latex]{\left( {a + b} \right)^2}[/latex]. This can be further expanded as [latex]{a^2} + 2ab + {b^2}[/latex].

For the right side of the equation, the total area of the four triangles can be expressed as the sum of the individual areas of the triangle. That means,

\begin{align*} {1 \over 2}ab + {1 \over 2}ab + {1 \over 2}ab + {1 \over 2}ab &= {4 \over 2}ab \\ \\ & = \boxed{2ab} \end{align*}

In addition to the right side of the equation, the area of the inner square is expressed as [latex]c^2[/latex].

Putting them together in the same equation and simplifying, we have:

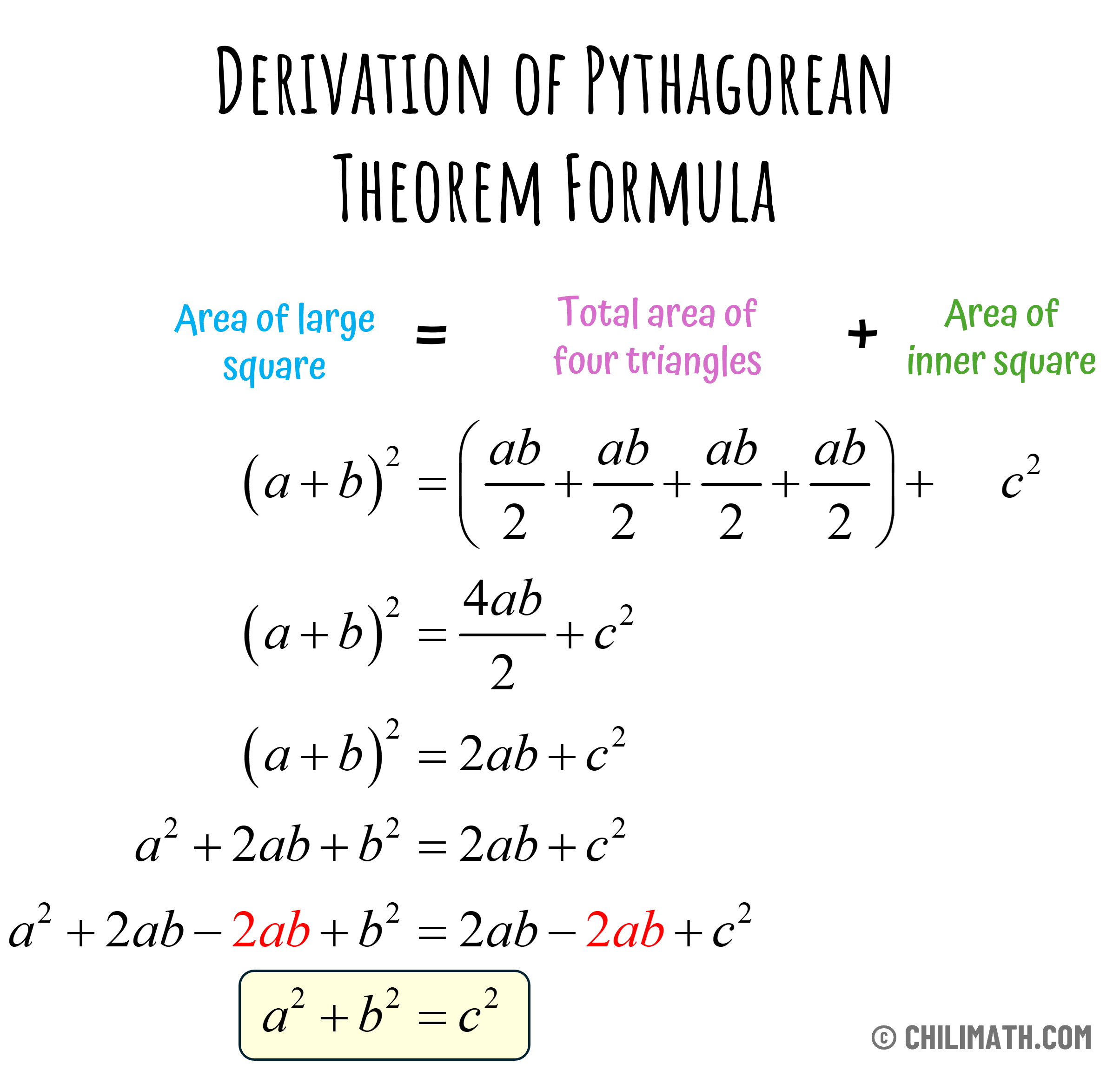
a^2+b^2=c^2

Therefore, we arrived at the Pythagorean Theorem Formula [latex]\color{red}a^2+b^2=c^2[/latex], as desired.