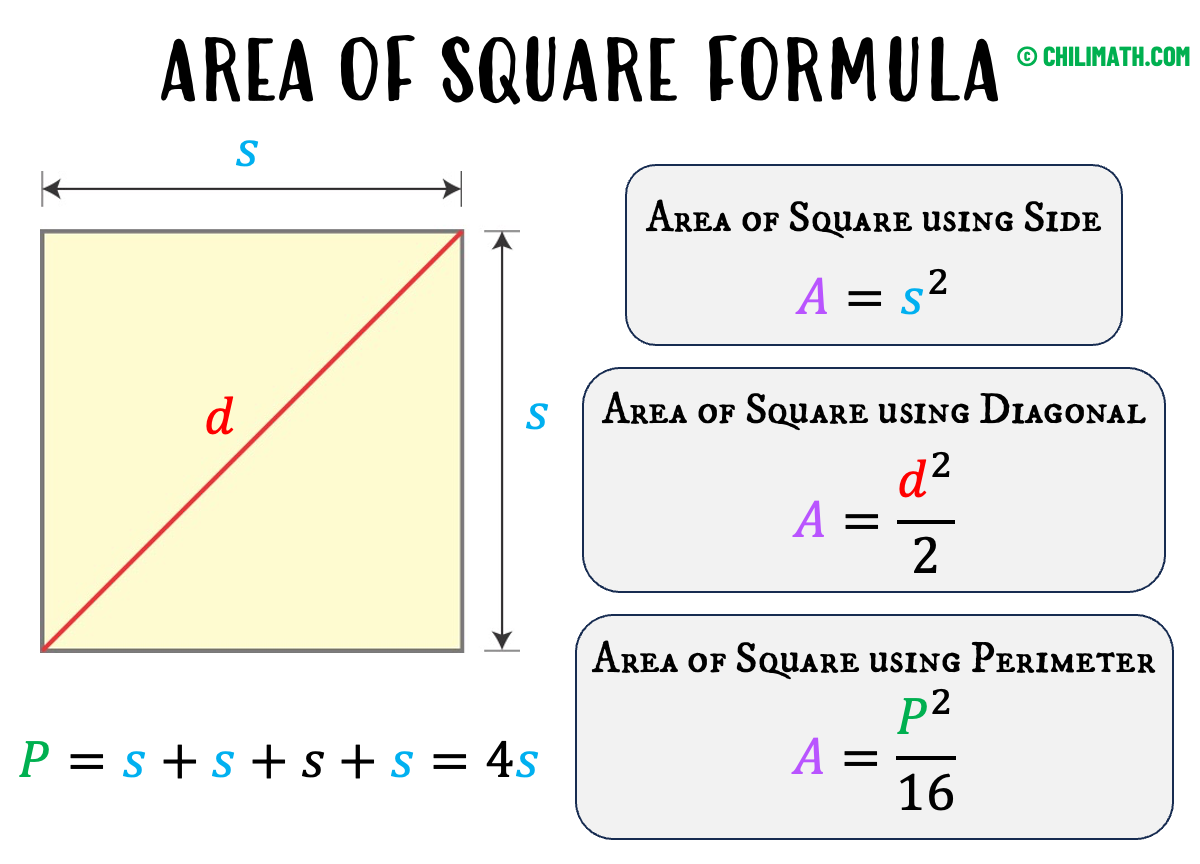
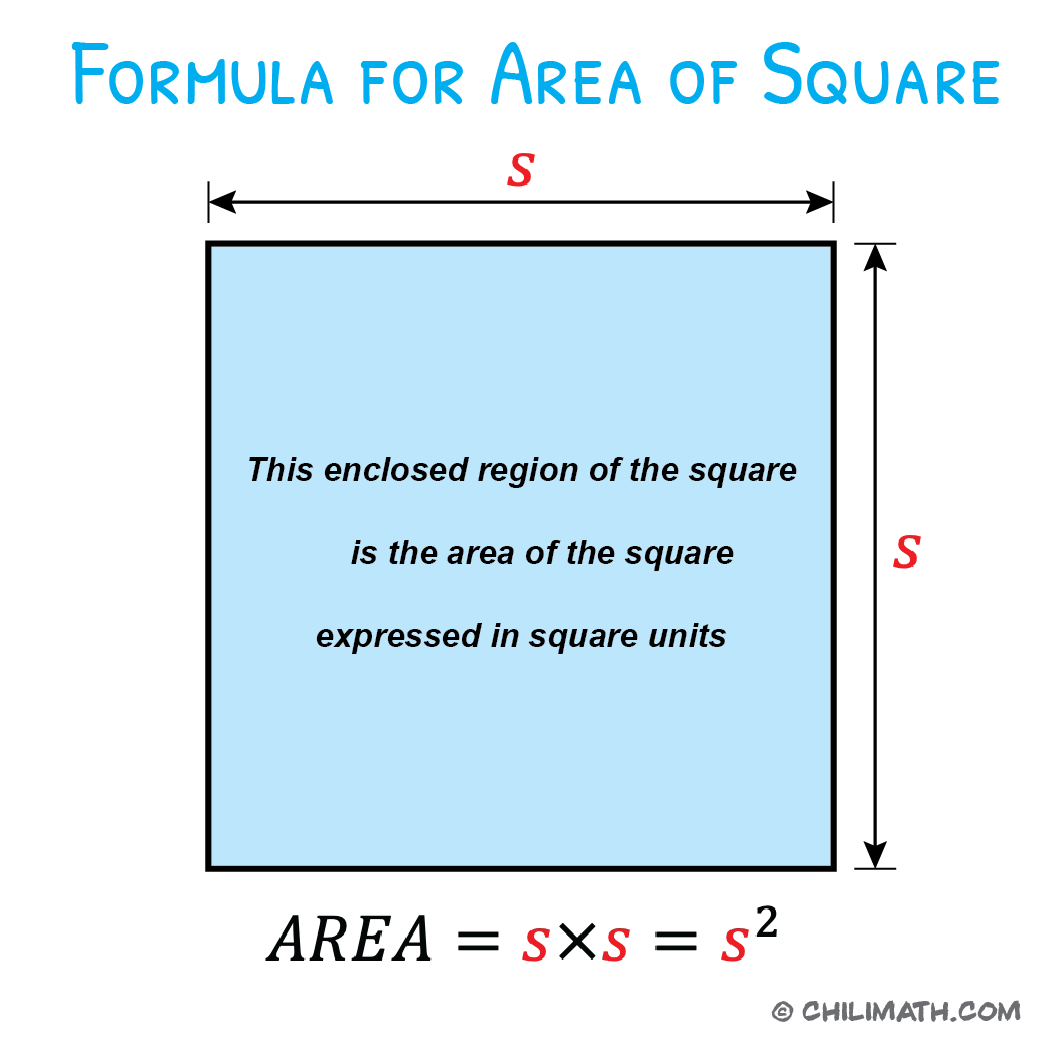
Area of Square Formula
The area of a square is the space or region enclosed by the square’s boundary. As you can see in the following illustration, the colored region within the boundary is the area of the square. For emphasis, the borders are colored green, while the area is colored orange/yellow.
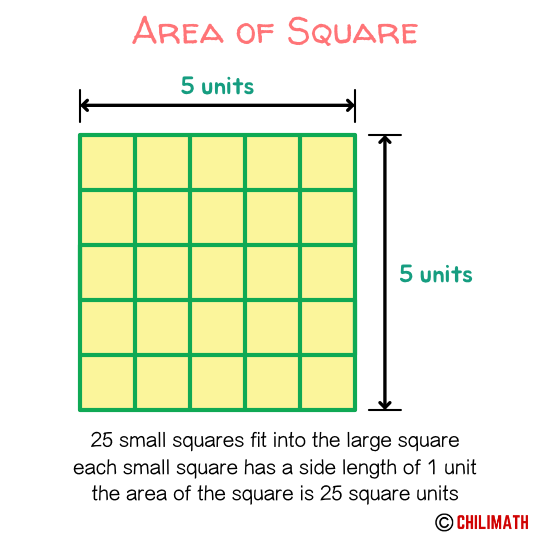
Intuitively, the area of a square can be calculated by counting the number of unit squares that are needed to entirely fill or cover the space of the square.
In the diagram below, a large square with a side length of [latex]5[/latex] units can fit [latex]25[/latex] small squares such that each smaller square has a side length of [latex]1[/latex] unit. Loosely speaking, the number of little congruent squares that cover the space within the big square is square’s area. As a result, the area is [latex]25[/latex] square units.
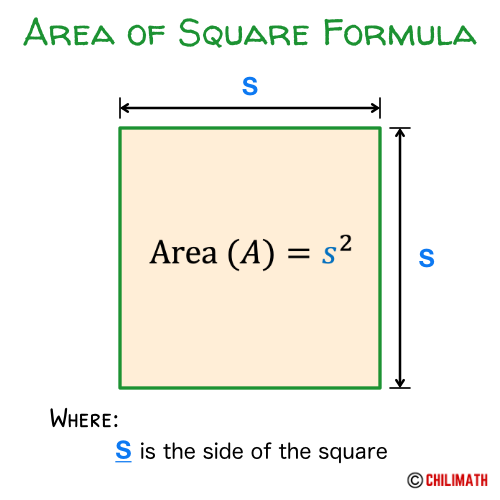
Finding Area of Square Using its Side
How do we find the area of a square using a formula? First, let’s recognize that a square is a special type of rectangle.
Remember, the area of rectangle is the product of its length and width.
[latex]A = lw[/latex]
But in the case of square, the length is equal to the width.
[latex]l = w[/latex]
So, we can express the formula of the area either in terms of the length [latex]l[/latex] or width [latex]w[/latex].
[latex]A = \left( l \right)\left( l \right) = {l^2}[/latex] [latex]\\[/latex]
[latex]A = \left( w \right)\left( w \right) = {w^2}[/latex]
Yet, when discussing squares, the terms “length” and “width” are interchangeable and can lead to misunderstandings because they refer to the same thing. It is preferable to refer to the length or width as simply the side [latex]s[/latex] in order to avoid any confusion.
We can simplify the formula by replacing [latex]l[/latex] for length or [latex]w[/latex] for width by [latex]s[/latex] to mean side.
[latex]l \to s[/latex] [latex]\\[/latex]
[latex]w \to s[/latex]
Therefore, the formula of the area of square becomes
[latex]A = \left( s \right)\left( s \right) = {s^2}[/latex]
Let’s go over some examples!
Examples of Finding Area of Square on a Grid
Example 1: Find the area of the square below on a grid.
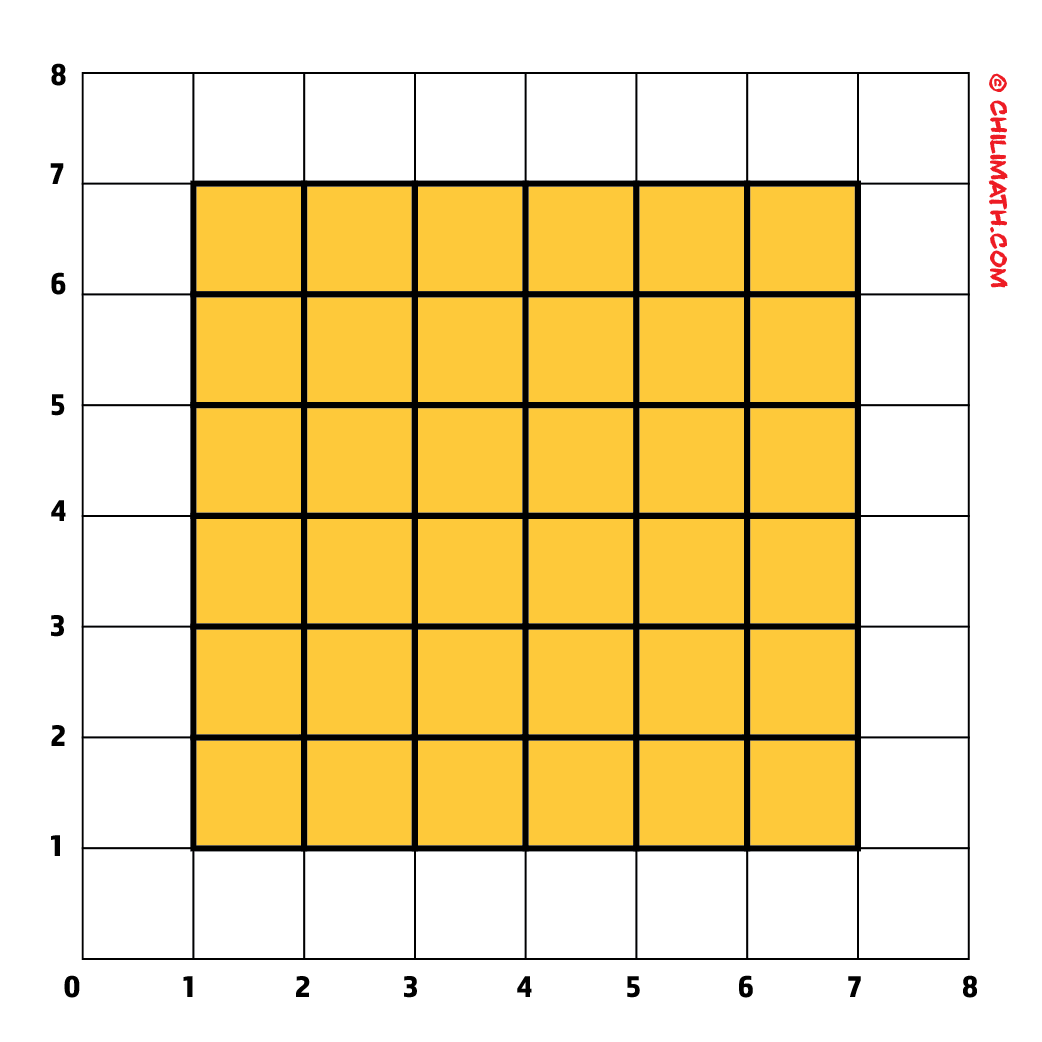
To find the area of a square on a grid paper, simply count the number of smaller squares contained within the larger square whose area you wanted to determine.
Let’s begin at 1 and keep going until we’ve counted all the squares. We will record the numbers in the squares to keep track of the total number of squares.
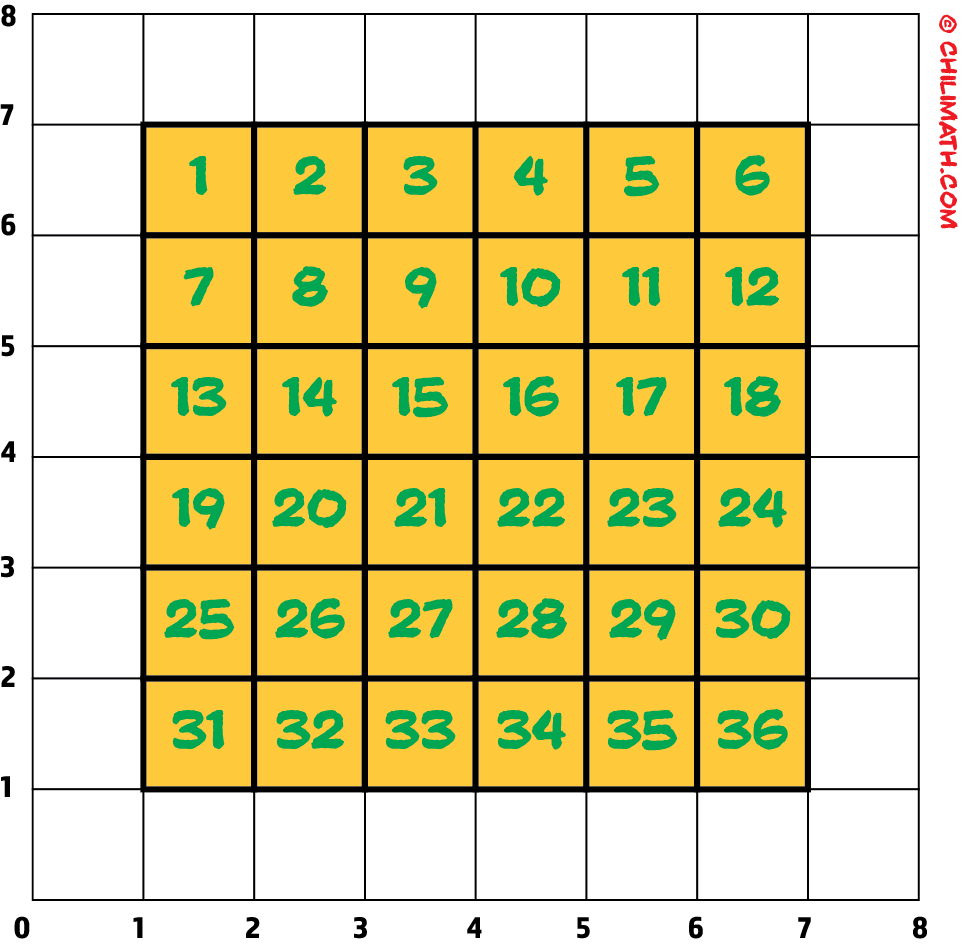
Since there are 36 small squares that cover the big square, it implies that the area of the square is 36 square units.
Example 2: What is the total area of the two squares on the grid?
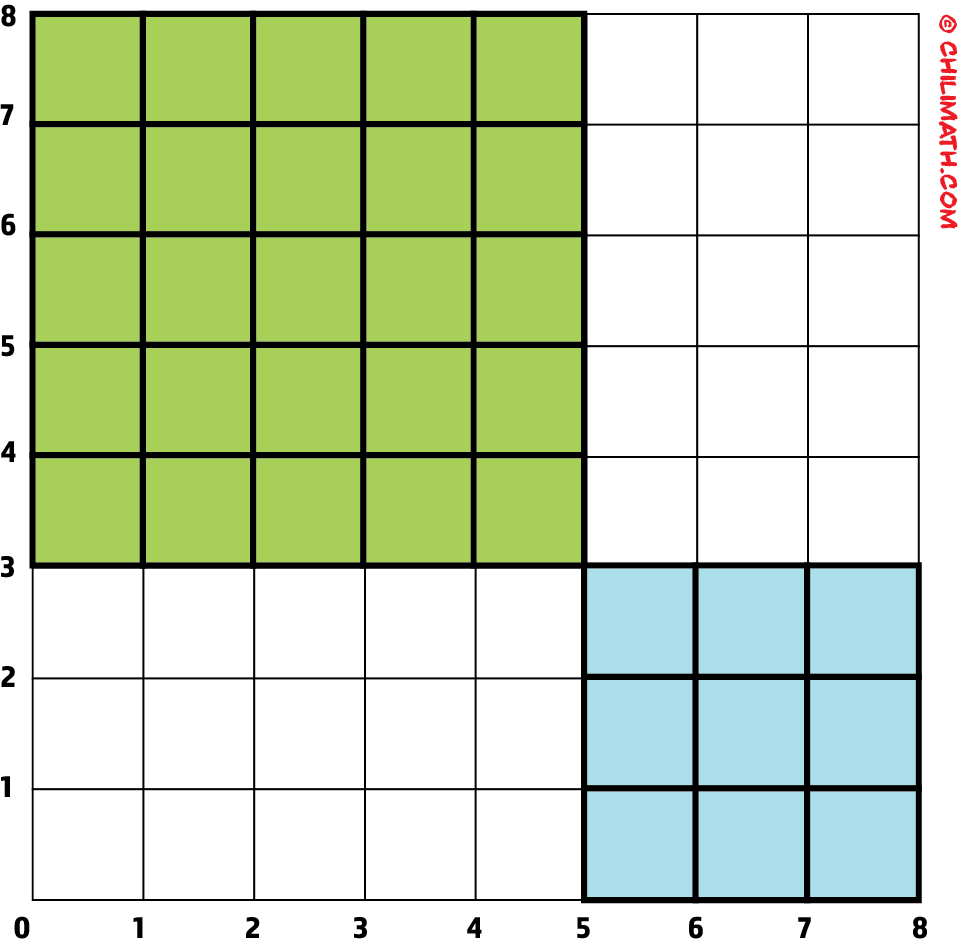
This is a very similar problem to Example 1. The only difference is that we now have two squares instead of one. Since we are interested in finding the total areas of the two squares, we must first determine the area of each square and then add them together to arrive at the final answer.
Let’s count the number of little squares in each huge square, the green and blue squares. Please refer to the diagram below.
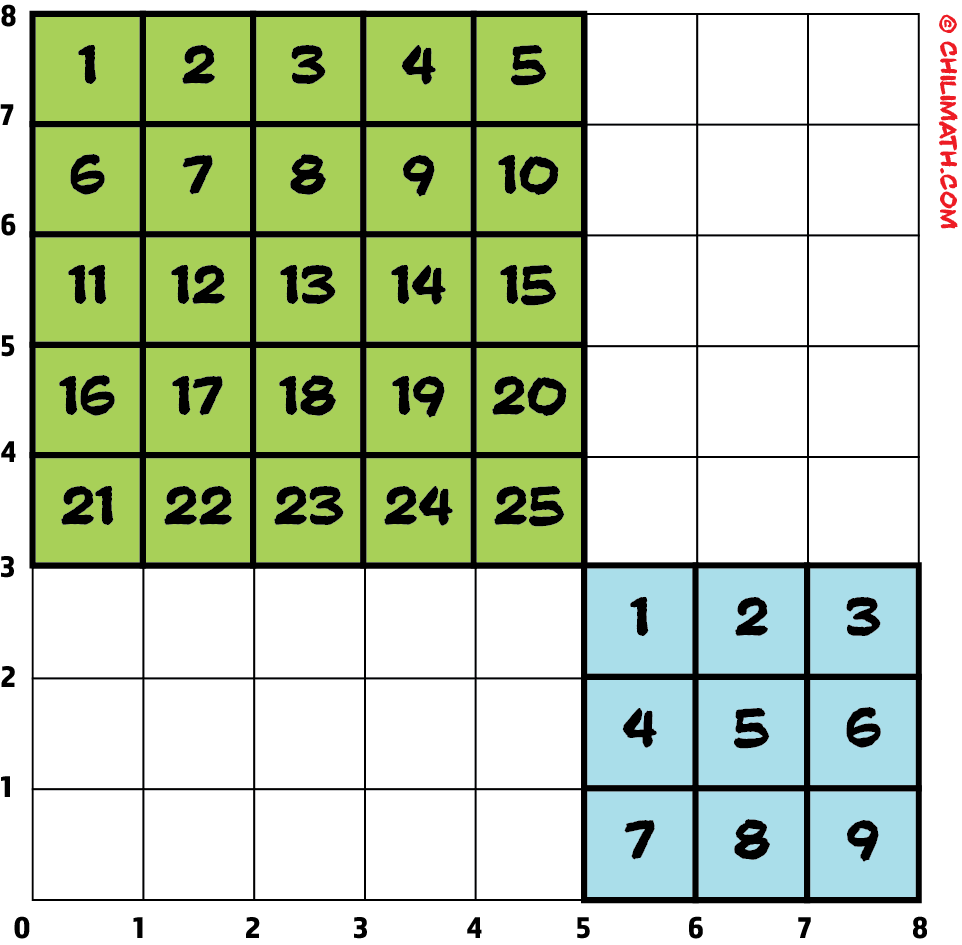
Because the green square comprises 25 little squares, its area is 25 square units. The blue square, on the other hand, has 9 little squares, thus its area is 9 square units. Finally, to get the overall area, add the areas of the green and blue squares which gives us 25 + 9 = 34. Therefore, the total area is 34 square units.
Examples of Finding the Area of Square using its Side
To find the area of a square when the side [latex]s[/latex] is given, simply multiply the side by itself [latex]s \times s[/latex] or square it [latex]s^2[/latex].
Example 3: Find the area of a square whose side length is [latex]7[/latex] [latex]ft[/latex].
A square is a specific case of a rectangle in which the length [latex]l[/latex] and width [latex]w[/latex] are the same. Since the length and width have the same measure, let’s simply call it as side [latex]s[/latex]. Below is the illustration of the given problem. Notice, both sides have the same measure of [latex]7[/latex] [latex]ft[/latex].
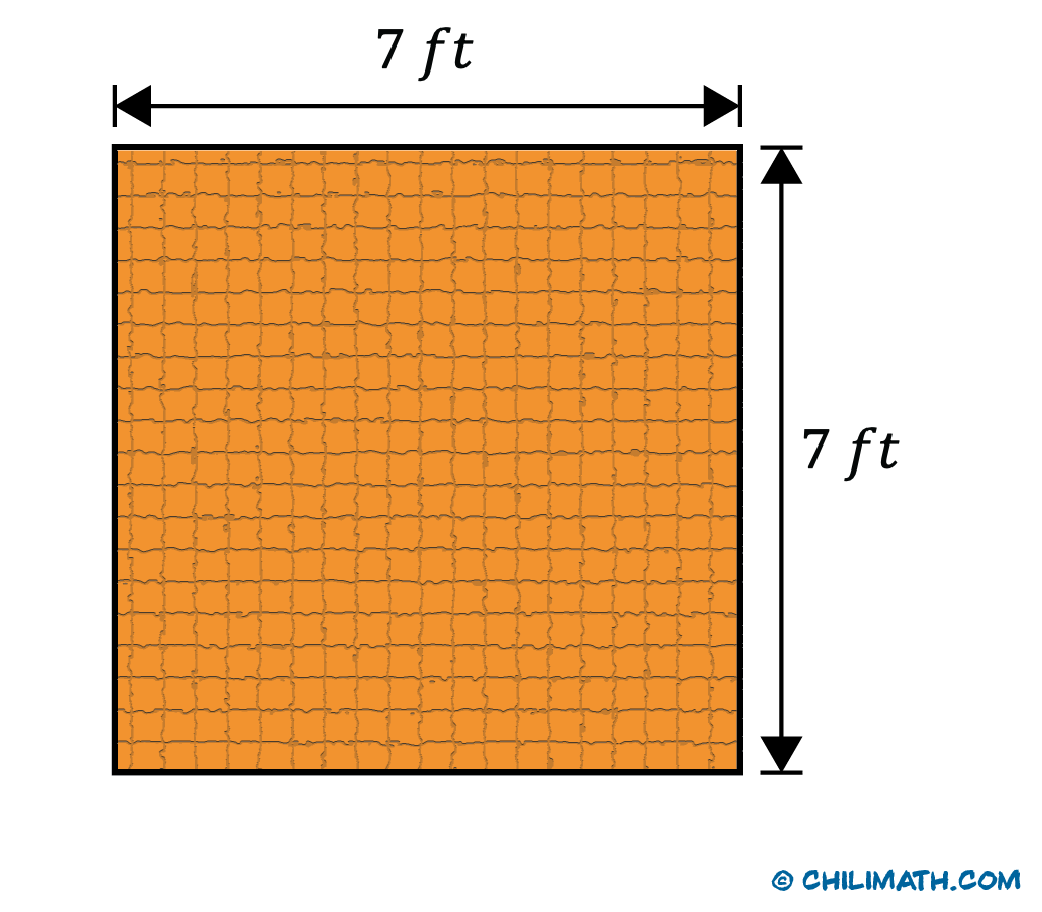
To find the area of the square, we multiply the two sides together.
[latex]A = s \times s = 7 \times 7 = 49[/latex][latex]\,[/latex]unit[latex]^2[/latex]
Or simply square the side. It will have the same result.
[latex]A = {s^2} = {\left( 7 \right)^2} = 49[/latex][latex]\,[/latex]unit[latex]^2[/latex]
Therefore, the area of the square is 49 square units.
Example 4: The side of a square is [latex]1[/latex] yard. What is the area of the square in square inches?
Don’t jump to the conclusion that the solution is [latex]1[/latex] square yard since side times side equals 1, that is, [latex]\left( 1 \right)\left( 1 \right) = 1[/latex]. If the problem is asking for the area in square yards, you are correct. But this is not the case. Clearly, the question is asking for the area in terms of square inches not in square yards.
That is why we must approach each problem with caution. The key is to thoroughly and carefully read the question and to ensure that we understand what is being asked in order to answer the problem correctly!
The first thing we should do is to convert the given unit of measure into the desired unit which is from yard to inch. That means we will have to convert [latex]1[/latex] yard into inches. We know that [latex]1[/latex] yard equals [latex]3[/latex] feet but [latex]1[/latex] foot equals [latex]12[/latex] inches.
Now, let’s convert 1 yard into inches:
[latex]1\,yd\,\, \times \,\,{\Large{{{3\,\,ft} \over {1\,yd}}}}\,\, \times \,\,{\Large{{{12\,\,in.} \over {1\,ft}}}}\,\, = \boxed{\,\,36\,\,in.}[/latex]
Therefore, [latex]1[/latex] yard is equal to [latex]36[/latex] inches.

Upon knowing the side length of the square in terms of inches, we are ready to compute for the area of the square using the formula.
Since the side is [latex]36[/latex] inches, we have
[latex]A = {s^2} = {\left( {36} \right)^2} = 1,296[/latex] [latex]\,[/latex][latex]in^2[/latex]
Therefore, the area of the square is [latex]1,296[/latex] square inches or [latex]\text{in}^2[/latex]
Examples of Finding the Area of Square using its Diagonal
In previous examples, we calculate the area of square using its side [latex]s[/latex]. Is there any other way to find its area other than its side? Well, there is! The fact is, it is possible to solve for the area of square if we know its diagonal. But before I simply give the formula, it is much better if I derive it for you so you can get a better appreciation why it works.
Starting off, let’s derive the formula for calculating a square’s area given its diagonal [latex]d[/latex]. Here we have a square where the sides are labeled as [latex]s[/latex] and the diagonal is labeled as [latex]d[/latex]. Notice that the two sides of the square and its diagonal form a right triangle (a triangle that contains a 90-degree angle).
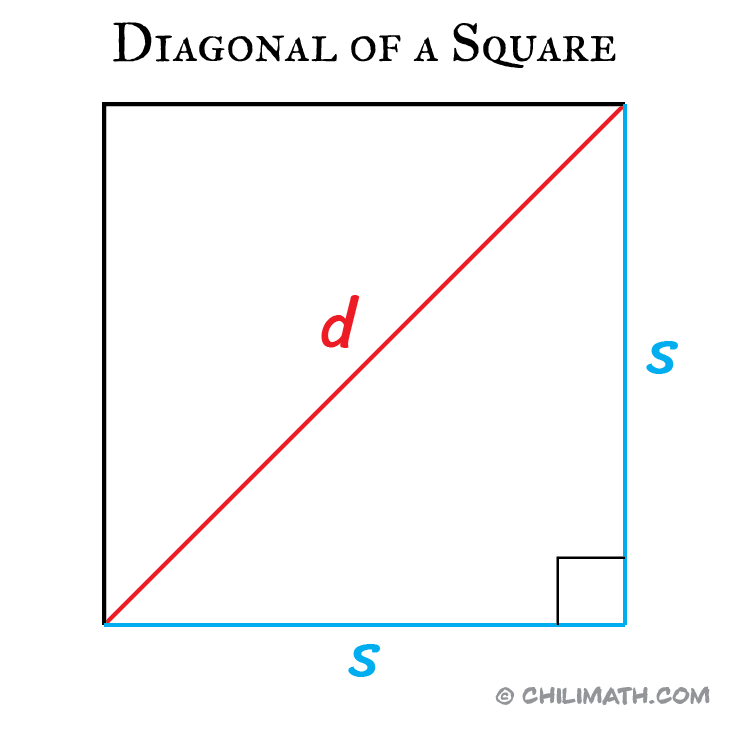
It implies we can mathematically relate the diagonal and the sides of the right triangle in an equation using the Pythagorean Theorem.
The square of the length of the hypotenuse [latex]c[/latex], which is the side opposite the right angle, is equal to the sum of the squares of the lengths of the other two sides which are the legs namely [latex]a[/latex] and [latex]b[/latex].

In our right triangle, the legs have the same side length which is designated by [latex]s[/latex]. In addition, the hypotenuse (the side opposite the 90-degree angle or the longest side) is represented by the letter [latex]d[/latex] to mean diagonal.
Substitute both [latex]a[/latex] and [latex]b[/latex] by [latex]s[/latex], and [latex]c[/latex] by [latex]d[/latex].
Notice below that we combined [latex]s^2[/latex] and [latex]s^2[/latex] to get [latex]2s^2[/latex].
To solve for [latex]s^2[/latex], we divide both sides of the equation by [latex]2[/latex].
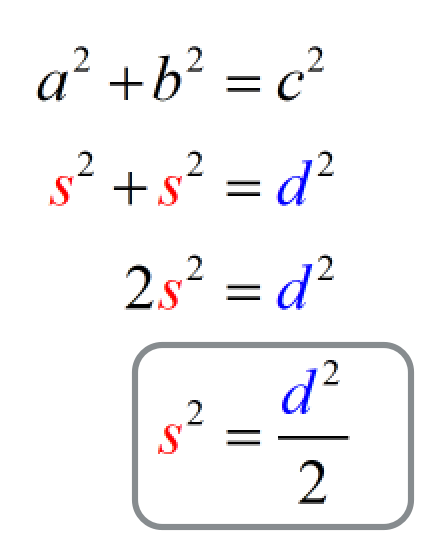
Notice, I didn’t completely solve for [latex]s[/latex] by taking the square root of both sides. I intentionally kept [latex]s^2[/latex] because that is actually what we want since the area of the square is side times side or simply side squared, [latex]s^2[/latex].
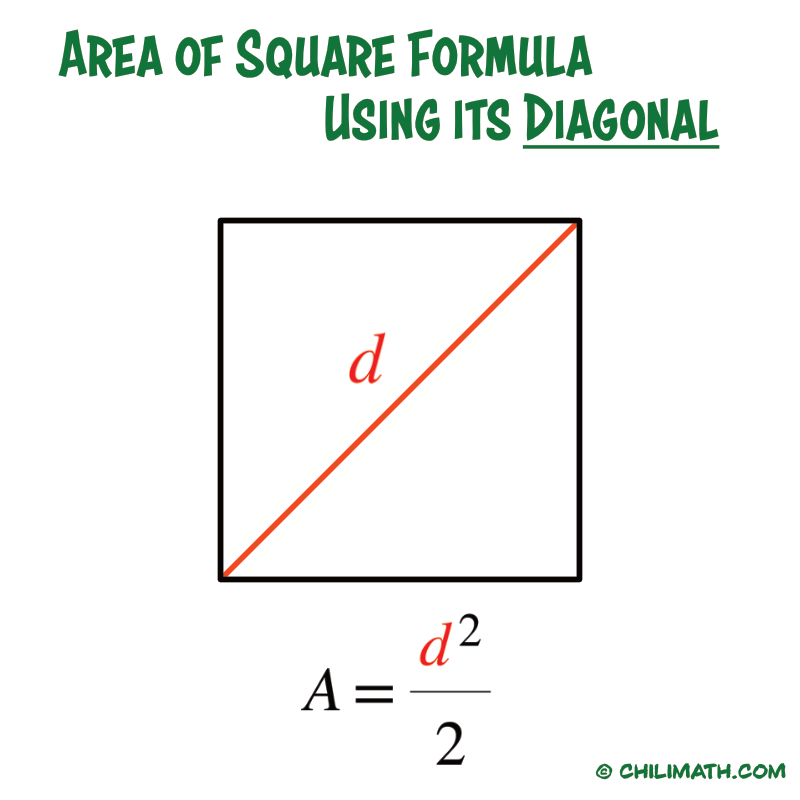
Therefore, an alternative formula to find the area of the square is
[latex]A = {\Large{{{d^2}} \over 2}}[/latex]
where [latex]d[/latex] is the diagonal of the square
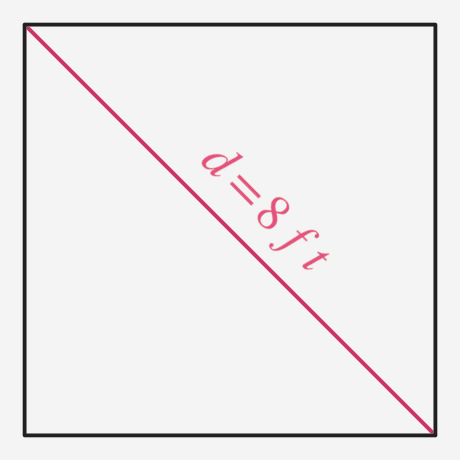
Example 5: What is the area of a square whose diagonal is [latex]8[/latex] [latex]\text{ft}[/latex]?
The good thing is that we have already done the hard work above! We have derived the formula to find the area of a square when the diagonal of the square is given to us.
Since the diagonal is [latex]8[/latex] [latex]\text{ft}[/latex] as you can see in the illustration below, we should be able to find the area of the square by simply substituting the value of the diagonal into the formula and then simplify.
The square of [latex]8[/latex] is [latex]64[/latex]. Then we divide it by [latex]2[/latex] to get [latex]32[/latex].
\begin{align*} A &= {{{d^2}} \over 2} \\ \\ &= {{{{\left( {\color{red}8} \right)}^2}} \over 2} \\ \\ &= {{64} \over 2} \\ \\ A &= 32 \end{align*}Therefore, the area of the square is [latex]32[/latex] [latex]\text{ft}^2[/latex].
The formula above can also be used to calculate the diagonal of a square if we know its area. Let’s look at an example.
Example 6: If the area of a square is [latex]72[/latex] [latex]\text{cm}^2[/latex], what is the length of the diagonal of the square?
Let’s begin by the writing the formula of the area of the square when the diagonal is given.
[latex]\boxed{A = {{{d^2}} \over 2}}[/latex]
Since we know the area of the square, let’s replace [latex]A[/latex] by [latex]72[/latex] on the left side of the equation.
To keep [latex]d^2[/latex] to the right side of the equation, we will multiply [latex]2[/latex] on both sides of the equation.
Finally, to isolate the variable [latex]d[/latex] on the right side we will take the square roots of both sides.
\begin{align*} A &= {{{d^2}} \over 2} \\ \\ 72 &= {{{d^2}} \over 2} \\ \\ \left( {72} \right)2 &= {d^2} \\ \\ 144 &= {d^2} \\ \\ \sqrt {144} &= \sqrt {d^2} \\ \\ \color{red}12 &= d \end{align*}Therefore, the diagonal of the square is [latex]12[/latex] [latex]\text{cm}[/latex].
Examples of Finding the Area of Square using its Perimeter
Now there is a case when we are given the perimeter of the square and we are asked to find its area. How do we do that?
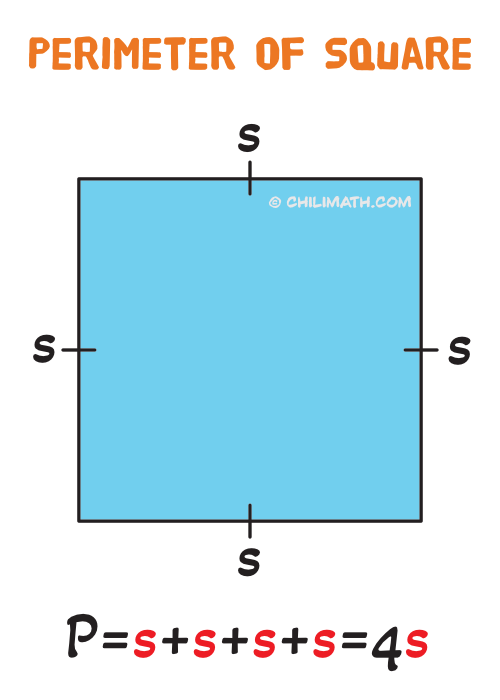
Let’s begin by recalling that the square’s perimeter is merely the sum of all its sides. Since a square is a quadrilateral, it has four (4) sides, so to calculate its perimeter, we must add all four sides together. Moreover, the sides of a square are of equal length. If we let one side to be [latex]s[/latex] then the sum of all four sides must be [latex]s+s+s+s=4s[/latex].
Therefore, the formula for the perimeter of a square is
[latex]\boxed{P = s + s + s + s = 4s}[/latex]
Having learned how to find the square’s perimeter if we know its side, it should be possible to use the same formula to determine the side of the square if the perimeter is given to us.
Looking at the formula again where the perimeter of square is four times its side, [latex]4s[/latex]. The variable [latex]s[/latex] [which is the side of the square] can be solved or isolated by dividing both sides of equation by [latex]4[/latex].
[latex]\boxed{P = 4s}[/latex]
If we divide the entire equation by [latex]4[/latex], we get:
\begin{align*} P &= 4s \\ \\ {P \over 4} &= {{\cancel{4}s} \over \cancel{4}} \\ \\ {P \over 4} &= s \end{align*}Simply put, dividing the perimeter by [latex]4[/latex] will yield the side length of the square. That’s it!
Once we know the measure of one side of the square (note: we only need one since all sides are congruent), we can go back to the basic method for calculating the area of a square, which is side times side [latex]\text{side}[/latex][latex]\times[/latex][latex]\text{side}[/latex] or side squared, [latex]\text{side}^2[/latex].
[latex]\text{Area of Square}\,\square\,[/latex][latex]=[/latex][latex]\,\text{side}[/latex][latex]\times[/latex][latex]\text{side}\,[/latex][latex]=[/latex][latex]\,s^2[/latex]
The best way to illustrate this procedure is through an example!
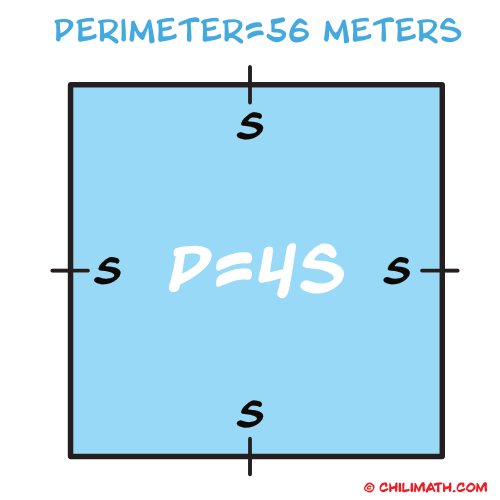
Example 7: Find the area of a square whose perimeter is [latex]56[/latex] meters.
Let’s draw a rough sketch of a square with a perimeter of [latex]56[/latex] [latex]\text{m}[/latex].
Since a perimeter is simply the sum of all sides, and a square has four (4) equal sides, the formula of the perimeter of square must be
[latex]P = s + s + s + s = 4s[/latex]
What we want is to calculate the side of the square given its perimeter. That can be achieved by simply dividing the perimeter by [latex]4[/latex].
\begin{align*} P &= 4s \\ \\ 56 &= 4s \\ \\ {{56} \over 4} &= {{\cancel{4}s} \over \cancel{4}} \\ \\ 14 &= s \end{align*}Upon knowing from our calculation above that the side of the square is [latex]14[/latex] meters, we can now find its area by substituting the measure of the side to the fundamental formula of the area of square which is the square of its side, [latex]s^2[/latex].
\begin{align*} \text{Area of Square} &= {s^2} \\ \\ &= {\left( {\color{red}14} \right)^2} \\ \\ &= {\color{red}14} \times {\color{red}14} \\ \\ \text{Area of Square} &= 196 \end{align*}Therefore, the area of the square is [latex]196[/latex] [latex]\text{m}^2[/latex].
Example 8: What is the area of a square with perimeter [latex]12[/latex] feet?
We should be able to solve this problem very easily with the technique above by simply dividing the given perimeter by [latex]4[/latex] and squaring the quotient to get the area of the square.
But let’s derive a much simpler formula that we can add in our math toolbox.
Remember, if we know the perimeter of the square, we can divide by [latex]4[/latex] to get the measure of the side of the square.
\begin{align*} P &= 4s \\ \\ {P \over 4} &= {{\cancel{4}s} \over \cancel{4}} \\ \\ {P \over 4} &= s \end{align*}That means, if we square both sides of the equation, the right side becomes [latex]s^2[/latex] which is literally the area of the square. In other words, we can also determine the area of square by squaring the perimeter and dividing it by [latex]16[/latex].
\begin{align*} {\left( {{P \over 4}} \right)^2} &= {\left( s \right)^2} \\ \\ {{{P^2}} \over {16}} &= {s^2} \end{align*}Thus, a much simpler formula to find the area of a square when its perimeter is known:
[latex]\boxed{A = {{{P^2}} \over {16}}}[/latex]
So, if a square has perimeter of [latex]12[/latex] feet, its area must be
\begin{align*} A &= {{{P^2}} \over {16}} \\ \\ &= {{{\left( {12} \right)} \over {16}}^2} \\ \\ &= {{144} \over {16}} \\ \\ A &= 9 \end{align*}Therefore, the area of the square is [latex]9[/latex] [latex]\text{ft}^2[/latex].
