Corresponding Angles

Corresponding angles are two angles that lie in similar relative positions on the same side of a transversal or at each intersection. They are usually formed when two parallel or non-parallel lines are cut by a transversal.

Remember that a transversal is a line that intersects two or more lines.

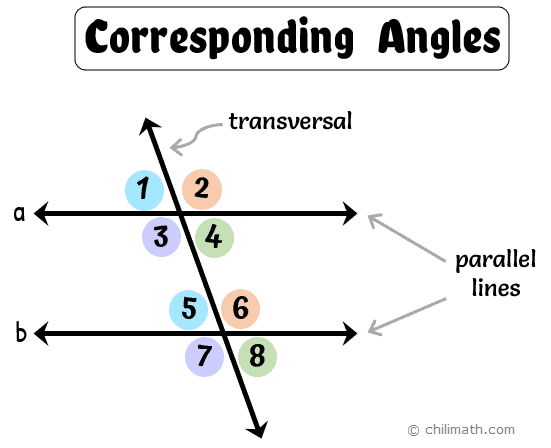
parallel lines a and b cut by a transversal forming four corresponding angles

In our illustration above, parallel lines [latex]a[/latex] and [latex]b[/latex] are cut by a transversal which as a result, formed 4 corresponding angles. For example, [latex]\angle 2[/latex] and [latex]\angle 6[/latex] are corresponding angles. Why? Because both angles are located in matching corners or corresponding positions on the right-hand side of the transversal. In other words, each angle is located above the line and to the right of the transversal.

Here are our corresponding angles (must be in pairs) from the diagram and their location.

  • [latex]\angle \textbf{1}[/latex] and [latex]\angle \textbf{5}[/latex] – above the line, left of the transversal
  • [latex]\angle \textbf{3}[/latex] and [latex]\angle \textbf{7}[/latex] – below the line, left of the transversal
  • [latex]\angle \textbf{2}[/latex] and [latex]\angle \textbf{6}[/latex] – above the line, right of the transversal
  • [latex]\angle \textbf{4}[/latex] and [latex]\angle \textbf{8}[/latex] – below the line, right of the transversal

There are a few things to remember when dealing with corresponding angles.

Corresponding Angles Postulate

When two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent or have the same measure.

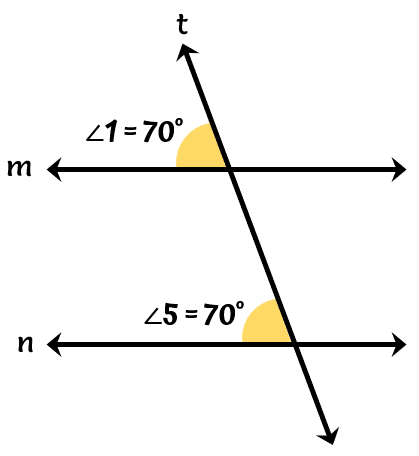
angle 1 and angle 5 are in corresponding positions and therefore have equal measures of 70 degrees

Take for example in our diagram above, since [latex]\angle 1[/latex] and [latex]\angle 5[/latex] are corresponding angles, they are congruent. This also means that if [latex]\angle 1[/latex] measures [latex]70^\circ [/latex] then [latex]\angle 5[/latex] also measures [latex]70^\circ [/latex]. Therefore, [latex]\angle 1 \cong \angle 5[/latex].

On the other hand, if the transversal intersects with two non-parallel lines, the corresponding angles formed are not congruent and do not have a specific relationship to each other.

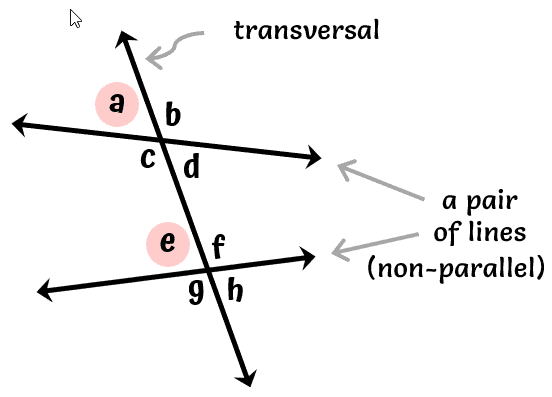
a pair of non-parallel lines cut by a transversal forming four corresponding angles such as angle a and e

Hence, [latex]\angle a[/latex] and [latex]\angle e[/latex] are corresponding angles but are NOT congruent.

Example Problems Involving Corresponding Angles

Example 1: Identify the corresponding angles.

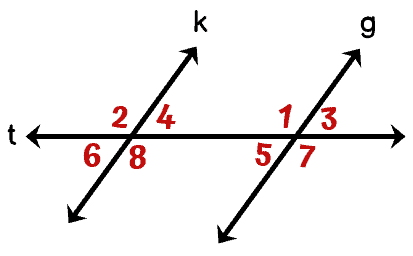
parallel lines k and g cut by a transversal, t. angles 2, 4, 1, and 3 on the right side of the transversal while angles 6, 8, 5, and 7 on the right-hand side of a transversal

Here we have two parallel lines, lines [latex]k[/latex] and [latex]g[/latex], that are cut by the transversal, [latex]t[/latex]. Remember that corresponding angles are angles that are in similar positions on the same side of the transversal.

So the corresponding angles are:

  • [latex]\angle 2[/latex] and [latex]\angle 1[/latex]
  • [latex]\angle 4[/latex] and [latex]\angle 3[/latex]
  • [latex]\angle 6[/latex] and [latex]\angle 5[/latex]
  • [latex]\angle 8[/latex] and [latex]\angle 7[/latex]

Example 2: Name the pairs of corresponding angles and their location.

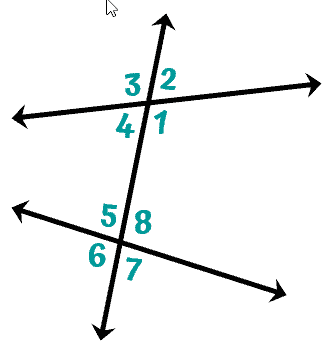
two non-parallel lines intersected by a transversal with angles 3, 4, 5, and 6 on the left side of the transversal while angles 2, 1, 8, and 7 are on the right side of the transversal

As you can see, the transversal cuts across two non-parallel lines forming 4 corresponding angles. Always remember that in this case, though the angles are located in corresponding positions relative to the two lines, they are not congruent.

The corresponding angles are:

  • [latex]\angle 3[/latex] and [latex]\angle 5[/latex] – above the line, left of the transversal
  • [latex]\angle 4[/latex] and [latex]\angle 6[/latex] – below the line, left of the transversal
  • [latex]\angle 2[/latex] and [latex]\angle 8[/latex] – above the line, right of the transversal
  • [latex]\angle 1[/latex] and [latex]\angle 7[/latex] – below the line, right of the transversal

Example 3: Find the measure of [latex]\angle 8[/latex].

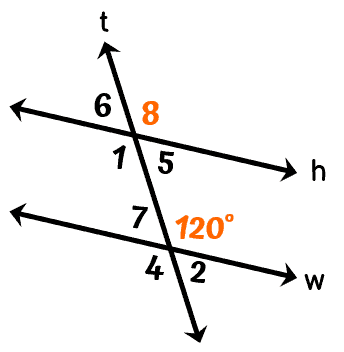
lines h and w are parallel cut by a transversal, t. angle 8 is located above the line and to the right of the transversal

Since line [latex]h[/latex] and line [latex]w[/latex] are parallel lines, the measure of [latex]\angle 8[/latex] should be the same as its corresponding angle. Hence, the [latex]m\angle 8[/latex] is [latex]120^\circ[/latex].

You may also be interested in these related math lessons or tutorials:

Alternate Exterior Angles

Alternate Interior Angles

Complementary Angles

Supplementary Angles

Vertical Angles