Complementary Angles
Two positive angles are complementary if their angle measures sum up to [latex]90^\circ [/latex]. When they are adjacent to each other, you’ll realize that they form a right angle. A right angle measures exactly [latex]90^\circ [/latex], so are complementary angles.
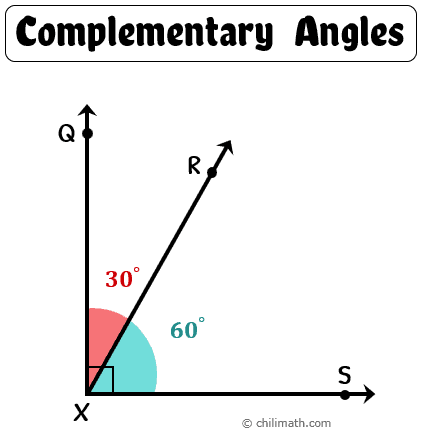
In our illustration above, [latex]\angle QXR[/latex] and [latex]\angle RXS[/latex] are complementary. Why? Because these two angles complement each other with their angle measures adding up to [latex]90^\circ [/latex].
However, two angles don’t need to be adjacent or have a common side and vertex to be called complementary angles. If their angle measures add up to [latex]90^\circ [/latex], they are also complementary.
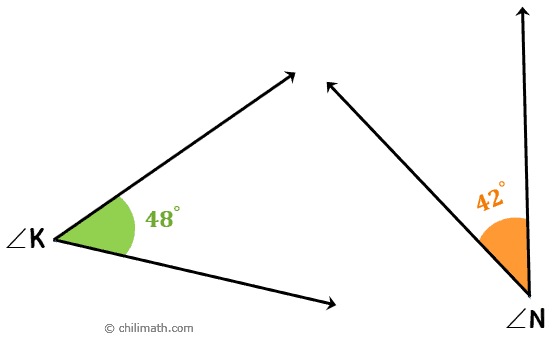
Above we have two non-adjacent angles, [latex]\angle K[/latex] and [latex]\angle N[/latex]. But since the [latex]m\angle K = 48^\circ [/latex] and [latex]m\angle N = 42^\circ [/latex] add up to [latex]90^\circ [/latex], they are also called complementary angles.
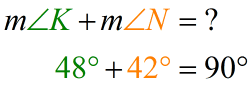
Tip: Be careful to spell it as “complement”, with an “e”, and NOT as “compliment”. However, I’m sure you’ll be getting a lot of compliments if you spell it correctly each time.
Example Problems Involving Complementary Angles
The best way to get familiar with the relationship of this angle pair is by going through various examples.
Example 1: What is the measure of [latex]\angle EHF[/latex]?
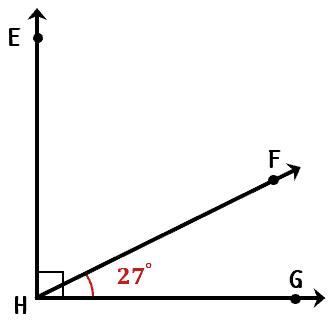
Here we have two complementary angles that are next to each other forming the right angle, [latex]\angle EHG[/latex]. However, we are only given the angle measure of [latex]\angle FHG[/latex] which is [latex]27^\circ [/latex].
Since we know that right angles measure exactly [latex]90^\circ [/latex], then it’s safe to say that the measures of [latex]\angle EHF[/latex] and [latex]\angle FHG[/latex] sum up to [latex]90^\circ [/latex]. We’ll use this concept to set up our equation and use the variable [latex]x[/latex] in place of the missing angle measure.
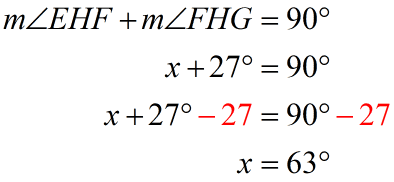
So we have [latex]x = 63[/latex] which means that the measure of [latex]\angle EHF[/latex] is [latex]\textbf{63}^\circ[/latex].
To check if our answer is correct, all we have to do is plug in the value of [latex]x[/latex] into our original equation. If both sides of the equation equal to [latex]90[/latex], then we got the correct measure for [latex]\angle EHF[/latex].
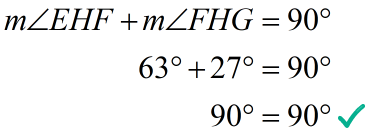
Example 2: Are [latex]\angle LMP[/latex] and [latex]\angle UVW[/latex] complementary?
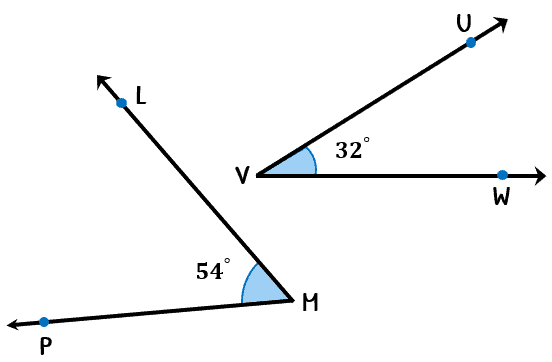
At the beginning of this lesson, we discussed that angles don’t have to share the same side or vertex (adjacent) in order to be called complementary angles. If their measures sum up to [latex]90^\circ [/latex], they are still considered as complementary.
So all we have to do in this example is add the measures of both angles to find out if the total comes up to [latex]90^\circ [/latex].
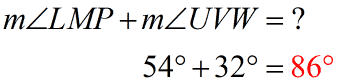
Unfortunately, the measures of our angles did not add up to [latex]90^\circ [/latex]. Therefore, [latex]\angle LMP[/latex] and [latex]\angle UVW[/latex] are NOT complementary angles.
Example 3: Find the missing angle measure.
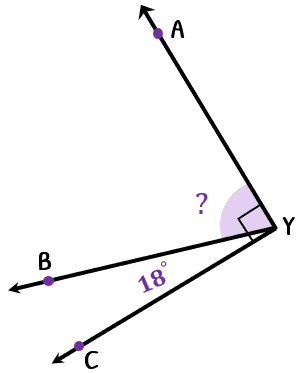
This problem is similar to our first example. We are again given a right angle formed by two adjacent and complementary angles, namely, [latex]\angle AYB[/latex] and [latex]\angle BYC[/latex]. Always remember that a right angle measures [latex]90^\circ [/latex].
This time, instead of setting up an equation, let’s simply subtract the known measure ([latex]18^\circ [/latex]) from [latex]90^\circ [/latex] to find the missing measure for [latex]\angle AYB[/latex].
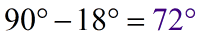
Is this correct? Well, the only way to find out is by checking if [latex]18^\circ [/latex] and [latex]72^\circ [/latex] add up to [latex]90^\circ [/latex].
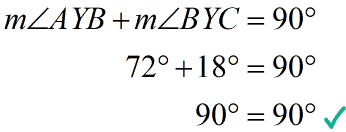
And they do! So, the missing angle measure or the [latex]m\angle AYB[/latex] is [latex]\textbf{72}^\circ [/latex].
Example 4: If [latex]\angle J[/latex] and [latex]\angle T[/latex] are complementary and [latex]\angle J[/latex] is [latex]33^\circ [/latex], what is the measure of [latex]\angle T[/latex]?
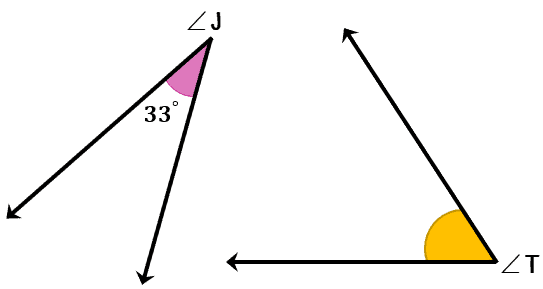
In this example, we are given two separate angles but their measures should total to [latex]90^\circ [/latex] because they are complementary. Since we already have the measure for [latex]\angle J[/latex], we’ll proceed by merely subtracting [latex]33^\circ [/latex] from [latex]90^\circ [/latex]. Their difference would be the angle measure for [latex]\angle T[/latex].
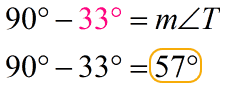
We get [latex]\textbf{57}^\circ [/latex] as the measure for [latex]\angle T[/latex].
Let’s now add [latex]57^\circ [/latex] and [latex]33^\circ [/latex] to check if their measures sum up to [latex]90^\circ [/latex].
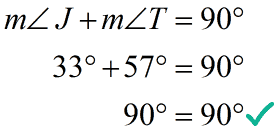
Example 5: Find the value of [latex]x[/latex].
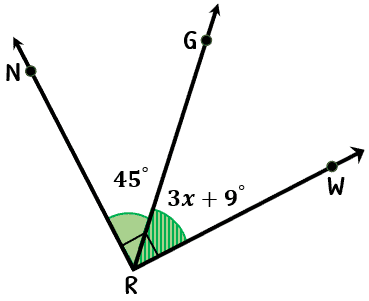
The diagram gives us two angle measures with one of the measures expressed in an algebraic expression. It may look challenging but it’s actually not. As long as you know the concept of the relationship between complementary angles, you’ll be fine.
By now we know that the sum of the measures will be [latex]90^\circ [/latex]. So we’ll set up our equation by adding both measures on one side of the equation and [latex]90^\circ [/latex] on the other.
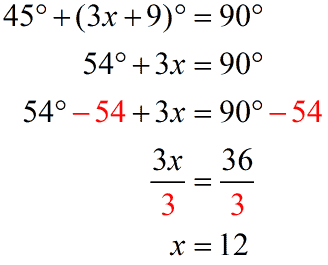
The value of [latex]x[/latex] is [latex]\textbf{12}[/latex].
However, since we already know what [latex]x[/latex] is, we might as well find out what the measure of [latex]\angle GRW[/latex] is since it is expressed in an algebraic expression.
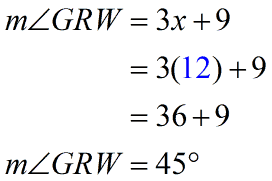
Awesome! The measure of [latex]\angle GRW[/latex] is also [latex]45^\circ [/latex]!
Is that really correct? Well, simply add [latex]45^\circ [/latex] and [latex]45^\circ [/latex]. Both measures should total to [latex]90^\circ [/latex].
Example 6: What is the value of [latex]x[/latex]?
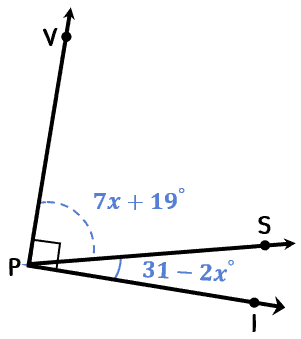
This next example is interesting because now both angle measures are expressed in algebraic expressions. But as I said before, just always remember that the sum of their measures will be [latex]90^\circ [/latex] since they are complementary angles. With that in mind, it’ll be easy for you to set up our equation and solve for [latex]x[/latex].
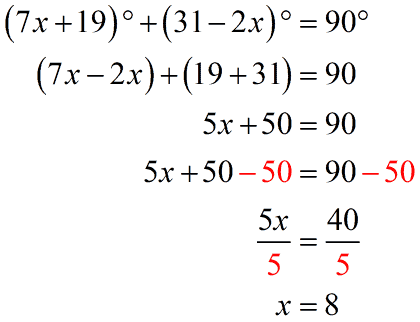
The value of [latex]x[/latex] is [latex]\textbf{8}[/latex].
Let’s use this value to find out what our angle measures are.

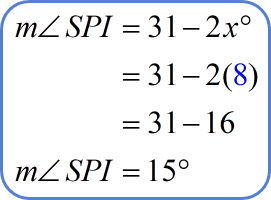
There you have it. We have [latex]75^\circ [/latex] and [latex]15^\circ [/latex] as our angle measures. I’ll now leave it up to you to check if these measures actually sum up to [latex]90^\circ [/latex].
Example 7: Suppose [latex]\angle AKL[/latex] and [latex]\angle QBH[/latex] are complementary. Find the measures of the two angles.
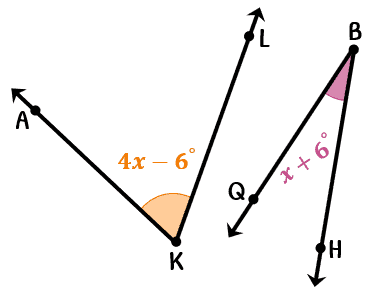
Note that even though they are two separate angles, they are complementary. Hence, their angle measures should sum up to [latex]90^\circ [/latex].
We’ll now find what these measures are by first solving for [latex]x[/latex].
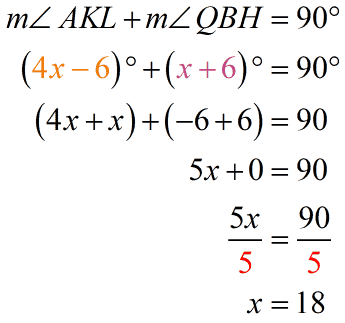
So we have [latex]x = 18[/latex]. Let’s continue finding the measures for [latex]\angle AKL[/latex] and [latex]\angle QBH[/latex].
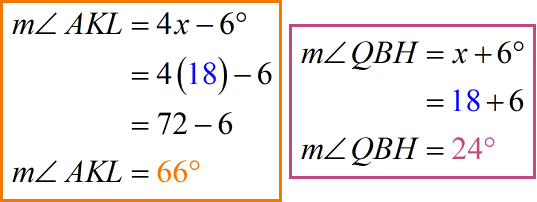
If we add both angle measures, [latex]\textbf{66}^\circ + \textbf{24}^\circ = 90^\circ[/latex], indeed they are complementary angles.
Example 8: Determine the measures of the two complementary angles.
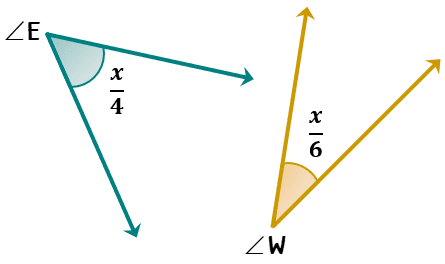
We have another interesting example here. Instead of algebraic expressions, our angle measures are now expressed as fractions. Let’s apply the same strategies that we used in our previous examples.
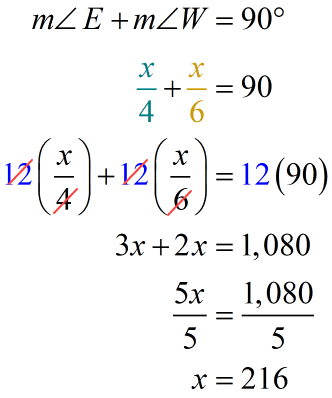
To find the [latex]m\angle \,E[/latex] and [latex]m\angle \,W[/latex], we’ll simply substitute [latex]x[/latex] with 216.
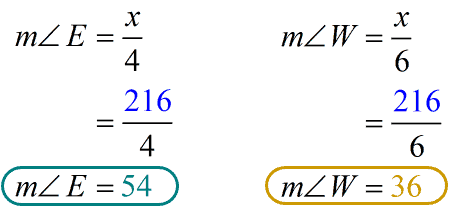
Both measures sum up to [latex]90^\circ [/latex] which confirms that both angles are complementary.
Example 9: Two complementary angles are such that one of the angles is twice the sum of the other angle. What are the measures of the complementary angles?
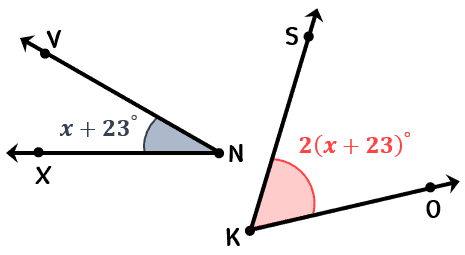
Begin by solving for [latex]x[/latex].
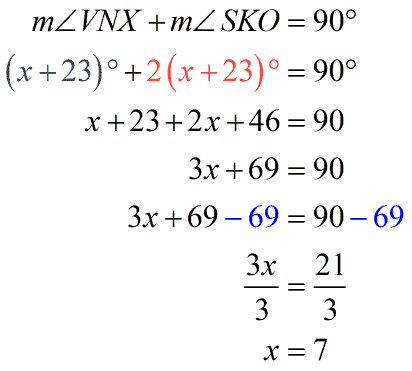
This time, I’ll let you find the measures for [latex]\angle VNX[/latex] and [latex]\angle SKO[/latex]. If you solved them correctly, below are the measures that you should get.
[latex]m\angle VNX = 30^\circ[/latex]
[latex]m\angle SKO = 60^\circ [/latex]
Example 10: [latex]\angle MJC[/latex] is a right angle. If the measure of [latex]\angle MJT[/latex] is [latex]4 + 3x^\circ[/latex] and the measure of [latex]\angle TJC[/latex] is [latex]5x + 14^\circ[/latex], what is the measure of [latex]\angle TJC[/latex]?
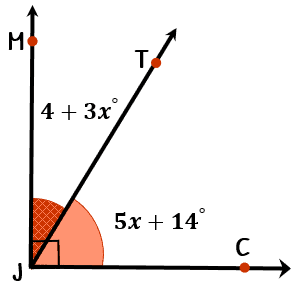
Here’s another practice for you! Try solving this on your own first. Then check your answers by simply clicking the colored bar below.
Check answer for [latex]m\angle TJC[/latex]
Value of [latex]x[/latex]= [latex]9[/latex]
[latex]m\angle MJT = 31^\circ[/latex]
[latex]m\angle TJC =\textbf{59}^\circ[/latex]
You may also be interested in these related math lessons or tutorials:
