Alternate Exterior Angles
The pair of non-adjacent angles on the outer side or “outside” of the two lines but on opposite sides of the transversal are known as alternate exterior angles.
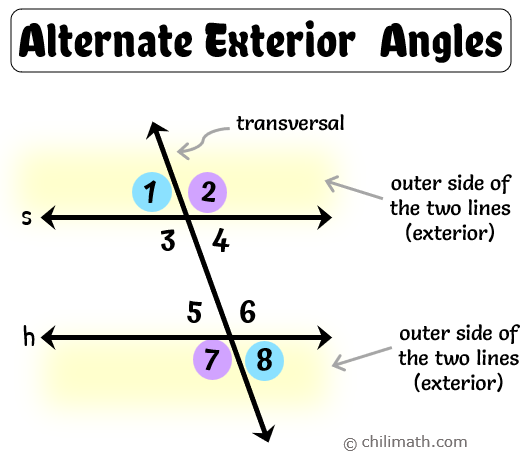
When two parallel or non-parallel lines are intersected by a transversal, they usually form eight (8) angles. Exterior angles are the angles that exist outside of the two lines. But when it comes to pairs of alternate exterior angles, keep in mind that they are not only on opposite sides of the transversal but also outside of the two lines.
In our illustration above, [latex]\angle 1[/latex] and [latex]\angle 8[/latex] are a pair of alternate exterior angles. Why? Because both angles are located outside lines [latex]s[/latex] and [latex]h[/latex], are not adjacent to each other, and are on opposite sides of the transversal. The other pair of alternate exterior angles are [latex]\angle 2[/latex] and [latex]\angle 7[/latex].
Alternate Exterior Angles Theorem
If two parallel lines are cut by a transversal, then the pairs of alternate exterior angles are congruent.
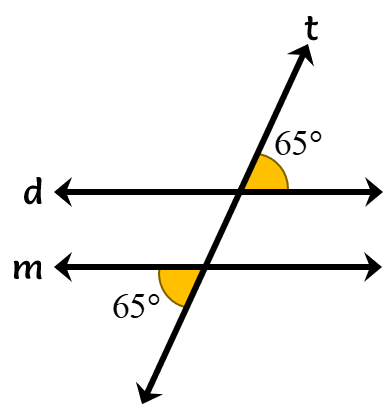
This illustration shows lines, [latex]d[/latex] and [latex]m[/latex], being intersected by the transversal, [latex]t[/latex]. Since lines [latex]d[/latex] and [latex]m[/latex] are parallel lines, the alternate exterior angles formed are congruent which means they have the same measure.
Conversely, alternate exterior angles are not congruent and do not have a relationship if two non-parallel lines are cut by a transversal.
Example Problems Involving Alternate Interior Angles
Example 1: Identify all pairs of alternate exterior angles.
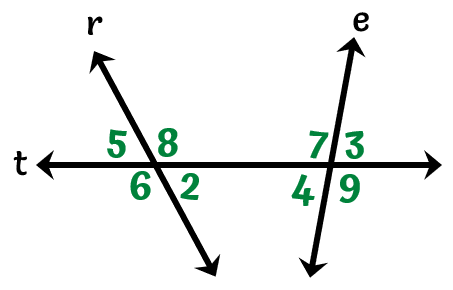
First, we need to pick out our exterior angles. We see that [latex]\angle 5[/latex], [latex]\angle 6[/latex], [latex]\angle 3[/latex], and [latex]\angle 9[/latex] are all located outside lines [latex]r[/latex] and [latex]e[/latex].
However, since we are asked to list the alternate exterior angles, we need to look at the pairs of angles that are not adjacent to each other and are located on opposite sides of the transversal, [latex]t[/latex].
Therefore, our alternate exterior angles are:
- [latex]\angle 5[/latex] and [latex]\angle 9[/latex]
- [latex]\angle 6[/latex] and [latex]\angle 3[/latex]
Example 2: Determine if the following statements are True or False.
- When two non-parallel lines are cut by a transversal, the alternate exterior angles formed are congruent.
Answer: FALSE. Alternate exterior angles are not congruent and have no relationship in any way when a transversal cuts two non-parallel lines.
- Alternate exterior angles are congruent when a transversal intersects two parallel lines.
Answer: TRUE. Alternate exterior angles are only of the same measure if the lines cut through by a transversal are parallel.
Example 3: What is the measure of [latex]\angle 5[/latex]?
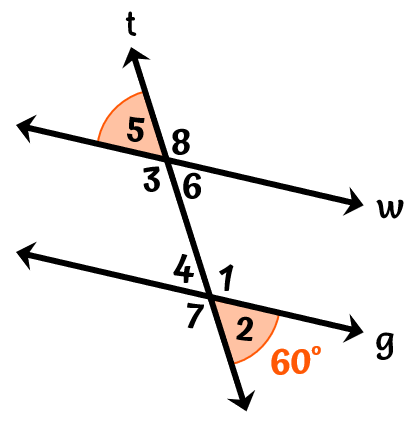
Right off the bat, we see that [latex]\angle 5[/latex] and [latex]\angle 2[/latex] are a pair of alternate exterior angles. And since line [latex]w[/latex] and line [latex]g[/latex] are parallel lines cut by the transversal, [latex]t[/latex], then the two angles are congruent or their measures are the same.
Given that the measure of [latex]\angle 2[/latex] is [latex]60^\circ[/latex], we can conclude that the measure of [latex]\angle 5[/latex] is also [latex]60^\circ[/latex].
You may also be interested in these related math lessons or tutorials:
