Circumference of Circle Formula
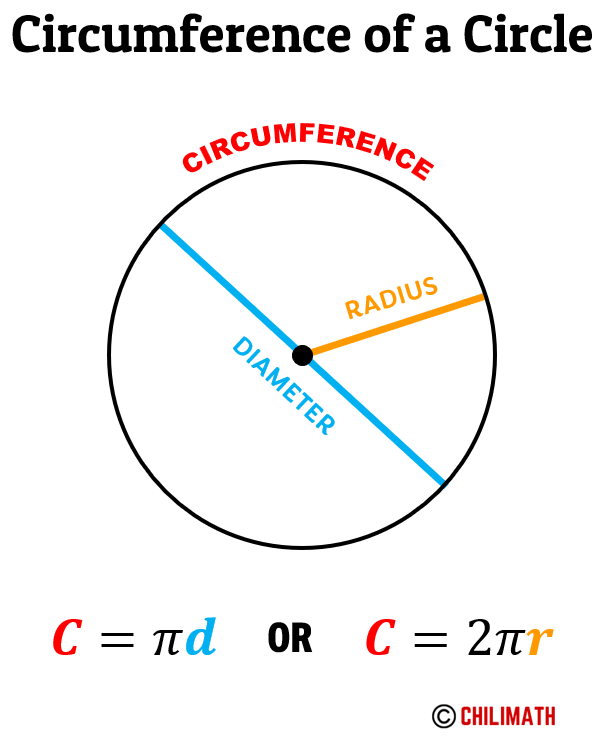
The circumference of a circle is the measurement of how far the distance goes around the circle. We can think of it as the “perimeter” of the circle because it is literally the measure of the length of the circle’s boundary.
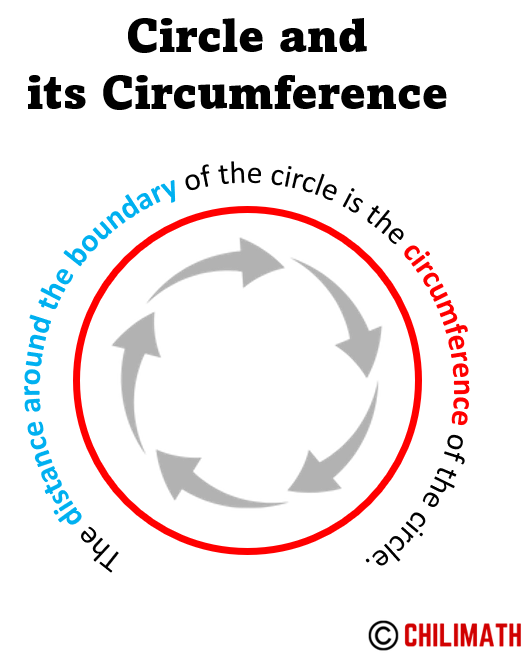
So if you have a circle made up of a piece of thread and you cut it, and you measure its length using a straight edge like a ruler, you are actually measuring the circumference of the circle.

The circumference of a circle is comparable to a rectangle’s perimeter. Recall that the perimeter of a rectangle may be calculated by adding all the sides of the rectangle, that is, the sum of twice the length and twice the width. Hence, the circumference of a circle is also referred to as the perimeter of the circle.
The Formula of the Circumference of Circle
The circumference, [latex]C[/latex], of a circle is calculated by multiplying pi [latex]\color{blue}\large{\pi}[/latex] by the diameter [latex]\color{red}\large{d}[/latex].
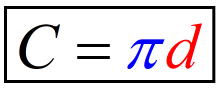
Alternatively, since the diameter is twice the value of radius [latex]\large{2\color{red}r}[/latex] then we can rewrite the formula above as:
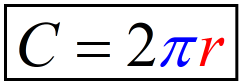
By the way, the commonly used values for the irrational number [latex]\large{\pi}[/latex] are the following:
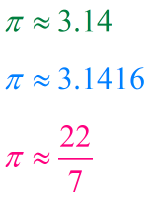
Examples of Finding the Circumference of a Circle
Example 1: Find the circumference of a circle whose radius is [latex]3[/latex] feet. Use [latex]\pi = 3.1416[/latex]. Round your answer to the nearest hundredth.
We can easily substitute the value of radius value into the formula because it is clearly given to us. However, it’s important to keep in mind that we have been specifically instructed to utilize the approximate value of [latex]\pi [/latex], which in this case is [latex]3.1416[/latex]. Our final answer should be rounded off to two decimal places as well.

Therefore, the circumference of the circle is [latex]18.85[/latex] feet.
Example 2: The diameter of the circle is [latex]12[/latex] inches. Find its circumference. Use [latex]\pi = 3.14[/latex]. Round your answer to the nearest tenth.
This is an excellent example of a math problem that can be perfectly solved in two (2) ways. The first method is to use the standard formula of the circumference of a circle, where we need to convert the given diameter into the radius. The second method is to perform a direct substitution of the diameter into the formula [latex]C = \pi d[/latex].
[latex]\odot[/latex] First Method: Using radius [latex]r[/latex]
Since the diameter is [latex]12[/latex], we divide it by [latex]2[/latex] to get the radius. For now, let’s ignore the unit of measurement. Thus,
[latex]r = {\Large{{d \over 2} = {{12} \over 2}}} ={ \color{red}6}[/latex]
Now we can plug in the value of radius into the formula then simplify. Make sure to round your answer to the nearest tenth.

[latex]\odot[/latex] Second Method: Using diameter [latex]d[/latex]
We can use the formula of the circumference with the diameter as the input value. Just direct substitute the length of the diameter which is [latex]12[/latex], then simplify. Don’t forget to round your answer to one decimal place (nearest tenth).
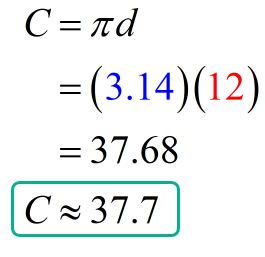
We solved the problem using two different approaches, but both led to the same result. Therefore, the circumference of the circle is [latex]37.7[/latex] inches.
Example 3: Find the exact circumference of the given circle below.

In this problem, we are asked to calculate the exact circumference of the circle given the length of the radius. What this means is that we will leave our answer in terms of pi [latex]\pi[/latex]. In other words, we will not use any approximate value of [latex]\pi[/latex] to compute the circumference.
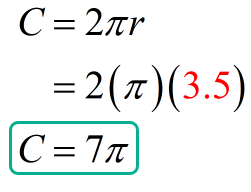
Therefore, the circumference of the circle is [latex]7\pi [/latex] centimeters.
Example 4: Determine the circumference of the circle below using the endpoints of the diameter as shown in red dots. Use [latex]\pi = 3.14[/latex]. Round your answer to the nearest whole number.
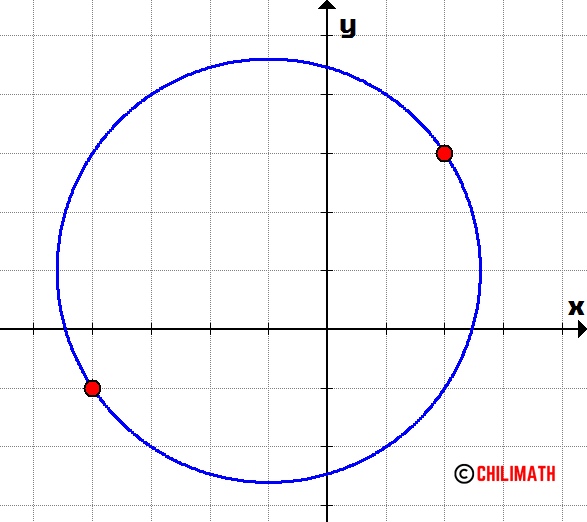
The first step is to describe the ordered pairs of the diameter’s endpoints. Observe that each tick mark is one unit. To describe the left endpoint, we go [latex]4 [/latex] units to the left then [latex]1[/latex] unit down, therefore we have [latex]\left( { – 4, – 1} \right)[/latex]. In addition, to describe the right endpoint, we go [latex]2[/latex] units to the right then [latex]3[/latex] units up, therefore we have [latex]\left( {2,3} \right)[/latex].
Here are our ordered pairs on the XY-axis.
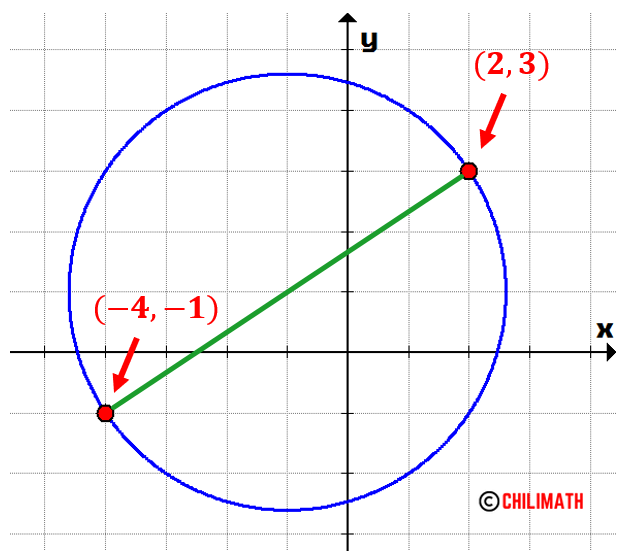
The next step is to find the length of the diameter using the two points we just found which are [latex]\left( { – 4, – 1} \right)[/latex] and [latex]\left( {2,3} \right)[/latex].
Now, let’s use the Distance Formula to calculate the length of the diameter. Setting up our first and second points, we have:

We substitute the values into the Distance Formula and then simplify, we get
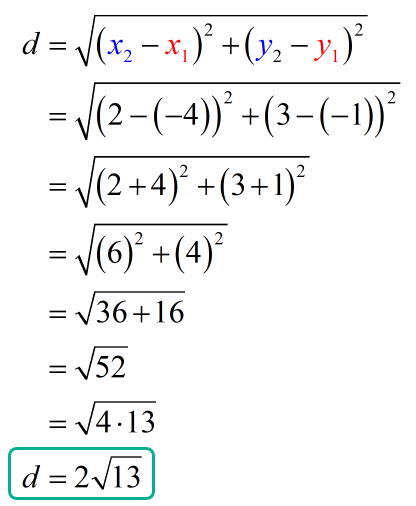
Since we already know what the diameter of the circle is, the radius can simply be found by dividing it by [latex]2[/latex].
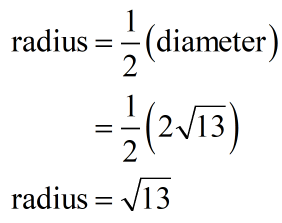
Upon knowing the value of the radius which is [latex]\sqrt {13}[/latex], we are now ready to plug this into the circumference formula. Make sure to use [latex]\pi = 3.14[/latex] as instructed in the problem, and to round off the final answer to the nearest whole number.
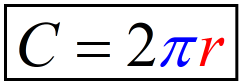
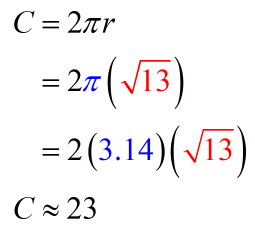
Therefore, the circumference of the circle is [latex]23[/latex].
Example 5: Find the radius of a circle with a circumference of [latex]13\pi [/latex].
This particular kind of problem is a little bit different. The question does not ask us to determine the circumference of the circle; rather, it is interested in the circle’s radius. When you really break it down, the formula for calculating the circumference of a circle is quite straightforward. It contains two unknowns – namely, the circumference [latex]C[/latex] and radius [latex]r[/latex]. If we know one of the two variables, we can easily solve for the other. In this case, we know the value of the circumference, which means we can solve for the radius.

Let’s plug in the value of the circumference into the formula and solve the value of the radius. Notice that [latex]\pi[/latex] will simply out cancel here.
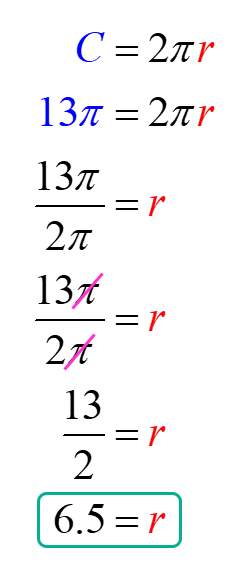
Therefore, the radius of the circle is [latex]6.5[/latex].
Example 6: Find the circumference of the circle below. Use [latex]\pi = {{22} \over 7}[/latex]. Round your answer to the nearest hundredth.
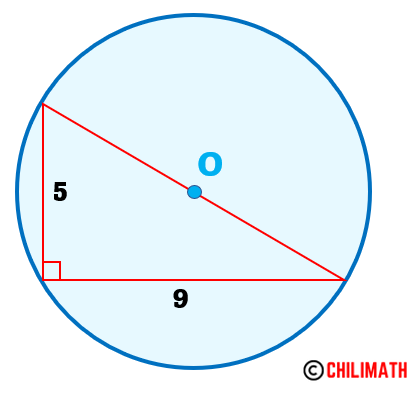
When you take a quick look, you should notice that there is a triangle contained within a circle. We say that the triangle is inscribed in a circle. Given that one of the triangle’s angles measures 90 degrees, we know that the triangle inside the circle is a right triangle.
Remember, we want to find the circumference of the circle. That means we need to either have the radius or the diameter of the circle.
Notice that the hypotenuse (longest side) of the right triangle acts as the diameter of the circle. Since we know the measures of the two other sides (legs), we should be able to calculate the hypotenuse or the diameter using the Pythagorean Theorem.
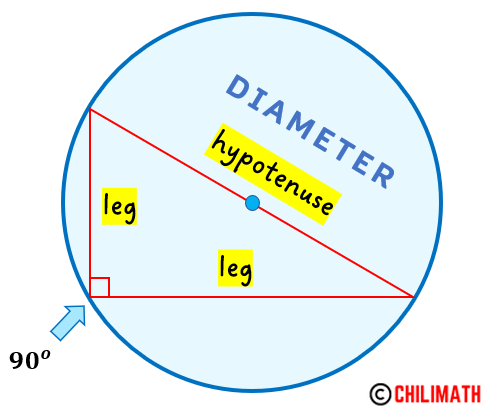
Here’s the Pythagorean Theorem in a nutshell.
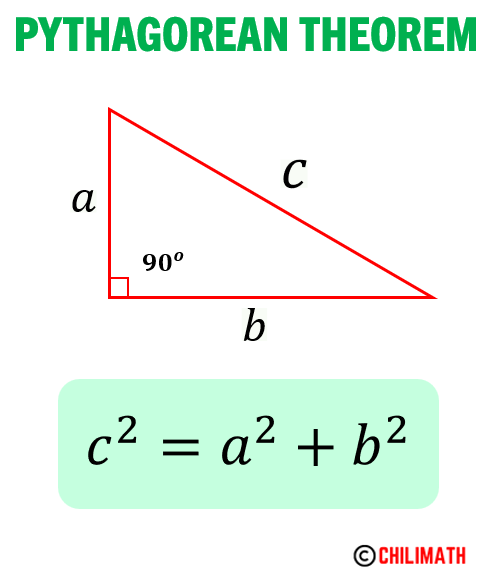
In a right triangle, the square of the length of the hypotenuse [latex]c[/latex] (longest side, side opposite the 90-degree angle) is equal to the sum of the squares of the lengths of the legs, namely [latex]a[/latex] and [latex]b[/latex].
At this point, we should have all of the necessary information to solve this problem. Let’s use the Pythagorean Theorem to find the hypotenuse. In this case, the hypotenuse is the diameter of the circle. So, once we’ve determined the hypotenuse, we’ll use its value to calculate the circumference of the circle.
Let’s calculate now the length of the hypotenuse [latex]c[/latex] which at the same time the diameter of the circle.
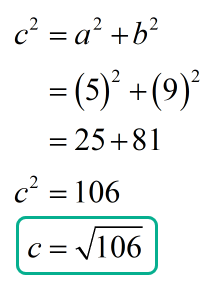
After finding the diameter of the circle, it is finally time to solve for the circumference of the circle.
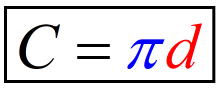
Make sure that you use the prescribed value of [latex]\pi[/latex] in this problem which is [latex]\pi = {{22} \over 7}[/latex]. Also, don’t round intermediate calculations.
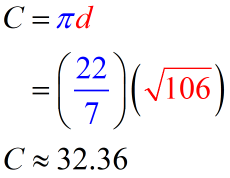
Therefore, the circumference of the circle is [latex]32.36[/latex].
Example 7: The two circles below are concentric. The radius of the inner circle is [latex]14[/latex] inches while the radius of the outer circle is [latex]23[/latex] inches. How much longer is the circumference of the outer circle than the inner circle?
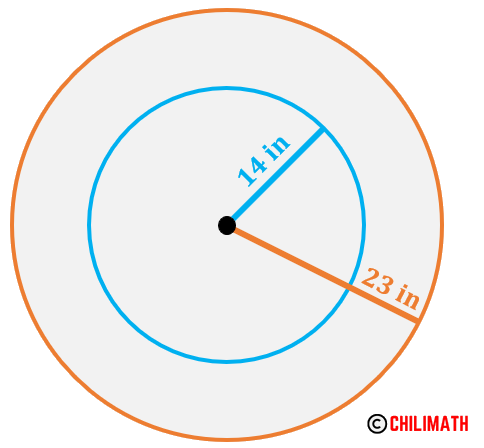
We’re working with two circles here: an inner circle and an outer circle. Because both of their radii are given, we can easily calculate their circumference. We know that a circumference is just the length of the distance around the circle. Thus, their lengths can be compared, i.e. how much longer one is than the other. That is exactly what this problem requires of us.
So our plan is to determine the circumferences of the inner and outer circles. Then, we subtract the circumference of the inner circle from the circumference of the outer circle to get our desired answer.
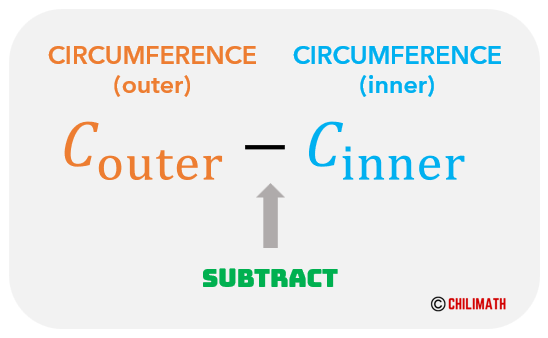
Here are the calculations of the circumferences of the outer and inner circles:

Let’s subtract the circumference of the inner from the outer’s to get our final answer.
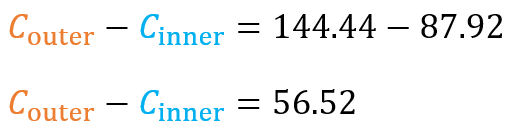
Therefore, the final answer is [latex]56.52[/latex].
Example 8: Find the circumference of the smaller (inner) circle given that the circles are concentric.

Our goal here is to determine the circumference of the smaller circle. Right now, we don’t know the radius of the smaller circle. But believe me, we do have enough information to find it.
Let’s focus our attention first on the larger (outer) circle. Since the circumference is provided, we should be able to find its radius. If you closely examine the diagram, the radius of the larger circle is equal to the radius of the smaller circle plus [latex]6[/latex]. Do you see why?
Take a look at the diagram below.
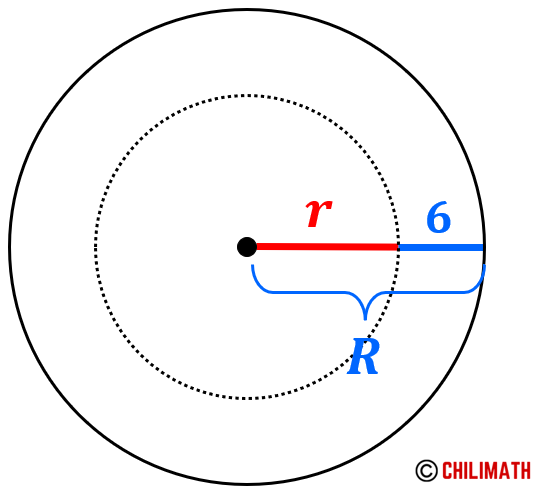
That means the radius of the larger circle is the little [latex]r[/latex] plus [latex]6[/latex].
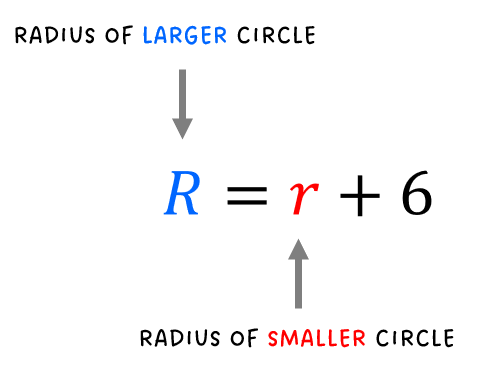
So that means if we can find the radius of the larger circle, we can subtract it by [latex]6[/latex] to obtain the radius of the smaller circle. Finally, use the radius of the smaller circle to find the circumference of the smaller circle.
Calculating the radius of the larger circle:
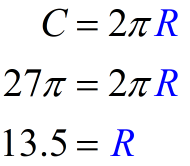
Calculating the radius of the smaller circle:
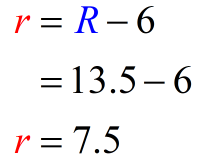
Finally, we can compute the circumference of the smaller (inner) circle as required by the problem.
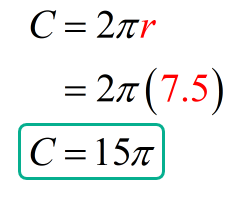
Therefore, the circumference of the smaller or inner circle is [latex]15\pi [/latex].
You may also be interested in these related math lessons or tutorials:
