Prove: The Sum of Two Odd Numbers is an Even Number
We want to show that if we add two odd numbers, the sum is always an even number.
Before we even write the actual proof, we need to convince ourselves that the given statement has some truth to it. We can test the statement with a few examples.
I prepared the table below to gather the results of some of the numbers that I used to test the statement.
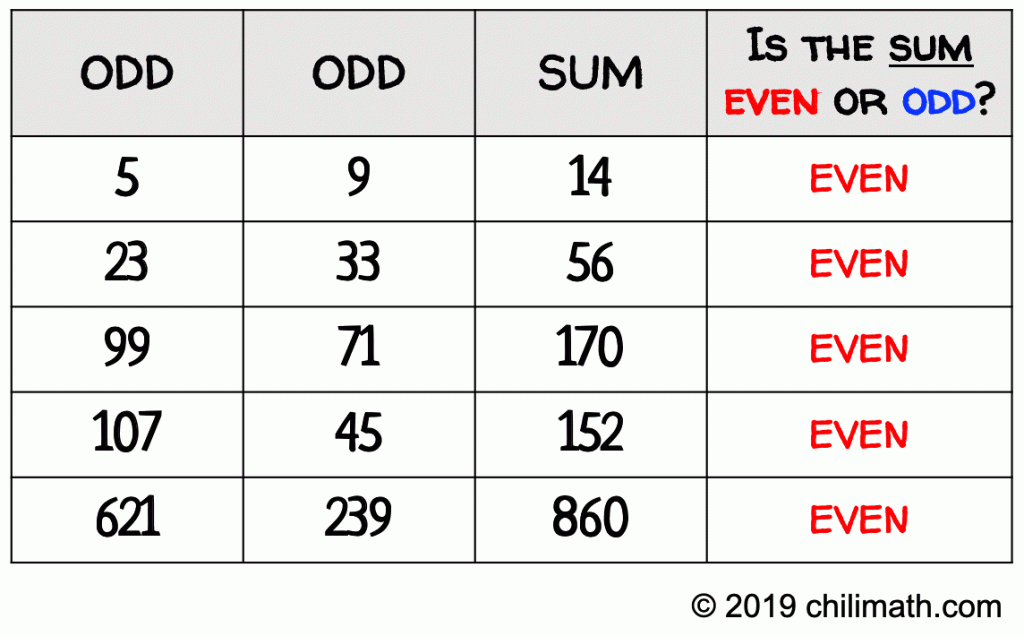
It appears that the statement, the sum of two odd numbers is even, is true. However, by simply providing infinitely many examples do not constitute proof. It is impossible to list all possible cases.
Instead, we need to show that the statement holds true for ALL possible cases. The only way to achieve that is to express an odd number in its general form. Then, we add the two odd numbers written in general form to get a sum of an even number expressed in a general form as well.
To write the proof of this theorem, you should already have a clear understanding of the general forms of both even and odd numbers.
The number [latex]n[/latex] is even if it can be expressed as
[latex]n=2k[/latex]
where [latex]k[/latex] is an integer.
On the other hand, the number [latex]n[/latex] is odd if it can be written as
[latex]n=2k+1[/latex]
such that [latex]k[/latex] is some integer.
BRAINSTORM BEFORE WRITING THE PROOF

Note: The purpose of brainstorming in writing proof is for us to understand what the theorem is trying to convey; and gather enough information to connect the dots, which will be used to bridge the hypothesis and the conclusion.
Let’s take two arbitrary odd numbers [latex]2a + 1[/latex] and [latex]2b + 1[/latex] where [latex]a[/latex] and [latex]b[/latex] are integers.
Since we are after the sum, we want to add [latex]2a + 1[/latex] and [latex]2b + 1[/latex].
[latex]\left( {2a + 1} \right) + \left( {2b + 1} \right)[/latex]
which gives us
[latex]\left( {2a + 1} \right) + \left( {2b + 1} \right) = 2a + 2b + 2[/latex].
Notice that we can’t combine [latex]2a[/latex] and [latex]2b[/latex] because they are not similar terms. However, we are successful in combining the constants, thus [latex]1 + 1 = 2[/latex].
What can we do next? If you think about it, there is a common factor of [latex]2[/latex] in [latex]2a + 2b + 2[/latex]. If we factor out the [latex]2[/latex], we obtain [latex]2\left( {a + b + 1} \right)[/latex].
What’s next? Well, if we look inside the parenthesis, it’s obvious that what we have is just an integer. It may not appear as an integer at first because we see a bunch of integers being added together.
Recall the Closure Property of Addition for the set of integers.
Suppose [latex]a[/latex] and [latex]b[/latex] belong to the set of integers. The sum of [latex]a[/latex] and [latex]b[/latex] which is [latex]{a+b}[/latex] is also an integer.
In fact, you can expand this closure property of addition to more than two integers. For example, the sum of the integers [latex]-7[/latex], [latex]-1[/latex], [latex]0[/latex], [latex]4[/latex], and [latex]10[/latex] is [latex]6[/latex] which is also an integer. Thus,
[latex](-7)+(-1)+0+4+10=6[/latex].
Going back to where we left off, in [latex]2\left( {a + b + 1} \right)[/latex], the expression inside the parenthesis is just an integer since the sum of the integers [latex]a[/latex], [latex]b[/latex] and [latex]1[/latex] is just another integer. For simplicity’s sake, let’s call it integer [latex]k[/latex].
So then,
[latex]a+b+1=k[/latex]
That means [latex]2\left( {a + b + 1} \right)[/latex] can be expressed as
[latex]2\left( {a + b + 1} \right) =2k[/latex]
where [latex]2k[/latex] is the general form of an even number. It looks like we have successfully achieved what we want to show that the sum of two odds is even.
WRITE THE PROOF
THEOREM: The sum of two odd numbers is an even number.
PROOF: Suppose [latex]2a+1[/latex] and [latex]2b+1[/latex] are any two odd numbers where [latex]a[/latex] and [latex]b[/latex] are integers. The sum of these two odd numbers is [latex]\left( {2a + 1} \right) + \left( {2b + 1} \right)[/latex]. This can be simplified as [latex]{2a + 2b + 2}[/latex] by combining similar terms. Factor out the greatest common factor (GCF) of [latex]\bold{2}[/latex] from [latex]{2a+2b+2}[/latex] to get [latex]2\left( {a + b + 1} \right)[/latex]. Since the sum of integers is just another integer, say integer [latex]k[/latex], then [latex]{k=a+b+1}[/latex]. By substitution, we have [latex]2\left( {a + b + 1} \right) = 2k[/latex] where [latex]2k[/latex] is clearly the general form of an even number. Therefore, the sum of two odd numbers is an even number. ◾️
You may also be interested in these related math lessons or tutorials:
