Prove: The Sum of Two Even Numbers is an Even Number
It looks obvious that the sum of two even numbers is always an even number. We can provide a few examples to demonstrate the possibility that the statement is indeed true.
See the table below.
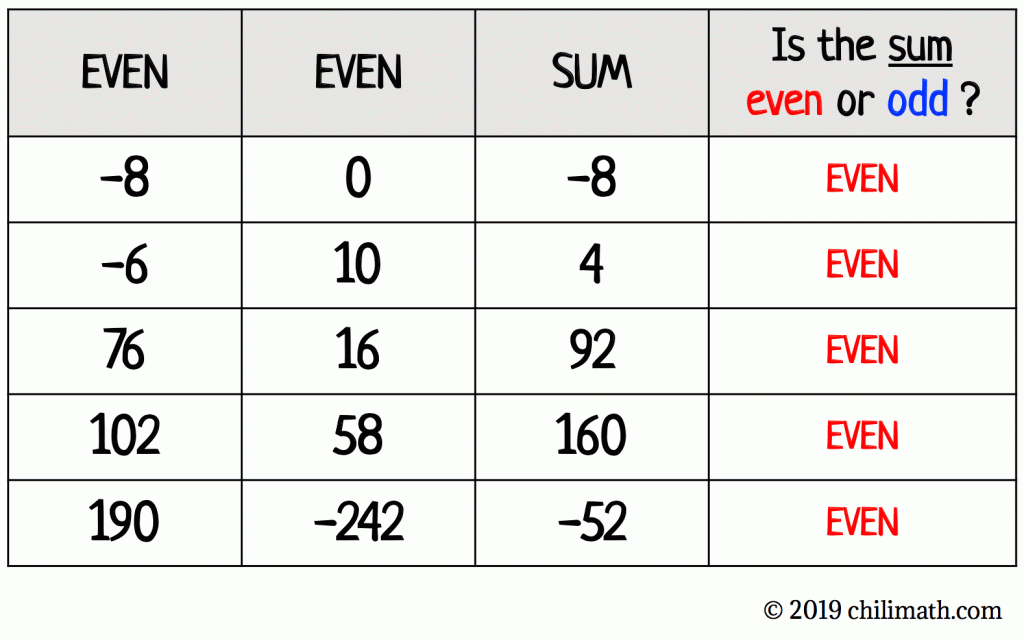
We know that simply giving examples is not proof. So let’s start formulating our proof.
BRAINSTORM BEFORE WRITING THE PROOF

Note: The purpose of brainstorming in writing proof is for us to understand what the theorem is trying to convey; and gather enough information to connect the dots, which will be used to bridge the hypothesis and the conclusion.
At the back of our head, we should know what an even number looks like. The general form of an even number is shown below.

Meaning, [latex]\textbf{m}[/latex] is an even number if it can be expressed as
[latex]\textbf{m}=\textbf{2r}[/latex] where [latex]\textbf{r}[/latex] is just another integer.
Below are examples of even numbers because they can all be written as a product of [latex]2[/latex] and an integer [latex]r[/latex].
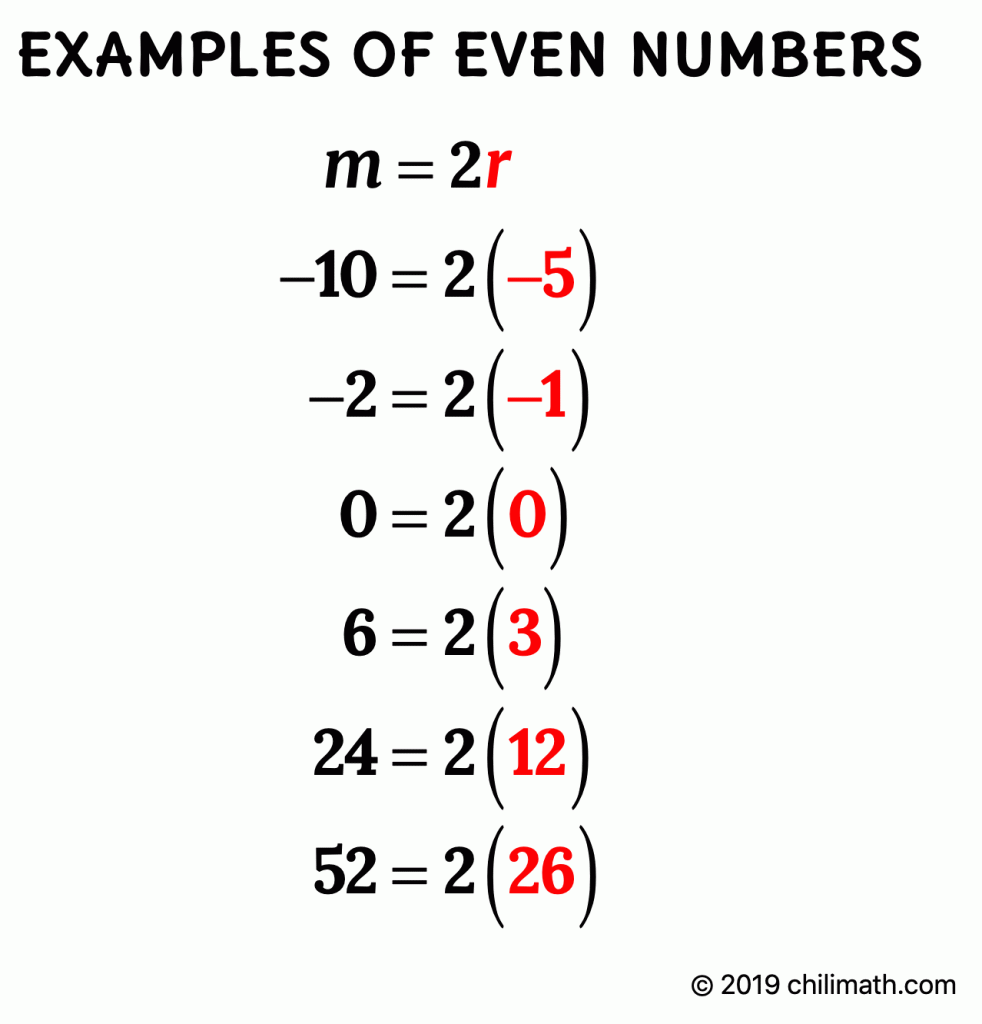
After having a good intuitive understanding of what an even number is, we are ready to move to the next step. Suppose we pick any two even numbers. Let’s call them
[latex]2r[/latex] and [latex]2s[/latex].
Let’s sum it up.
[latex]2r + 2s[/latex]
We can’t combine them into a single algebraic expression because they have different variables. However, factoring out the number [latex]2[/latex] is the obvious next step.
[latex]2r + 2s = 2\left( {r + s} \right)[/latex]
It should be very clear at this point that [latex]\textbf{2(r + s)}[/latex] must also be an even number since the sum of the integers [latex]r[/latex] and [latex]s[/latex] is just another integer.
If we let [latex]n[/latex] be the sum of integers [latex]r[/latex] and [latex]s[/latex], then [latex]n = r + s[/latex]. Therefore, we can rewrite [latex]2(r + s)[/latex] as [latex]\textbf{2n}[/latex] which is without a doubt an even number.
WRITE THE PROOF
THEOREM: The sum of two even numbers is an even number.
PROOF: Start by picking any two integers. We can write them as [latex]2x[/latex] and [latex]2y[/latex]. The sum of these two even numbers is [latex]2x + 2y[/latex]. Now, factor out the common factor [latex]2[/latex]. That means [latex]2x + 2y[/latex] = [latex]2(x + y)[/latex]. Inside the parenthesis, we have a sum of two integers. Since the sum of two integers is just another integer then we can let integer [latex]n[/latex] be equal to [latex](x + y)[/latex]. Substituting [latex](x + y)[/latex] by [latex]n[/latex] in [latex]2(x + y)[/latex], we obtain [latex]\textbf{2n}[/latex] which is clearly an even number. Thus, the sum of two even numbers is even.◾️
You may also be interested in these related math lessons or tutorials:
