Algebraic Expressions
Math, like any other language, has a way of communicating ideas. An algebraic expression is a concise way of describing mathematical objects through the use of numbers, variables (letters), and arithmetic operations such as addition, subtraction, multiplication, and division.
The three main components of algebraic expressions are numbers, variables, and arithmetic operations.
- Numbers or Constants
Examples: [latex]1[/latex], [latex]6[/latex], [latex]8[/latex], [latex]27[/latex], [latex]32[/latex], etc.
- Variables or Letters
Examples: [latex]x[/latex], [latex]y[/latex], [latex]a[/latex], [latex]h[/latex], [latex]p[/latex], etc.
- Arithmetic Operations
Examples: [latex]+[/latex] (addition), [latex] – [/latex] (subtraction) , [latex] \times[/latex] (multiplication) , [latex]÷[/latex] (division)
The following are easy examples that can help you get familiar with the operations of addition, subtraction, multiplication, and division.
- Addition
the sum of [latex]x[/latex] and [latex]5[/latex] → [latex]x+5[/latex]
- Subtraction
the difference of [latex]y[/latex] and [latex]3[/latex] → [latex]y-3[/latex]
- Multiplication
the product of [latex]n[/latex] and [latex]2[/latex] → [latex]2n[/latex]
- Division
the quotient of [latex]k[/latex] and [latex]7[/latex] → [latex]\Large{{k \over 7}}[/latex]
Writing Algebraic Expressions Step-by-Step Examples
Let’s go over more examples.
Example 1: The sum of twice a number and [latex]3[/latex]
Answer: Let variable [latex]x[/latex] be the unknown number. So twice a number means [latex]2x[/latex]. The sum (use plus symbol) of twice a number and [latex]3[/latex] can be written as [latex]2x+3[/latex].
Example 2: The difference of triple a number and [latex]5[/latex]
Answer: Let variable [latex]y[/latex] be the unknown number. So triple a number means [latex]3y[/latex]. The difference (use minus symbol) of triple a number and [latex]5[/latex] should be written as [latex]3y – 5[/latex].
Example 3: The sum of the quotient of [latex]m[/latex] and [latex]2[/latex], and the product of [latex]4[/latex] and [latex]n[/latex].
Answer: In this case, the unknown numbers are already provided as [latex]m[/latex] and [latex]n[/latex]. That’s one less thing to worry about.
The key is to recognize that we are going to add a quotient and a product.
- the quotient of [latex]m[/latex] and [latex]2[/latex] is expressed as [latex]\Large{{m \over 2}}[/latex]
- the product of [latex]4[/latex] and [latex]n[/latex] is expressed as [latex]4n[/latex]
Therefore, the sum of the quotient and product is [latex]{\Large{{m \over 2}}} + 4n[/latex].
Example 4: The difference of the product of [latex]7[/latex] and [latex]w[/latex], and the quotient of [latex]2[/latex] and [latex]v[/latex].
Answer: In this case, the unknown numbers have been assigned with corresponding variables which are [latex]w[/latex] and [latex]v[/latex].
The key is to recognize that we are going to subtract the product by the quotient of some expressions.
- the product of [latex]7[/latex] and [latex]w[/latex] is expressed as [latex]7w[/latex]
- the quotient of [latex]2[/latex] and [latex]v[/latex] is expressed as [latex]\Large{{2 \over v}}[/latex]
Therefore, the difference of the product and quotient is [latex]7w – {\Large{{2 \over v}}}[/latex].
Common Words or Terms to Mean Addition, Subtraction, Multiplication, and Division
Let’s go over some common words or phrases that describe the four arithmetic operations. It is critical that you understand these words or phrases in order to successfully write or interpret any given algebraic expression.


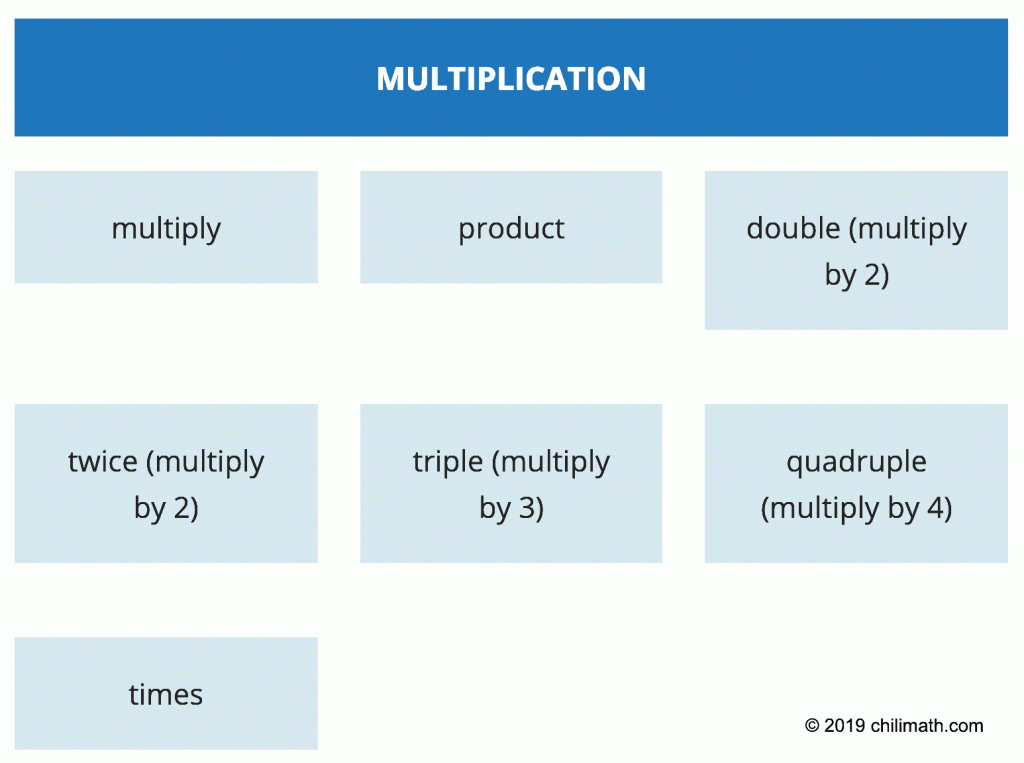
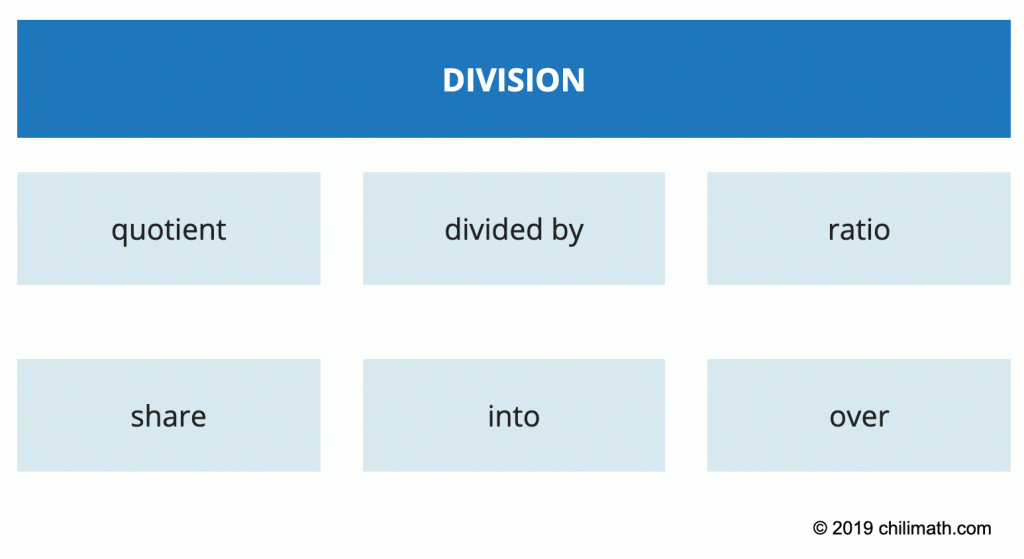
Math Phrases into Algebraic Expressions
The key to learning is to study a LOT of examples!
| MATH PHRASES | ALGEBRAIC EXPRESSIONS |
|---|---|
| a number plus 9 | y + 9 |
| the sum of a number and 10 | m + 10 |
| total of a number and 5 | b + 5 |
| a number increased by 4 | x + 4 |
| h take away 2 | h − 2 |
| 2 take away by a number | 2 − h |
| a number minus 11 | k − 11 |
| 11 minus a number | 11 − k |
| a number decreased by 7 | y − 7 |
| the difference of n and 25 | n − 25 |
| the difference of 25 and n | 25 − n |
| 5 less than a number | x − 5 |
| x less than the number 5 | 5 − x |
| the product of r and 4 | 4r |
| 7 times a number | 7p |
| double a number | 2x |
| triple a number | 3x |
| a number divided by 4 | w / 4 |
| the quotient of w and 6 | w / 6 |
| the quotient of 12 and m | 12 / m |
| a number divided by 3 | f / 3 |
| t over 7 | t / 7 |
| 5 into a number | a / 5 |
| a number into 5 | 5 / a |
| the sum of x and 7 divided by 2 | ( x + 7 ) / 2 |
| the difference of m and 3 over 5 | ( m − 3) / 5 |
| 11 more than the product of 3 and y | 3y + 11 |
| 6 less than the quotient of c and 10 | ( c / 10 ) − 6 |
| 3 minus the product of 5 and a number | 3 − 5x |
| the sum of 5 and the quotient of z and 7 | ( z / 7 ) + 5 |
| the difference of twice a number and 3 | 2m − 3 |
You may also be interested in these related math lessons or tutorials:
