Solving Rational Equations
A rational equation is a type of equation where it involves at least one rational expression, a fancy name for a fraction. The best approach to address this type of equation is to eliminate all the denominators using the idea of LCD (least common denominator). By doing so, the leftover equation to deal with is usually either linear or quadratic.
In this lesson, I want to go over ten (10) worked examples with various levels of difficulty. I believe that most of us learn math by looking at many examples. Here we go!
Examples of How to Solve Rational Equations
Example 1: Solve the rational equation below and make sure you check your answers for extraneous values.
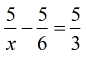
Would it be nice if the denominators are not there? Well, we can’t simply vanish them without any valid algebraic step. The approach is to find the Least Common Denominator (also known Least Common Multiple) and use that to multiply both sides of the rational equation. It results in the removal of the denominators, leaving us with regular equations that we already know how to solve such as linear and quadratic. That is the essence of solving rational equations.
- The LCD is [latex]6x[/latex]. I will multiply both sides of the rational equation by [latex]6x[/latex] to eliminate the denominators. That’s our goal anyway – to make our life much easier.
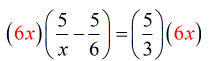
- You should have something like this after distributing the LCD.
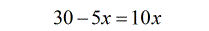
- I decided to keep the variable [latex]x[/latex] on the right side. So remove the [latex]-5x[/latex] on the left by adding both sides by [latex]5x[/latex].
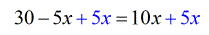
- Simplify. It’s obvious now how to solve this one-step equation. Divide both sides by the coefficient of [latex]5x[/latex].
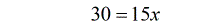
- Yep! The final answer is [latex]x = 2[/latex] after checking it back into the original rational equation. It yields a true statement.
Always check your “solved answers” back into the original equation to exclude extraneous solutions. This is a critical aspect of the overall approach when dealing with problems like Rational Equations and Radical Equations.
Example 2: Solve the rational equation below and make sure you check your answers for extraneous values.
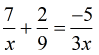
The first step in solving a rational equation is always to find the “silver bullet” known as LCD. So for this problem, finding the LCD is simple.
Here we go.
Try to express each denominator as unique powers of prime numbers, variables and/or terms.
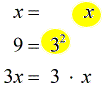
Multiply together the ones with the highest exponents for each unique prime number, variable and/or terms to get the required LCD.
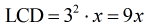
- The LCD is [latex]9x[/latex]. Distribute it to both sides of the equation to eliminate the denominators.
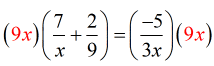
- Simplify.
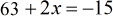
- To keep the variables on the left side, subtract both sides by [latex]63[/latex].
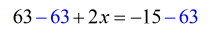
- The resulting equation is just a one-step equation. Divide both sides by the coefficient of [latex]x[/latex].
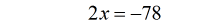
- That is it! Check the value [latex]x = – \,39[/latex] back into the main rational equation and it should convince you that it works.
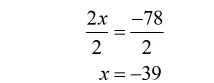
Example 3: Solve the rational equation below and make sure you check your answers for extraneous values.
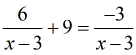
It looks like the LCD is already given. We have a unique and common term [latex]\left( {x – 3} \right)[/latex] for both of the denominators. The number [latex]9[/latex] has the trivial denominator of [latex]1[/latex] so I will disregard it. Therefore the LCD must be [latex]\left( {x – 3} \right)[/latex].
- The LCD here is [latex]\left( {x – 3} \right)[/latex]. Use it as a multiplier to both sides of the rational equation.
](https://www.chilimath.com/wp-content/uploads/2017/07/ex3_steps_r1_c1.gif)
- I hope you get this linear equation after performing some cancellations.
Distribute the constant [latex]9[/latex] into [latex]\left( {x – 3} \right)[/latex].
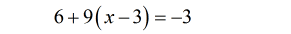
- Combine the constants on the left side of the equation.
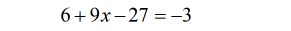
- Simplify
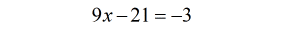
- Move all the numbers to the right side by adding [latex]21[/latex] to both sides.
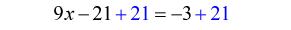
- Simplify
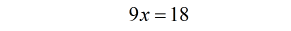
- Not too bad. Again make it a habit to check the solved “answer” from the original equation.
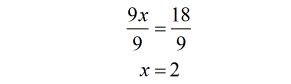
It should work so yes, [latex]x = 2[/latex] is the final answer.
Example 4: Solve the rational equation below and make sure you check your answers for extraneous values.
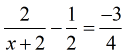
I hope that you can tell now what’s the LCD for this problem by inspection. If not, you’ll be fine. Just keep going over a few examples and it will make more sense as you go along.
Try to express each denominator as unique powers of prime numbers, variables and/or terms.
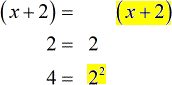
Multiply together the ones with the highest exponents for each unique prime number, variable and/or terms to get the required LCD.
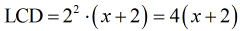
- The LCD is [latex]4\left( {x + 2} \right)[/latex]. Multiply each side of the equations by it.
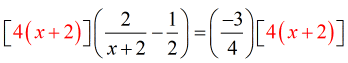
- After careful distribution of the LCD into the rational equation, I hope you have this linear equation as well.
Quick note: If ever you’re faced with leftovers in the denominator after multiplication, that means you have an incorrect LCD.
Now, distribute the constants into the parenthesis on both sides.
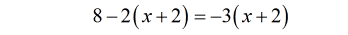
- Combine the constants on the left side to simplify it.
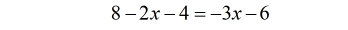
- At this point, make the decision where to keep the variable.
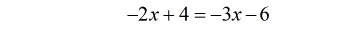
- Keeping the [latex]x[/latex] to the left means we subtract both sides by [latex]4[/latex].

- Simplify
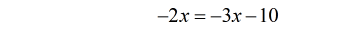
- Add both sides by [latex]3x[/latex].
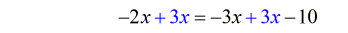
- That’s it. Check your answer to verify its validity.
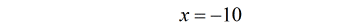
Example 5: Solve the rational equation below and make sure you check your answers for extraneous values.
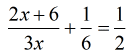
Focusing on the denominators, the LCD should be [latex]6x[/latex]. Why?
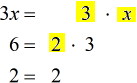
Remember, multiply together “each copy” of the prime numbers or variables with the highest powers.
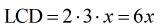
- The LCD is [latex]6x[/latex]. Distribute to both sides of the given rational equation.
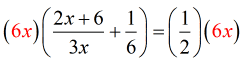
- It should look like after careful cancellation of similar terms.
Distribute the constant into the parenthesis.
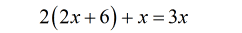
- The variable [latex]x[/latex] can be combined on the left side of the equation.
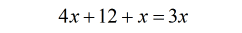
- Since there’s only one constant on the left, I will keep the variable [latex]x[/latex] to the opposite side.
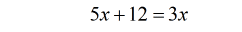
- So I subtract both sides by [latex]5x[/latex].
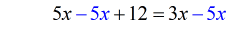
- Divide both sides by [latex]-2[/latex] to isolate [latex]x[/latex].
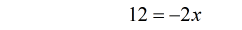
- Yep! We got the final answer.
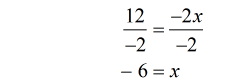
Example 6: Solve the rational equation below and make sure you check your answers for extraneous values.
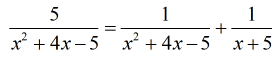
Whenever you see a trinomial in the denominator, always factor it out to identify the unique terms. By simple factorization, I found that [latex]{x^2} + 4x – 5 = \left( {x + 5} \right)\left( {x – 1} \right)[/latex]. Not too bad?
Finding the LCD just like in previous problems.
Try to express each denominator as unique powers of prime numbers, variables and/or terms. In this case, we have terms in the form of binomials.
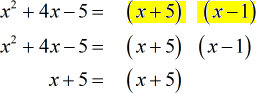
Multiply together the ones with the highest exponents for each unique copy of a prime number, variable and/or terms to get the required LCD.
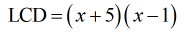
- Before I distribute the LCD into the rational equations, factor out the denominators completely.
This aids in the cancellations of the commons terms later.
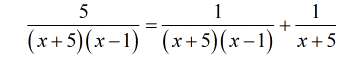
- Multiply each side by the LCD.
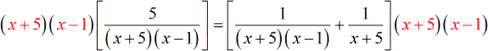
- Wow! It’s amazing how quickly the “clutter” of the original problem has been cleaned up.
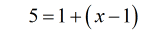
- Get rid of the parenthesis by the distributive property.
You should end up with a very simple equation to solve.
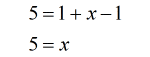
Example 7: Solve the rational equation below and make sure you check your answers for extraneous values.
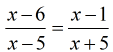
Since the denominators are two unique binomials, it makes sense that the LCD is just their product.
- The LCD is [latex]\left( {x + 5} \right)\left( {x – 5} \right)[/latex]. Distribute this into the rational equation.
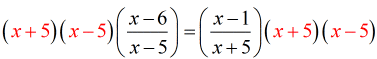
- It results in a product of two binomials on both sides of the equation.
It makes a lot of sense to perform the FOIL method. Does that ring a bell?
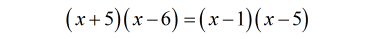
- I expanded both sides of the equation using FOIL. You should have a similar setup up to this point. Now combine like terms (the [latex]x[/latex]) in both sides of the equation.
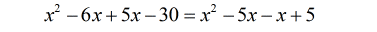
- What’s wonderful about this is that the squared terms are exactly the same! They should cancel each other out. We could have bumped into a problem if their signs are opposite.
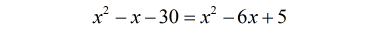
- Subtract both sides by [latex]{x^2}[/latex].
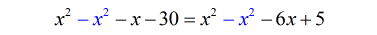
- The problem is reduced to a regular linear equation from a quadratic.
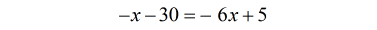
- To isolate the variable [latex]x[/latex] on the left side implies adding both sides by [latex]6x[/latex].
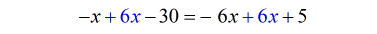
- Move all constant to the right.
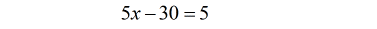
- Add both sides by [latex]30[/latex].
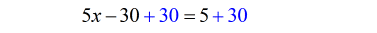
- Finally, divide both sides by [latex]5[/latex] and we are done.
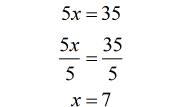
Example 8: Solve the rational equation below and make sure you check your answers for extraneous values.
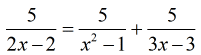
This one looks a bit intimidating. But if we stick to the basics, like finding the LCD correctly, and multiplying it across the equation carefully, we should realize that we can control this “beast” quite easily.
Expressing each denominator as unique powers of terms
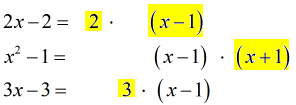
Multiply each unique terms with the highest power to obtain the LCD

- Factor out the denominators.
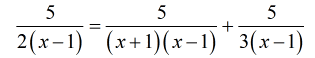
- Multiply both sides by the LCD obtained above.
Be careful now with your cancellations.
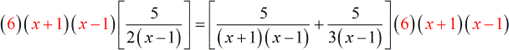
- You should end up with something like this when done right.
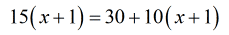
- Next step, distribute the constants into the parenthesis.
This is getting simpler in each step!
I would combine like terms on both sides also to simplify further.
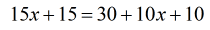
- This is just a multi-step equation with variables on both sides. Easy!
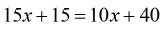
- To keep [latex]x[/latex] on the left side, subtract both sides by [latex]10x[/latex].
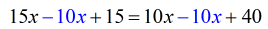
- Move all the pure numbers to the right side.
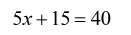
- Subtract both sides by [latex]15[/latex].
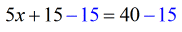
- A simple one-step equation.
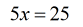
- Divide both sides by [latex]5[/latex] to get the final answer. Again, don’t forget to check the value back into the original equation to verify.
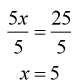
Example 9: Solve the rational equation below and make sure you check your answers for extraneous values.
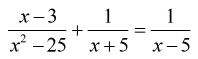
Let’s find the LCD for this problem, and use it to get rid of all the denominators.
Express each denominator as unique powers of terms.
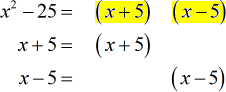
Multiply each unique term with the highest power to determine the LCD.
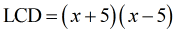
- Factor out the denominators completely
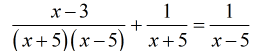
- Distribute the LCD found above into the given rational equation to eliminate all the denominators.
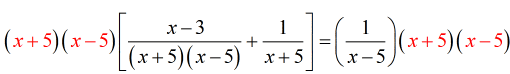
- We reduced the problem into a very easy linear equation. That’s the “magic” of using LCD.
Multiply the constants into the parenthesis.
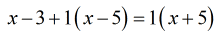
- Combine similar terms
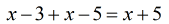
- Simplify
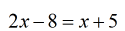
- Keep the variable to the left side by subtracting [latex]x[/latex] on both sides.
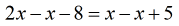
- Keep constants to the right.
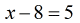
- Add both sides by [latex]8[/latex] to solve for [latex]x[/latex]. Done!
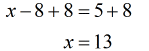
Example 10: Solve the rational equation below and make sure you check your answers for extraneous values.
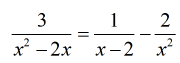
Start by determining the LCD. Express each denominator as powers of unique terms. Then multiply together the expressions with the highest exponents for each unique term to get the required LCD.
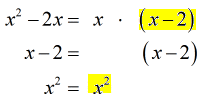
So then we have,
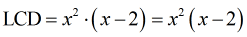
- Factor out the denominators completely.
![3/[x(x-2)] = - 2/x^2](https://www.chilimath.com/wp-content/uploads/2017/07/ex10_steps_r2_c2.gif)
- Distribute the LCD found above into the rational equation to eliminate all the denominators.
![(x^2)(x-2){3/[x(x-2)]} = { - }(x^2)(x-2)](https://www.chilimath.com/wp-content/uploads/2017/07/ex10_steps_r3_c1.gif)
- Distribute the constant into the parenthesis.
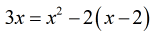
- Critical Step: We are dealing with a quadratic equation here. Therefore keep everything (both variables and constants) on one side forcing the opposite side to equal zero.
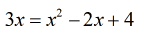
- I can make the left side equal to zero by subtracting both sides by [latex]3x[/latex].
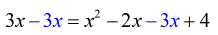
- At this point, it is clear that we have a quadratic equation to solve.
Always start with the simplest method before trying anything else. I will utilize the factoring method of the form [latex]x^2+bx+c=0[/latex] since the trinomial is easily factorable by inspection.
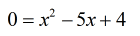
- The factors of [latex]{x^2} – 5x + 4 = \left( {x – 1} \right)\left( {x – 4} \right)[/latex]. You can check it by the FOIL method.
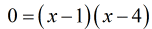
- Use the Zero Product Property to solve for [latex]x[/latex].
Set each factor equal to zero, then solve each simple one-step equation.
Again, always check the solved answers back into the original equations to make sure they are valid.
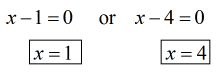
You may also be interested in these related math lessons or tutorials:
Adding and Subtracting Rational Expressions
