Adding and Subtracting Rational Expressions
If you know how to add or subtract fractions with the same or different denominators, adding and subtracting rational expressions should be easy for you. The procedures between the two are very similar.
Let’s review by going over two examples: one with the same denominator, and another with different denominators.
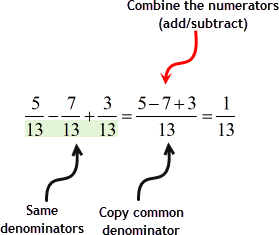
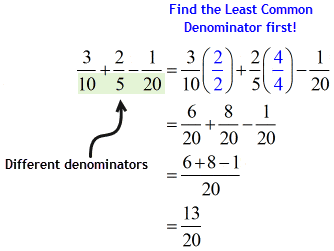
Steps on How to Add and Subtract Rational Expressions
1) Make the denominators of the rational expressions the same by finding the Least Common Denominator (LCD).
Note: The Least Common Denominator is the same as the Least Common Multiple (LCM) of the given denominators.
2) Next, combine the numerators by the indicated operations (add and/or subtract) then copy the common denominator.
Note: Don’t forget to simplify further the rational expression by canceling common factors, if possible.
As they say, practice makes perfect. So we will go over six (6) worked examples in this lesson to illustrate how it is being done. Let’s get started!
Examples of Adding and Subtracting Rational Expressions
Example 1: Add and subtract the rational expressions below.
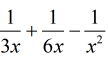
In this case, we are adding and subtracting rational expressions with unlike denominators. Our goal is to make them all the same.
Since I have monomials in the denominators, the LCD can be obtained by simply taking the Least Common Multiple of the coefficients, where LCM ([latex]3[/latex],[latex]6[/latex]) = [latex]6[/latex], and multiply that to the variable [latex]x[/latex] with the highest exponent.
The LCD should be (LCM of coefficients) times (LCM of variable [latex]x[/latex]) which gives us [latex]\left( 6 \right)\left( {{x^2}} \right) = 6{x^2}[/latex].
- The LCD is [latex]6{x^2}[/latex] thus I need to somehow convert all the denominators to that.
The “blue fractions” are the appropriate multipliers to do the job!
![= [(1/3x)(2x/2x)]+[(1/6x)(x/x)]-[(1/x^2)(6/6)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex1_r1_c2.gif)
- After simplifying the fractions by multiplication, you should have this setup.
Now that we have the same denominators, it is easy to simplify.
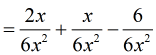
- I will copy the common denominator and perform the indicated operations on the numerators.
Combine similar terms (see the [latex]x[/latex] variables?).
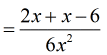
- When you reach the point of having a single rational expression, your next critical step is to factor the top and the bottom completely.
The reason is that you may have common factors, which can be canceled out.
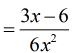
- I factor out the number [latex]3[/latex] from the numerator.
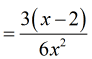
- [latex]3[/latex] can go into [latex]6[/latex] by [latex]2[/latex].
![=[3(x-2)]/6x^2](https://www.chilimath.com/wp-content/uploads/2017/07/ex1_r5_c2_cancelled.gif)
To make this a better answer, I will exclude the value of [latex]x[/latex] that can make the original rational expression undefined.
I can add the condition that [latex]x \ne 0[/latex].
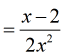
Example 2: Add the rational expressions below.
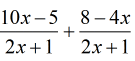
This problem contains like denominators. We want this because it is the LCD itself – the given denominator of the rational expression.
So then the LCD that we are going to use is [latex]2x + 1[/latex].
- Simplify by copying the common denominator then adding the numerators.
Tip: Don’t rush by immediately doing all the calculations in your head. I suggest that you place each term inside the parenthesis before performing the required operation. This extra step may be your lifesaver to avoid careless mistakes.
![=[(10x-5)+(8-4x)]/(2x+1)](https://www.chilimath.com/wp-content/uploads/2017/07/ex2_r1_c2.gif)
- Unless you have a good grasp on how to effectively combine like terms, I suggest you take another “baby step” as an additional precaution.
Do you see how I decided to place the like terms side-by-side on the numerator?
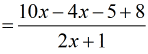
- After combining like terms, you should have something similar to this.
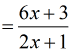
- Next, factor out [latex]3[/latex] from the top.
![=[3(2x+1]/(2x+1)](https://www.chilimath.com/wp-content/uploads/2017/07/ex2_r4_c2.gif)
- This is great because we have common factors to cancel.
![=[3(2x+1)]/(2x+1)](https://www.chilimath.com/wp-content/uploads/2017/07/ex2_r5_c2.gif)
- Get rid of them by cancellation.
![=[3(2x+1)]/(2x+1)](https://www.chilimath.com/wp-content/uploads/2017/07/ex2_r5_c2_cancelled.gif)
- That’s right! When it’s simplified the answer is just [latex]3[/latex].
To prevent the original rational expression to have a denominator of zero, we say that [latex]x \ne – {1 \over 2}[/latex].
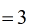
Example 3: Add the rational expressions below.
![[(x+6)/(x^2-x-20)]+[(2x-21)/(x^2-x-20)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex3_r1_c1.gif)
This time I have the same trinomial in both denominators. This is similar to problem #2 but the quadratic trinomial adds a layer of fun. Later, I can factor out the denominator to see if there are common factors to cancel against the numerator.
- Copy the common denominator and set it up just like this – placing each numerator in the parenthesis before adding them.
![=[(x+6)+(2x-21)]/(x^2-x-20)](https://www.chilimath.com/wp-content/uploads/2017/07/ex3_r1_c2.gif)
- Rearrange the terms in such a way that similar terms are next to each other for ease of computation later.
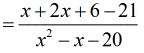
- This is what I got after combining the variables and constants together.
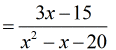
- Factor out the numerator.
![=[3(x-5)]/(x^2-x-20)](https://www.chilimath.com/wp-content/uploads/2017/07/ex3_r4_c2.gif)
- Factor out the denominator.
![=[3(x-5)]/[(x-5)(x+4)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex3_r5_c2.gif)
- I see that [latex]\left( {x – 5} \right)[/latex] is a common factor so I cancel it.
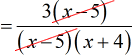
- This is the leftover and should be our final answer.
You may say that [latex]x \ne – \,4[/latex] and [latex]x \ne + \,5[/latex] from the original denominator.
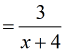
Example 4: Subtract the rational expressions below.
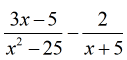
This is a good example because the denominators are different. I need to find the LCD by doing the following steps.
Factor each denominator completely, and line up the common factors. Identify each unique factor with the highest power.
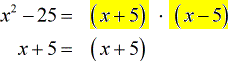
Multiply together the ones with the highest exponents for each unique factor.
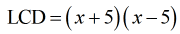
- In this step, I haven’t done anything but factor out the denominator of the first rational expression.
![=[(3x-5)/(x+5)(x-5)]-[2/(x+5)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex4_r1_c2.gif)
- Use our LCD = [latex]\left( {x + 5} \right)\left( {x – 5} \right)[/latex] as guide to make the denominators equal.
The first denominator is okay but the second one is lacking [latex]\left( {x – 5} \right)[/latex].
This is why I multiply it by the blue fraction.
![=[(3x-5)/(x+5)(x-5)]-[2/(x+5)][(x-5)/(x-5)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex4_r3_c2.gif)
- Simplify the second rational expression by multiplication.
![= [(3x-5)/(x+5)(x-5)]-{[2(x-5)]/[(x+5)(x-5)]}](https://www.chilimath.com/wp-content/uploads/2017/07/ex4_r4_c2.gif)
- Here, I distributed the [latex]2[/latex] into [latex]\left( {x – 5} \right)[/latex] to get rid of the parenthesis.
![= [(3x-5)/(x+5)(x-5)]-[(2x-10)/(x+5)(x-5)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex4_r5_c2.gif)
- Put them all together in one fraction with a common denominator of [latex]\left( {x + 5} \right)\left( {x – 5} \right)[/latex]. However, keep each numerator inside a parenthesis.
![=[(3x-5)-(2x-10)]/[(x+5)(x-5)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex4_r6_c2.gif)
- Distribute the negative sign into the parenthesis. Remember the signs will switch
Group similar terms together before simplifying them.
![=(3x-2x-5+10)/[(x+5)(x-5)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex4_r7_c2.gif)
- Compare the top and bottom expressions if there are common factors.
![=(x+5)/[(x+5)(x-5)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex4_r8_c2.gif)
- I cancel out the factor [latex]\left( {x + 5} \right)[/latex].
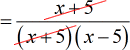
- We got it! You may include the restrictions that [latex]x \ne 5[/latex] and [latex]x \ne – \,5[/latex] based on the original denominator of the given rational expression. This is to prevent the division of zero, which is not good.
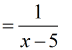
Example 5: Subtract and add the rational expressions below.
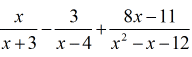
This problem is definitely interesting. To solve this, hold on to the things that you already know. Find the LCD by doing the steps below.
Factor each denominator completely and neatly line up the common factors. Identify each unique factor with the highest power.
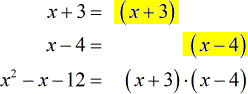
Multiply together the ones with the highest exponents for each unique factor.
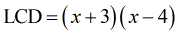
- Provide the missing factors for each denominator to reflect the LCD obtained above.
![={[x/(x+3)][(x-4)/(x-4)]}-{[3/(x-4)][(x+3)/(x+3)]}+{(8x-11)/[(x=3)(x-4)]}](https://www.chilimath.com/wp-content/uploads/2017/07/ex5_r2_c2.gif)
- Simplify by multiplication.
![={[x(x-4)]/[(x+3)(x-4)]}-{[3(x+3)]/[(x+3)(x-4)]}+{(8x-11)/[(x+3)(x-4)}](https://www.chilimath.com/wp-content/uploads/2017/07/ex5_r3_c2.gif)
- It should look like this after you distribute each constant into the parenthesis.
![={(x^2-4x)/[(x+3)(x-4)]}-{(3x+9)/[(x+3)(x-4)]}+{(8x-11)/[(x+3)(x-4)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex5_r4_c2.gif)
- Combine them in one fraction while keeping each numerator within a parenthesis. Make sure to copy the indicated operations correctly.
![=[(x^2-4x)-(3x+9)+(8x-11)]/[(x+3)(x-4)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex5_r5_c2.gif)
- To prevent any unnecessary arithmetic errors, group similar terms before simplifying them.
![=(x^2-4x-3x+8x-9-11)]/[(x+3)(x-4)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex5_r6_c2.gif)
- Now, we’ll factor out the numerator and hope to see common factors between the numerator and denominator that can be canceled.
![=(x^2+x-20)/[(x+3)(x-4)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex5_r7_c2.gif)
- Great! I see [latex]\left( {x – 4} \right)[/latex] both on top and bottom.
![=[(x+5)(x-4)]/[(x+3)(x-4)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex5_r8_c2.gif)
- Go ahead and cancel it.
![=[(x+5)(x-4)]/[(x+3)(x-4)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex5_r8_c2_cancelled.gif)
- We now have our final answer. Add the restrictions [latex]x \ne 4[/latex] and [latex]x \ne – \,3[/latex] to avoid dividing by zero.
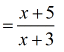
Example 6: Subtract and add the rational expressions below.
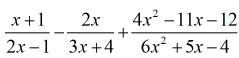
This is our last example in this lesson. I must say this is very similar to example 5. By now, you should already have a solid understanding of how to add and subtract rational expressions.
Let’s start finding the LCD again.
Factor each denominator completely and neatly line up the common factors. Identify each unique factor with the highest power.
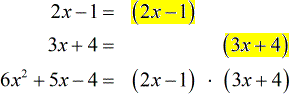
Multiply together the ones with the highest exponents for each unique factor.
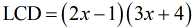
- This can be a bit messy but trust me, it will work out just fine as long as we are careful in every step.
Factor the denominator of the third rational equation completely.
![=[(x+1)/(2x-1)]-[2x/(3x+4)]+(4x^2-11x-12)/[(2x-1)(3x+4)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex6_r1_c2.gif)
- Provide the missing factors for each denominator to attain the required LCD of [latex]\left( {2x – 1} \right)\left( {3x + 4} \right)[/latex].
![={[(x+1)/(2x-1)][(3x+4)/(3x+4)]}-{[2x/(3x+4)][(2x-1)/(2x-1)]+{(4x^2-11x-12)/[(2x-1)(3x+4)]}](https://www.chilimath.com/wp-content/uploads/2017/07/ex6_r2_c2.gif)
- Multiply the fractions to simplify.
![={(3x^2+7x+4)/[(2x-1)(3x+4)]}-{(4x^2-2x)/[(2x-1)/(3x+4)]+{(4x^2-11x-12)/[(2x-1)(3x+4)]}](https://www.chilimath.com/wp-content/uploads/2017/07/ex6_r3_c2.gif)
- Place them in one huge fraction. Account for all the numerators inside each parenthesis and ensure that they have the correct indicated operations.
![=[(3x^2+7x+4)+(4x^2-2x)+(4x^2-11x-12)]/[(2x-1)(3x+4)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex6_r4_c2.gif)
- Place the similar terms side by side before combining them.
![=(3x^2-4x^2+4x^2+7x+2x-11x+4-12)/[(2x-1)(3x+4)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex6_r5_c2.gif)
- Wow! We cleaned out the numerator pretty well.
Proceed by factoring the numerator.
![=(3x^2-2x-8)/[(2x-1)(3x+4)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex6_r6_c2.gif)
- These are the correct factors of the numerator. It looks nice because we have common factors to cancel.
![=[3x+4)(x-2)]/[(2x-1)(3x+4)]](https://www.chilimath.com/wp-content/uploads/2017/07/ex6_r7_c2.gif)
- Cancel out [latex]\left( {x – 2} \right)[/latex].
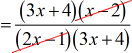
- That’s it. Simple, right?
You may also be interested in these related math lessons or tutorials:
