How to Solve Exponential Equations using Logarithms

In our previous lesson, you learned how to solve exponential equations without logarithms. This time around, we want to solve exponential equations requiring the use of logarithms. Why? The reason is that we can’t manipulate the exponential equation to have the same or common base on both sides of the equation. If you encounter such type of problem, the following are the suggested steps:

Steps to Solve Exponential Equations using Logarithms

1) Keep the exponential expression by itself on one side of the equation.

2) Get the logarithms of both sides of the equation. You can use any bases for logs.

3) Solve for the variable. Keep the answer exact or give decimal approximations. In addition to the steps above, make sure that you review the Basic Logarithm Rules because you will use them in one way or another.

This is a two-column table showing the basic or fundamental rules of the logarithms. The first rule states that the log of base 10 of b^x is equal to x times the log of base 10 of b. The second rule states that the log of base 10 of 1 is equal to zero. The third rule states that the log of base b of b equals 1. The fourth rule states that the natural logarithm of 1 is equal to zero. The fifth rule states that the natural logarithm of the natural number "e" is equal to 1. And finally, the sixth rule states that the natural logarithm of e^x is equal to x.

Let’s go over some examples!

Examples of How to Solve Exponential Equations using Logarithms

Example 1: Solve the exponential equation [latex]{5^{2x}} = 21[/latex].

The good thing about this equation is that the exponential expression is already isolated on the left side. We can now take the logarithms of both sides of the equation. It doesn’t matter what base of the logarithm to use. The final answer should come out the same. The best choice for the base of log operation is [latex]5[/latex] since it is the base of the exponential expression itself. However, we will also use in the calculation the common base of [latex]10[/latex], and the natural base of [latex]\color{red}e[/latex] (denoted by [latex]\color{blue}ln[/latex]) just to show that in the end, they all have the same answers.

  • Log Base of [latex]5[/latex]
This shows the step-by-step solutions to the exponential equation: 5^(2x) = 21. log of base 5 of [5^(2x)] = log of base 5 of 21 ==> 2x * log of base 5 of 5 = log of base 5 of 21 ==> 2x = log of base 5 of 21 ==> x = (log of base 5 of 21)/2 ==> That gives as that x is approximately equal to x ≈ 0.9458.
  • Log Base of [latex]10[/latex]
This is a complete solution to the exponential equation 5^(2x) = 21. We have 5^(2x) = 21 ==> log of base 10 of [5^(2x)] = log of base 10 of 21 ==>(2x) * log base of 10 of 5 = log base of 10 of 21 ==> 2x = (log of base 10 of 21)/(log of base 10 of 5) ==> x = [(log base 10 of 21)/(log base 10 of 5)] / 2 ≈ 0.9468. Therefore x is approximately equal to the decimal number 0.9458.
  • Log Base of [latex]e[/latex]
On the other hand, we can solve the exponential equation 5^(2x) = 21 using logarithm with the base "e", also known as the Euler's number. Here are the steps. 5^(2x) = 21 ==> ln [5^(2x)] = ln(21) ==> (2x)*(ln(5) = ln(21) ==> 2x = [ln(21)]/[ln(5)] ==> x = [ln(21)/ln(5)]/2 ==> x ≈0.9458. As you can see, we arrived at the same answer when we solved the same exponential equation using the logarithms of bases 5, 10 and e (Euler's constant).

Example 2: Solve the exponential equation [latex]2\left( {{3^{x – 5}}} \right) = 12[/latex] .

As you can see, the exponential expression on the left is not by itself. We must eliminate the number [latex]2[/latex] that is multiplying the exponential expression. To do that, divide both sides by [latex]2[/latex]. That would leave us just the exponential expression on the left, and [latex]6[/latex] on the right after simplification.

To begin solving this exponential equation, divide both sides by 2. {2[3^(x-5)]}/2 = 12/2 ==> 3^(x-5) = 6 which is a less intimidating exponential equation to work with.

It’s time to take the log of both sides. Since the exponential expression has base [latex]3[/latex], that’s the convenient base to use for log operation. In addition, we will also solve this using the natural base [latex]e[/latex] just to compare if our final results agree.

  • Log Base of [latex]3[/latex]
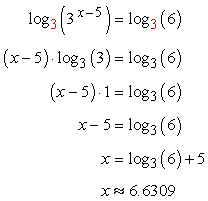
We will solve the exponential function 3^(x-5) = 6 using logarithm of base 3. log of base 3 of 3^(x-5) = log of base 3 of 6 ==> (x-5) * log of base 3 of 3 = log of base 3 of 6 ==> (x-5) = log of base 3 of 6 ==> x-5 = log of base 3 of 6 ==> x = log of base of 3 of 6 + 5 ==> x ≈6.6309. The final solution to the exponential equation is x is approximately equal to 6.6309.
  • Log Base of [latex]e[/latex]
We will solve the same exponential equation using base e (also known as the Euler's constant). ln [3^(x-5)] = ln (6) ==> (x-5) * ln(3) = ln(6) ==> x-5 = [ln(6)]/[ln(3)] ==> x = [ln(6)]/[ln(3)] + 5 ==> x≈6.6309. The final answer is x is approximately equal to 6.6309.

Example 3: Solve the exponential equation [latex]2\left({\Large{{{{{e^{4x – 3}}} \over {{e^{x – 2}}}}}}} \right) – 7 = 13[/latex] .

This looks like a mess at first. However, if you know how to start this out, the solution to this problem becomes a breeze. What we should do first is to simplify the expression inside the parenthesis. Use the Division Rule of Exponent by copying the common base of [latex]e[/latex] and subtracting the top by the bottom exponent.

We start by writing the exponential function with base "e" then solve it step by step. Here we go. 2 * { [ e^(4x-3)] / [e^(x-2) ] } -7 = 13 ==> 2 * { e ^[(4x-3)-(x-2)] } - 7 = 13 ==> 2 ^ [ e^(4x-3-x+2)] -7 = 13 ==> 2 [ e ^(3x-1) ] - 7 = 13.

Now isolate the exponential expression by adding both sides by [latex]7[/latex], followed by dividing the entire equation by [latex]2[/latex].

To continue solving the above exponential equation, we have: 2 [ e ^ (3x-1) ] =20 ==> e^(3x-1) = 10.

Take the logarithm of both sides. Use [latex]\color{red}ln[/latex] because we have a base of [latex]e[/latex]. Then solve for the variable [latex]x[/latex].

Finally, to finish it off, we will solve it as usual by getting the natural logarithm of both sides of the equations: ln [ e ^ (3x-1) ] = ln (10) ==> (3x-1) * ln (3) = ln (10) ==> (3x-1) = ln (10) ==> 3x-1 = ln (10) ==> 3x-1 = ln(10) ==> 3x = ln(10) + 1 = x = [ln(10)+1]/3 ==> x ≈ 1.1009. So that means x is approximately equal 1.1009.

Example 4: Solve the exponential equation [latex]{1 \over 2}{\left( {{{10}^{x – 1}}} \right)^x} + 3 = 53[/latex] .

Observe that the exponential expression is being raised to [latex]x[/latex]. Simplify this by applying the Power to a Power Rule. Do that by copying the base [latex]10[/latex] and multiplying its exponent to the outer exponent. It should look like this after doing so.

(1/2) * [ 10 ^ (x^2 - x) ] + 3 = 53

We can now isolate the exponential expression by subtracting both sides by [latex]3[/latex] and then multiplying both sides by [latex]2[/latex].

(1/2) * [10^(x^2-x)] + 3 = 53 ==> (1/2) * [10 ^ (x^2-x)] = 50 ==> 10^(x^2-x) = 100

Take the logarithm of both sides with base [latex]10[/latex]. If you just see a [latex]\color{red}log[/latex] without any specific base, it is understood to have [latex]10[/latex] as its base.

log [ 10 ^ (x^2-x) ] = log (100) ==> (x^2-x) * log (10) = log (100) ==> (x^2-x) = 2 ==> x^2 - x = 2

We are going to solve this quadratic equation by factoring method. Let’s move everything to the left side, therefore making the right side equal to zero. Factor out the trinomial into two binomials. Set each binomial factor equal zero then solve for [latex]x[/latex].

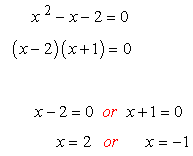
x^2-x-2 = 0 ==> (x-2)(x+1) = 0. therefore x - 2 = 0 means x =2; and x + 1 = 0 means x = -1

Example 5: Solve the exponential equation [latex]{e^{2x}} – 7{e^x} + 10 = 0[/latex].

We will need a different strategy to solve this exponential equation. Observe that we can actually convert this into a factorable trinomial. First, we let [latex]m = {e^x}[/latex]. Rewrite the exponential expression using this substitution.

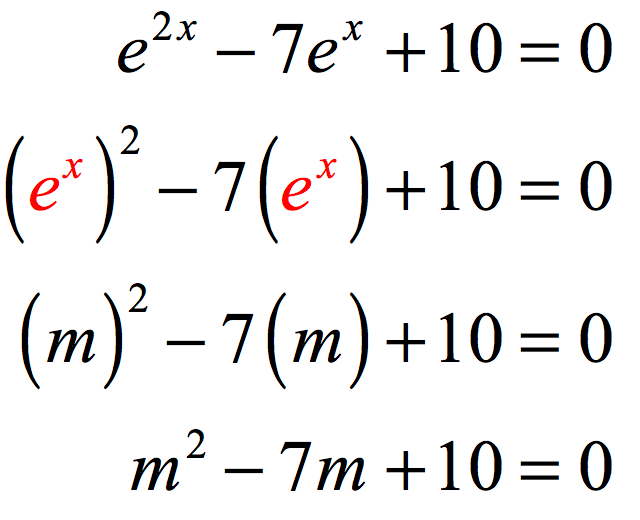
Solving the exponential equation with base "e" in quadratic form we have the follow steps: e^(2x) - 7*e^x + 10 = 0 ==> (e^x)^2 - 7 * (e^x) + 10 =10. Let m = e^x, this transforms the equation into a simpler quadratic equation where the trinomial on the left side of the equation is easily factorable. m^2 - 7m + 10 = 0.

Factor out the trinomial as a product of two binomials. Then replace [latex]m[/latex] by [latex]e^x[/latex] again.

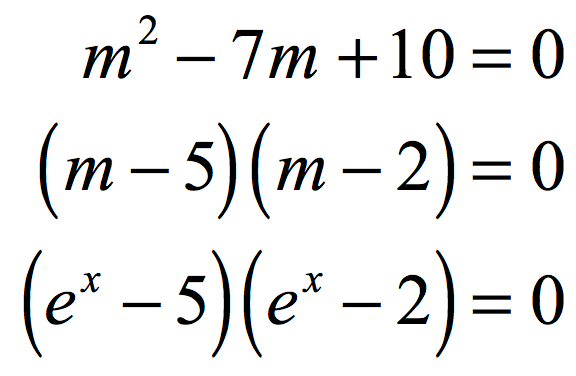
So, continuing with the solving process we get: (m-5)* (m-2) = 0. Now we can substitute back e^x for m. This gives us (e^x-5)(e^x-2) =0.

Finally, set each factor equal to zero and solve for [latex]x[/latex], as usual, using logarithms.

Now we are faced with two simple transcendental equations to solve. The first one is e^x - 5 = 0. To solve this equation we have e^x - 5 = 0 ==> e^x = 5 ==>ln(e^5) = ln(5) ==> x * ln(e) = ln(5) ==> x * 1 = ln(5) ==> x = ln(5) where x ≈ 1.6097. For the second equation, we have the transcendental equation e^x -2 = 0 ==> e^x = 2 ==> ln(e^x) = ln(2) ==> x * ln(e) = ln (2) ==> x * 1 = ln(2) ==> x = ln(2). That means x is approximately equal to 0.6932 or x ≈0.6932.

You may also be interested in these related math lessons or tutorials:

Solving Exponential Equations without Logarithms