Solving Exponential Equations with the Same Base or Like Base

An exponential equation involves an unknown variable in the exponent. In this lesson, we will focus on the exponential equations that do not require the use of logarithm. In algebra, this topic is also known as solving exponential equations with the same base. Why? The reason is that we can solve the equation by forcing both sides of the exponential equation to have the same base.

---

Key Steps in Solving Exponential Equations without Logarithms

Make the base on both sides of the equation the SAME

so that if [latex]\large{b^{\color{blue}M}} = {b^{\color{red}N}}[/latex]

then [latex]{\color{blue}M} = {\color{red}N}[/latex]

• In other words, if you can express the exponential equations to have the same base on both sides, then it is okay to set their powers or exponents equal to each other.

You should also remember the properties of exponents in order to be successful in solving exponential equations.

---

Basic Properties of Exponents

1) Zero Property

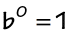
2) Negative Exponent Property

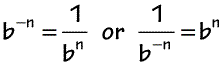
3) Product Rule

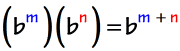
4) Quotient Rule

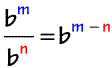
5) Power to a Power Rule

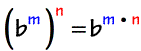
Let’s take a look at some examples!

---

Examples of How to Solve Exponential Equations without Logarithms

Example 1: Solve the exponential equation below using the Basic Properties of Exponents.

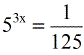
Solution:

• Given

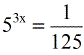
• Express the denominator of the right side with a base of [latex]5[/latex]. We have [latex]125 = {5^3}[/latex].

Apply the Negative Exponent Property.

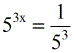
• At this point, the bases are the same therefore set the powers equal to each other.

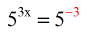
• This is just a simple one-step linear equation.

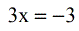
• To solve for [latex]x[/latex], divide both sides by [latex]3[/latex]. That’s it!

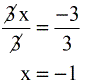
The final answer here is [latex]x = – 1[/latex].

---

Example 2: Solve the exponential equation below using the Basic Properties of Exponents.

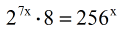
Solution:

• Given

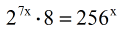
• Express all numbers with the base of [latex]2[/latex]. So we have: [latex]8 = {2^3}[/latex] and [latex]256 = {2^8}[/latex].

Apply the Product Rule on the left, while using the Power to a Power Rule on the right side.

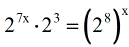
• Here we are ready to set the powers equal to each other since we are able to create single bases that are the same on both sides.

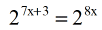
• Solve the simple linear equation.

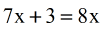
• Subtract both sides by [latex]7x[/latex] to isolate [latex]x[/latex]. Done!

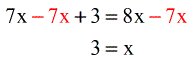
The final answer is [latex]x=3[/latex].

---

Example 3: Solve the exponential equation below using the Basic Properties of Exponents.

Solution:

• Given

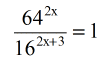
• Express each number with a base of [latex]2[/latex]. In doing so…

[latex]64 = {2^6}[/latex] and [latex]16 = {2^4}[/latex]

• Applying Power to a Power Rule.

In other words, multiply the inner exponent to the outer exponent. Do it for both the numerator and denominator.

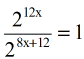
• Apply the Quotient Rule.

Subtract the top exponent by the bottom exponent.

• This is how it looks after subtracting the exponents.

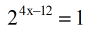
Now, looking at the right side, can we express [latex]1[/latex] as an exponential number with base [latex]2[/latex]?

The answer is yes! We can write it as [latex]1 = {2^0}[/latex] using the Zero Property of Exponent.

• Now we have the set-up that we want – having the same bases on both sides.

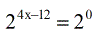
• Set the exponent of the left-hand side of the equation equal to the exponent of the right-hand side, then solve the equation for the variable [latex]x[/latex].

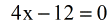
• To solve the equation, start by adding both sides by [latex]12[/latex] to move the constant to the right side.

• Finally, divide both sides by [latex]4[/latex] to get the value of [latex]x[/latex].

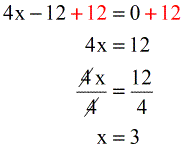
The final answer is [latex]x = 3[/latex].

---

Example 4: Solve the exponential equation below.

Solution:

• Start by writing the equation to solve.

• Express each fraction as an exponential number with a base of [latex]6[/latex].

[latex]36 = {6^2}[/latex]

[latex]6 = {6^1}[/latex]

[latex]216 = {6^3}[/latex]

[latex]\Large{\left( {{1 \over {{6^2}}}} \right)^{3 – x}}{\left( {{1 \over {{6^1}}}} \right)^x} = {6^3}[/latex]

• Apply the Negative Exponent Property on the left side of the equation.

• Multiply the inner exponents to outer exponents using the Power to a Power Rule.

• Since they have a common base, add the exponents using the Product Rule.

• It’s obvious that by having a single and the same base on both sides, we can now set each power equal to each other.

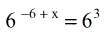
• Solve the linear equation by adding both sides by [latex]6[/latex] to get [latex]x = 9[/latex].

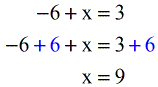
And so the solution is [latex]x = 9[/latex].

---

Example 5: Solve the exponential equation below using the Basic Properties of Exponents.

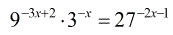
Solution:

• Given

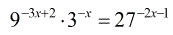
• Use [latex]3[/latex] as the common base.

[latex]9={3^2}[/latex] and [latex]27={3^3}[/latex]

• Multiply the inner and outer exponents by applying the Power to a Power Rule.

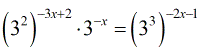
• At this point, we can add the exponents on the left side of the equation because they now have common bases.

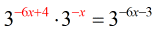
• Apply the Product Rule by adding the exponents when bases are equal.

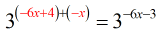
• Clearly, we can set the powers of both sides of the equation equal to each other.

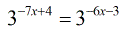
• This results in a simple multi-step equation.

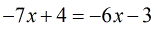
• So we add [latex]6x[/latex] first on both sides. Then, subtract by [latex]4[/latex]. And finally, divide by [latex] – 1[/latex] to fully isolate [latex]x[/latex] by itself!

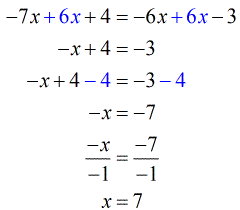
The answer is [latex]x=7[/latex]. Easy!

---

Example 6: Solve the exponential equation below using the Basic Properties of Exponents.

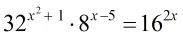
Solution:

• Given

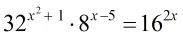
• Express each number with a base of [latex]2[/latex].

Next, multiply the inner exponents to outer exponents using the Power to a Power Rule.

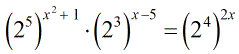
• To generate a single base on the left side, use the Product Rule – copy the common base [latex]2[/latex] and add the exponents.

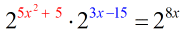
• This is when we apply the Product Rule.

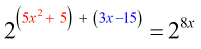
• After the addition of exponents, we have single bases on each side.

It’s time to set the powers equal to each other.

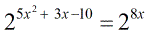
• After equating the powers, we arrive at this quadratic equation.

We need to move all terms on one side while forcing the opposite side equal to zero.

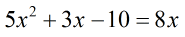
• Solve the quadratic equation using the factoring method. Factor out [latex]5[/latex] in the trinomial then factor out the simple trinomial as a product of two binomials.

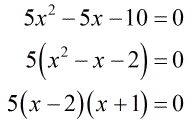
• Using the Zero Property, we get these values for [latex]x[/latex].

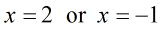
The correct answers are [latex]x = 2[/latex] and [latex]x = – 1[/latex].

---

Example 7: Solve the exponential equation below using the Basic Properties of Exponents.

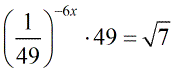
Solution:

• Given

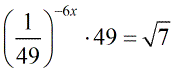
• Express each number as the exponential number with a base of [latex]7[/latex].

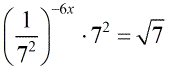
• Apply the Negative Exponent Property on the left side.

Also, the square root symbol can be rewritten as the exponent of [latex]\large{1 \over 2}[/latex].

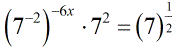
• Apply the Power to a Power Rule on the left side.

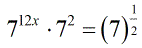
• Express the left side with a single base using the Product Rule by copying the common base and adding the exponents.

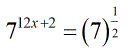
• We can now set the powers equal to each other, then solve.

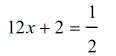
• To solve for [latex]x[/latex], subtract both sides by [latex]2[/latex].

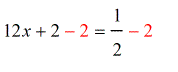
• Simplify

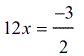
• To finish this off, divide both sides by [latex]12[/latex].

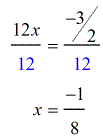
The final solution is [latex]x = – {\large{1 \over 8}}[/latex].

---

Example 8: Solve the exponential equation below using the Basic Properties of Exponents.

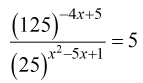
Solution:

• Given

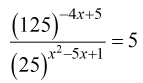
• Express the numbers using the base [latex]5[/latex].

Next, multiply the inner and outer exponents using the Power to a Power Rule.

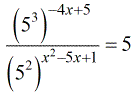
• It looks like we can use the Quotient Rule because we have the same bases on the numerator and denominator.

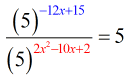
• Subtract the exponent on the numerator by the exponent in the denominator.

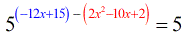
• Simplify

It’s okay now to set the “powers” or exponents equal to each other and then solve the quadratic equation.

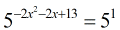
• Solve the quadratic equation by factoring the trinomial into two binomials. Then set each binomial equal to [latex]0[/latex] to solve for [latex]x[/latex].

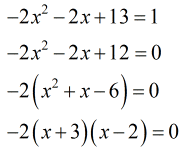
• Using the Zero Product Property, we obtain these values of [latex]x[/latex].

The final answers are [latex]x = – 3[/latex] and [latex]x = 2[/latex].

---

You may also be interested in these related math lessons or tutorials:

Solving Exponential Equations using Logarithms