Completing the Square Steps

In a regular algebra class, completing the square is a very useful tool or method to convert the quadratic equation of the form [latex]y = a{x^2} + bx + c[/latex] also known as the “standard form”, into the form [latex]y = a{(x – h)^2} + k[/latex] which is known as the vertex form.

Believe me, the best way to learn how to complete the square is by going over a few examples! The examples below will guide you step by step.

Find the Vertex Form of [latex]y = a{x^2} + bx + c[/latex] using Completing the Square

Example 1: Find the vertex form of the quadratic function below.

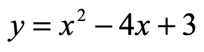
y = x^2 - 4x + 3

This quadratic equation is in the form [latex]y = a{x^2} + bx + c[/latex]. However, I need to rewrite it using some algebraic steps in order to make it look like this…

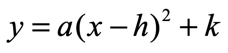
y = a(x - h)^2 + k

This is the vertex form of the quadratic function where [latex]\left( {h,k} \right)[/latex] is the vertex or the “center” of the quadratic function or the parabola.

Before I start, I realize that [latex]a = 1[/latex]. Therefore, I can immediately apply the “completing the square” steps.

STEP 1: Identify the coefficient of the linear term of the quadratic function. That is the number attached to the [latex]x[/latex]-term.

in y=x^2-4x+3, the coefficient of the x term is -4

STEP 2: I will take that number, divide it by [latex]2[/latex] and square it (or raise to the power [latex]2[/latex]).

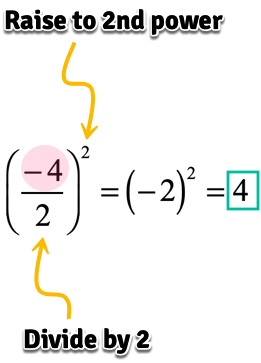
(-4/2)^2=(-2)^2=4

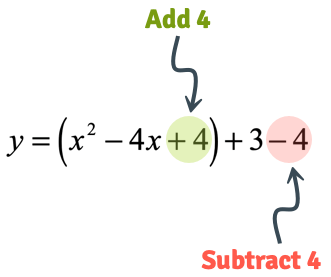
STEP 3: The output in step #2 will be added and subtracted on the same side of the equation to keep it balanced.

Think About It: If I add [latex]4[/latex] on the right side of the equation, then I am technically changing the original meaning of the equation. So to keep it unchanged, I must subtract the same value that I added on the same side of the equation.

y=(x^2-4x+4)+3-4

STEP 4: Now, express the trinomial inside the parenthesis as a square of a binomial, and simplify the outside constants.

  • After simplifying, it is now in the vertex form [latex]y = a{\left( {x – h} \right)^2} + k[/latex] where the vertex [latex]\left( {h,k} \right)[/latex] is [latex]\left( {2, – 1} \right)[/latex].
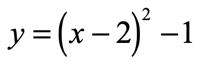
y=(x-2)^2-1
  • Visually, the graph of this quadratic function is a parabola with a minimum at the point [latex]\left( {2, – 1} \right)[/latex]. Since the value of “[latex]a[/latex]” is positive, [latex]a = 1[/latex], then the parabola opens in upward direction.
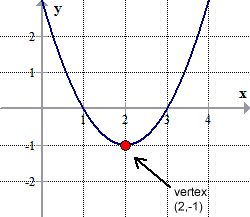
the graph of a quadratic function with a vertex at (2,-1)

Example 2: Find the vertex form of the quadratic function below.

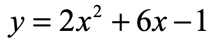
y=2x^2+6x-1

The approach to this problem is slightly different because the value of “[latex]a[/latex]” does not equal to [latex]1[/latex], [latex]a \ne 1[/latex]. The first step is to factor out the coefficient [latex]2[/latex] between the terms with [latex]x[/latex]-variables only.

STEP 1: Factor out [latex]2[/latex] only to the terms with variable [latex]x[/latex].

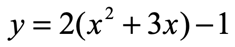
y=2(x^2+3x)-1

STEP 2: Identify the coefficient of the [latex]x[/latex]-term or linear term.

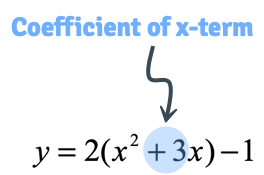
in y=2(x^2+3x)-1, the coefficient of the x term is 3

STEP 3: Take that number, divide it by [latex]2[/latex], and square.

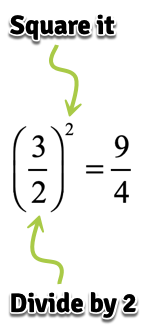
(3/2)^2=9/4

STEP 4: Now, I will take the output [latex]\large{9 \over 4}[/latex] and add it inside the parenthesis.

  • By adding [latex]\large{9 \over 4}[/latex] inside the parenthesis, I am actually adding [latex]\large2\left( {{9 \over 4}} \right) = {9 \over 2}[/latex] to the entire equation.
  • Why multiply by [latex]2[/latex] to get the “true” value added to the entire equation? Remember, I factored out [latex]2[/latex] in the beginning. So for us to find the real value added to the entire equation, we need to multiply the number added inside the parenthesis by the number that was factored out.
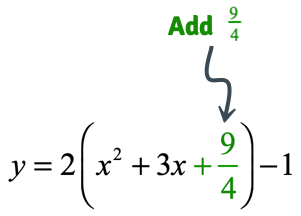
y=2(x^2+3x+9/4)-1

STEP 5: Since I added [latex]\large{9 \over 2}[/latex] to the equation, then I should subtract the entire equation by [latex]\large{9 \over 2}[/latex] also to compensate for it.

y=2(x^2+3x+9/4)-1-9/4

STEP 6: Finally, express the trinomial inside the parenthesis as the square of binomial and then simplify the outside constants. Be careful combining the fractions.

  • It is now in the vertex form [latex]y = a{\left( {x – h} \right)^2} + k[/latex] where the vertex [latex]\left( {h,k} \right)[/latex] is [latex]\large\left( {{{ – \,3} \over 2},{{ – 11} \over 2}} \right)[/latex].
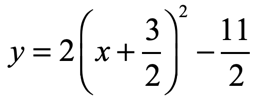
y=2(x+3/2)^2-11/2

Example 3: Find the vertex form of the quadratic function below.

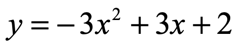
y=-3x^2+3x+2

Solution:

  • Factor out [latex] – \,3[/latex] among the [latex]x[/latex]-terms.
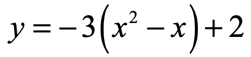
y=-3(x^2-x)+2
  • The coefficient of the linear term inside the parenthesis is [latex] – \,1[/latex]. Divide it by [latex]2[/latex] and square it. Add that value inside the parenthesis. Now, figure out how to make the original equation the same. Since we added [latex]\large{1 \over 4}[/latex] inside the parenthesis and we factored out [latex] – \,3[/latex] in the beginning, that means [latex]\large – \,3\left( {{1 \over 4}} \right) = {{ – \,3} \over 4}[/latex] is the value that we subtracted from the entire equation. To compensate, we must add [latex]\large{3 \over 4}[/latex] outside the parenthesis.
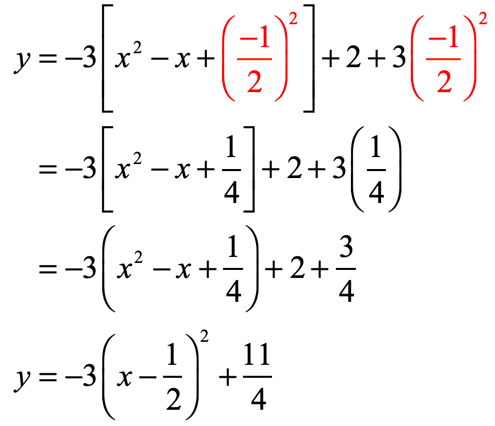
y=-3(x-1/2)^2+11/4
  • Therefore, the vertex [latex]\left( {h,k} \right)[/latex] is [latex]\large\left( {{1 \over 2},{{11} \over 4}} \right)[/latex].

Example 4: Find the vertex form of the quadratic function below.

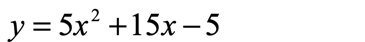
y = 5x^2 + 15x - 5

Solution:

  • Factor out [latex]5[/latex] among the [latex]x[/latex]-terms. Identify the coefficient of the linear term inside the parenthesis which is [latex]3[/latex]. Divide it by [latex]2[/latex] and square to get [latex]\large{9 \over 4}[/latex].
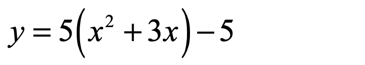
y=5(x^2+3x)-5
  • Add [latex]\large{9 \over 4}[/latex] inside the parenthesis. Since we factored out [latex]5[/latex] in the first step, that means [latex]\large5\left( {{9 \over 4}} \right) = {{45} \over 4}[/latex] is the number that we need to subtract to keep the equation unchanged.
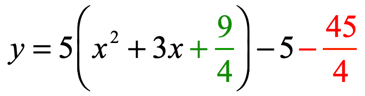
y=5(x^2+3x+9/4)-5-45/4
  • Express the trinomial as a square of binomial, and combine the constants to get the final answer.
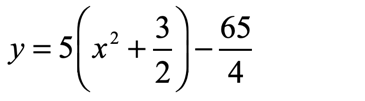
y=5(x^2+3/2)-65/4
  • Therefore, the vertex [latex]\left( {h,k} \right)[/latex] is ([latex]\large{{ – \,3} \over 2},{{ – \,65} \over 4}[/latex]).

Page 1 of 2 | Next Page