Vertex Form of a Parabola
The vertex form of a parabola is a useful way of presenting a quadratic function. In this form, we can easily identify the vertex of the parabola without doing any work. We can simply read the vertex directly from the equation.

As you can see above, if the equation of the parabola is written in vertex form
[latex]y = a{\left( {x – h} \right)^2} + k[/latex]
the coordinates of the vertex is just [latex]\left( {h,k} \right)[/latex].
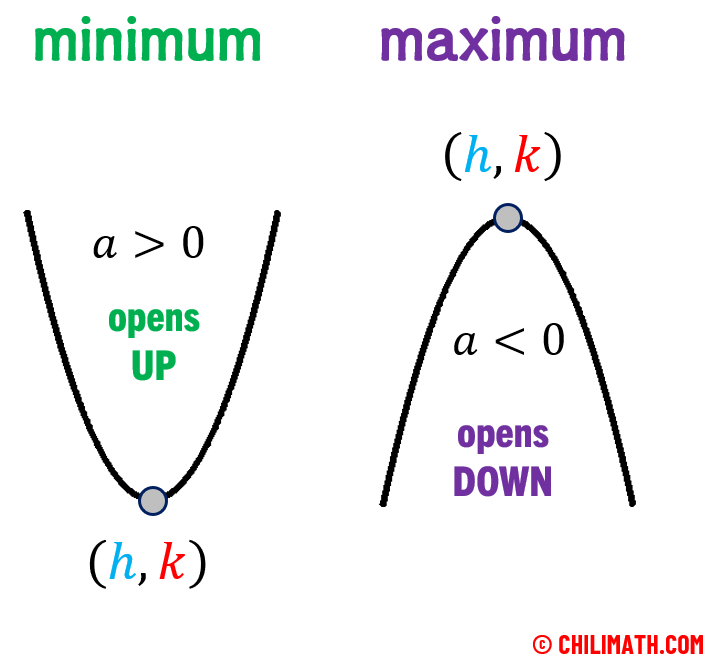
By the way, the vertex is like the “tip” of the parabola. Depending on the values of [latex]a[/latex], the vertex could either be a minimum or maximum.
If [latex]a[/latex] is positive, that is [latex]a>0[/latex], the parabola opens up and therefore it has a minimum.
If [latex]a[/latex] is negative, that is [latex]a<0[/latex], the parabola opens down and therefore it has a maximum.
Examples of the Vertex Form of Parabolas
Example 1: What is the vertex of the given parabola?
[latex]y = 2{\left( {x – 3} \right)^2} + 5[/latex]
Before we extract the vertex from the equation, we need to make sure that it is exactly of the form
[latex]y = a{\left( {x – h} \right)^2} + k[/latex]
The reason is that if we become less careful, it is possible that our signs for the coordinates of the vertex will be incorrect.
Observe that [latex]h[/latex] has a negative sign while [latex]k[/latex] is positive. If the given problem doesn’t look exactly as required, we will have to rewrite it first before we can correctly extract the vertex.
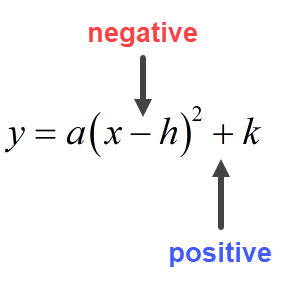
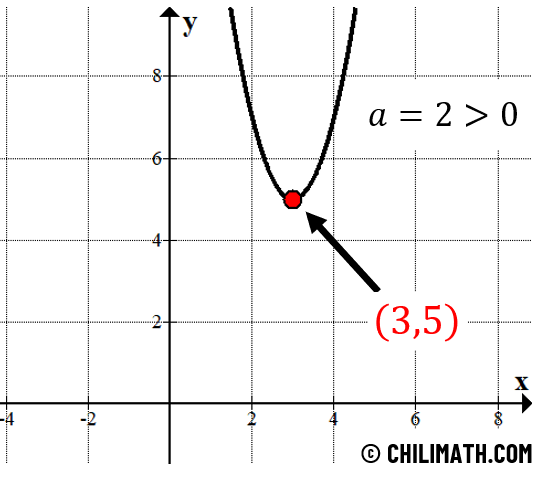
The given vertex equation of the parabola is in the form that we want. So we can claim that the vertex is [latex]\left( {3,5} \right)[/latex]. In addition, since the value of [latex]a[/latex] is positive ([latex]a>0[/latex]), it means that this vertex is a minimum.
Here’s the graph of the given parabola.
Example 2: Find the vertex of the given parabola.
[latex]y = – 2{\left( {x + 1} \right)^2} – 4[/latex]
Here is an example that if we are not careful with the signs we will get an incorrect vertex.
Let’s rewrite this such that [latex]h[/latex] is negative and [latex]k[/latex] is positive.
[latex]y = – 2{\left[ {x {\color{red}-} \left( { – 1} \right)} \right]^2} {\color{red}+} \left( { – 4} \right)[/latex]
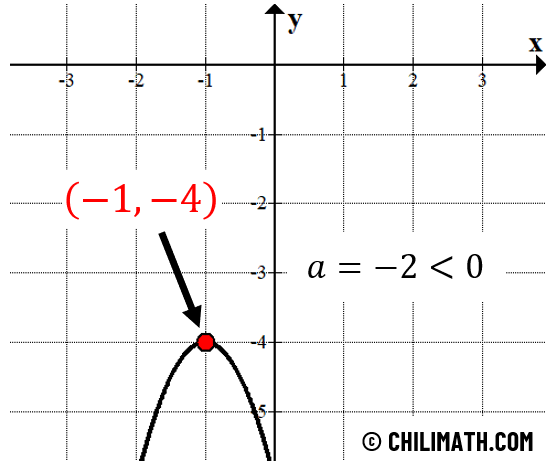
Therefore, the vertex of the parabola is [latex]\left( { – 1, – 4} \right)[/latex]. Since the value of [latex]a[/latex] is negative ([latex]a<0[/latex]), the vertex is a maximum.
Here’s the graph of the given parabola.
Example 3: Write the equation of parabola with vertex at [latex]\left( { – 2,3} \right)[/latex] and [latex]a=5[/latex].
Plugging in the value of [latex]a[/latex] is easy. We just need to be a bit careful with the vertex especially the sign of [latex]h[/latex]. Since the vertex is [latex]\left( { – 2,3} \right)[/latex], that means [latex]h=-2[/latex] and [latex]k=3[/latex]. When plugging in the values of [latex]h[/latex] and [latex]k[/latex], I will write each in a parenthesis just to be sure.
[latex]y = a{\left( {x – h} \right)^2} + k[/latex]
[latex]y = 5{\left[ {x – \left( { – 2} \right)} \right]^2} + \left( 3 \right)[/latex]
[latex]y = 5{\left( {x + 2} \right)^2} + 3[/latex]
Example 4: Find the equation of a parabola with vertex at [latex]\left( {2, – 3} \right)[/latex] and y-intercept [latex]\left( {0,1} \right)[/latex].
The first we need to do is substitute the coordinates of the vertex into the vertex form of a parabola.
The vertex is [latex]\left( {2, – 3} \right)[/latex] which means [latex]x=2[/latex] and [latex]y=-3[/latex].
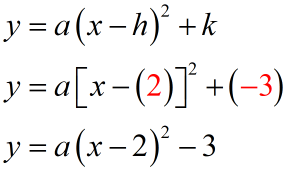
We are not given the value of [latex]a[/latex] just like in example #3 but we are provided with the y-intercept of the parabola which is [latex]\left( {0,1} \right)[/latex]. We can use this point to find the value of [latex]a[/latex].
The point [latex]\left( {0,1} \right)[/latex] implies that [latex]x=0[/latex] and [latex]y=1[/latex].
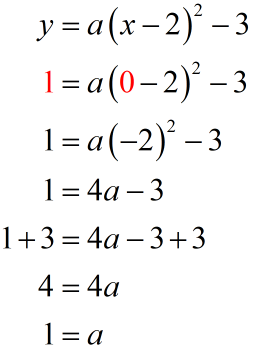
Since [latex]a=1[/latex], we can now complete the vertex form of a parabola.
[latex]y = 1{\left( {x – 2} \right)^2} – 3[/latex]
Because [latex]a[/latex] is [latex]1[/latex], we can omit it in the equation because it is understood to have [latex]1[/latex] outside the parenthesis.
Therefore, our final answer is
[latex]y = {\left( {x – 2} \right)^2} – 3[/latex]
Example 5: Find the equation of a parabola with vertex at [latex]\left( {4, 7} \right)[/latex] and through the point [latex]\left( {6,-5} \right)[/latex].
Let’s do another example for more practice. The vertex is [latex]\left( {4,7} \right)[/latex] that means [latex]h=4[/latex] and [latex]k=7[/latex]. Substitute these values in the vertex form to get
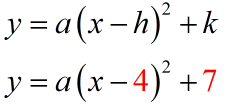
Now, let’s use the point on the parabola to solve for the value of [latex]a[/latex]. The point is [latex]\left( {6, – 5} \right)[/latex] that means [latex]x=6[/latex] and [latex]y=-5[/latex]. Substitute these values then solve for [latex]a[/latex].
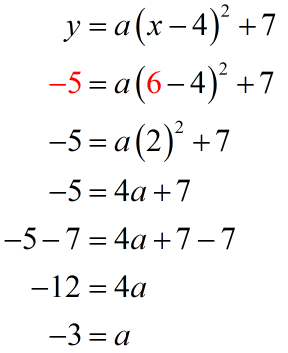
The value of [latex]a[/latex] is [latex]-3[/latex]. We can complete the vertex form of the parabola. Therefore, our final answer is
[latex]y = – 3{\left( {x – 4} \right)^2} + 7[/latex]
Example 6: Convert the standard form of a parabola into vertex form.
[latex]y = {x^2} + 8x + 14[/latex]
The standard form of a parabola is
[latex]y = a{x^2} + bx + c[/latex]
where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are real numbers but [latex]a \ne 0[/latex].
In order to rewrite the standard form into vertex form
[latex]y = a{\left( {x – h} \right)^2} + k[/latex]
we will have to perform the procedure called completing the square. So I encourage you to review my other lesson on how to complete the square.
Basically, to complete the square, take the coefficient of the [latex]x[/latex] term (linear term), and divide it by [latex]2[/latex] then square the result. Add and subtract the value (you obtained from previous steps) on the same side of the equation to keep the equation balanced. Finally, express the first three terms as square of a binomial.
So here is the linear term.

Take the coefficient of the linear term which is [latex]8[/latex], divide it by [latex]2[/latex] then square it.
[latex]{\left( {\Large{{8 \over 2}}} \right)^2} = {4^2} = 16[/latex]
Now, we will add and subtract the number [latex]16[/latex] on the same side of the equation to keep it balanced.
The first three terms will ALWAYS be a perfect square trinomial which can be factored out as a square of a binomial.
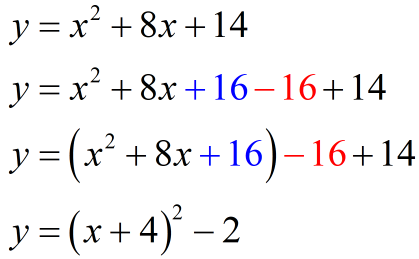
Therefore, the vertex form is [latex]y = {\left( {x + 4} \right)^2} – 2[/latex].
