More Examples of Solving Quadratic Equations using Completing the Square

In my opinion, the “most important” usage of completing the square method is when we solve quadratic equations. In fact, the Quadratic Formula that we utilize to solve quadratic equations is derived using the technique of completing the square. Here is my lesson on Deriving the Quadratic Formula.

---

Applications of Completing the Square Method

Example 1: Solve the quadratic equation below using the method of completing the square.

Move the constant to the right side of the equation, while keeping the [latex]x[/latex]-terms on the left. I can do that by subtracting both sides by [latex]14[/latex].

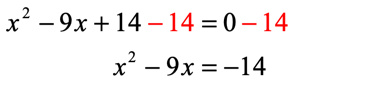
Next, identify the coefficient of the linear term (just the [latex]x[/latex]-term) which is

Take that number, divide by [latex]2[/latex] and square it.

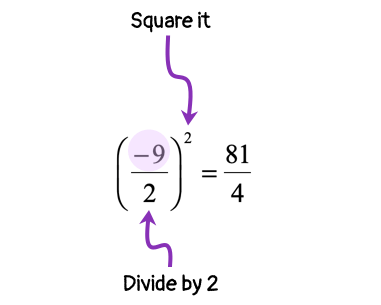
Add [latex]{{81} \over 4}[/latex] to both sides of the equation, and then simplify.

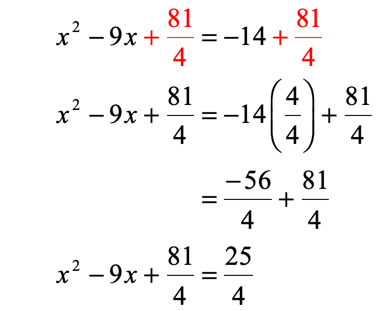
Express the trinomial on the left side as a square of binomial.

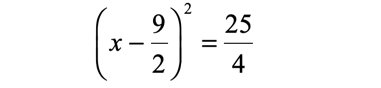
Take the square roots of both sides of the equation to eliminate the power of [latex]2[/latex] of the parenthesis. Make sure that you attach the plus or minus symbol to the constant term (right side of the equation).

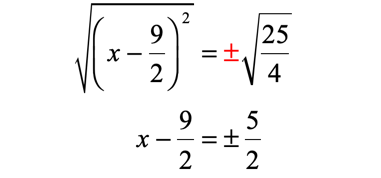
Solve for “[latex]x[/latex]” by adding both sides by [latex]{9 \over 2}[/latex].

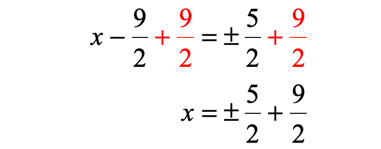
Find the two values of “[latex]x[/latex]” by considering the two cases: positive and negative.

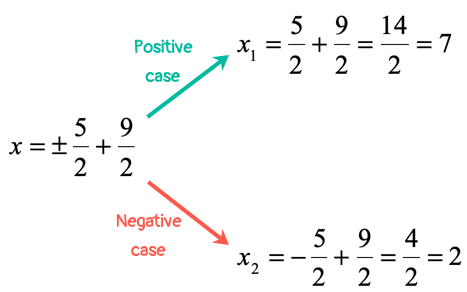
Therefore, the final answers are [latex]{x_1} = 7[/latex] and [latex]{x_2} = 2[/latex]. You may back-substitute these two values of [latex]x[/latex] from the original equation to check.

---

Example 2: Solve the quadratic equation below using the method of completing the square.

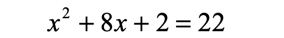
Solution:

Subtract [latex]2[/latex] from both sides of the quadratic equation to eliminate the constant on the left side.

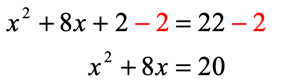
Divide [latex]8[/latex] by [latex]2[/latex] and square it.

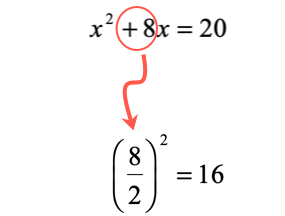
Add [latex]16[/latex] to both sides of the equation.

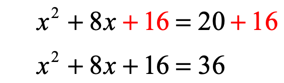
Express the left side as square of a binomial.

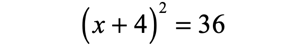
Take square roots of both sides.

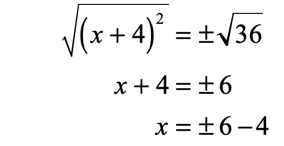
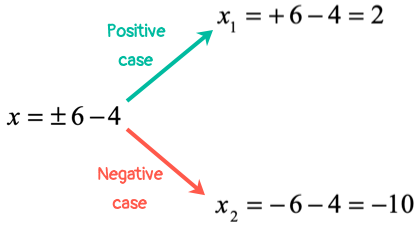
Find the two values of “[latex]x[/latex]” by considering the two cases: positive and negative.

---

Example 3: Solve the quadratic equation below using the technique of completing the square.

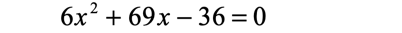
Eliminate the constant [latex] – 36[/latex] on the left side by adding [latex]36[/latex] to both sides of the quadratic equation.

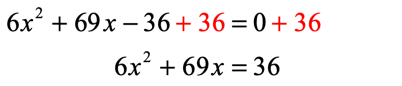
Divide the entire equation by the coefficient of the [latex]{x^2}[/latex] term which is [latex]6[/latex]. Reduce the fraction to its lowest term.

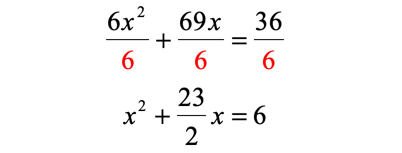
Identify the coefficient of the linear term.

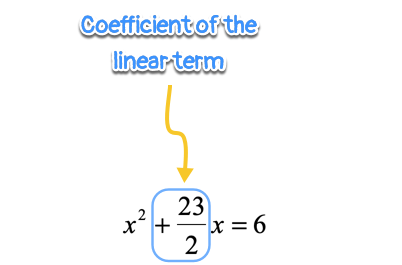
Divide this coefficient by [latex]2[/latex] and square it.

Add this output to both sides of the equation. Be careful when adding or subtracting fractions.

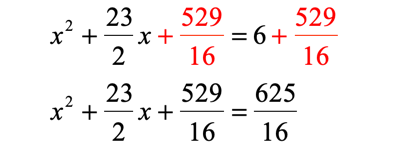
Express the trinomial on the left side as a perfect square binomial. Then solve the equation by first taking the square roots of both sides. Don’t forget to attach the plus or minus symbol to the square root of the constant term on the right side.

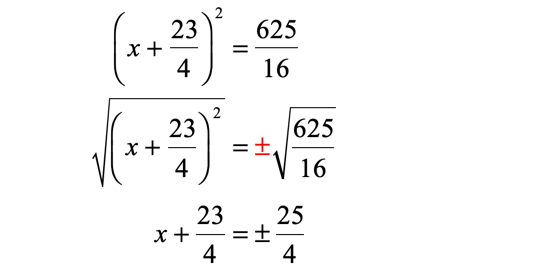
Finish this off by subtracting both sides by [latex]{{{23} \over 4}}[/latex]. You should obtain two values of “[latex]x[/latex]” because of the “plus or minus”.

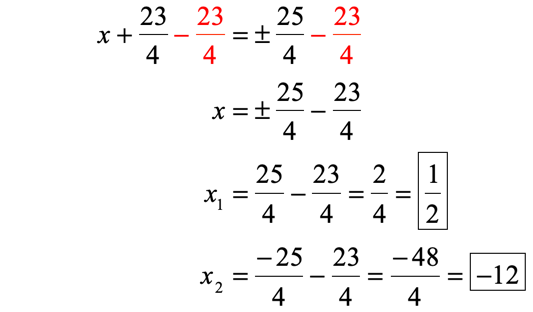
The final answers are [latex]{x_1} = {1 \over 2}[/latex] and [latex]{x_2} = – 12[/latex].

---

Example 4: Solve the quadratic equation below using the technique of completing the square.

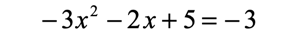
Solution:

Step 1: Eliminate the constant on the left side, and then divide the entire equation by [latex] – \,3[/latex].

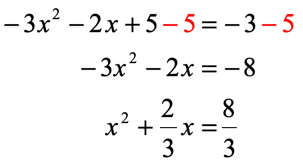
Step 2: Take the coefficient of the linear term which is [latex]{2 \over 3}[/latex]. Divide it by [latex]2[/latex] and square it.

Step 3: Add the value found in step #2 to both sides of the equation. Then combine the fractions.

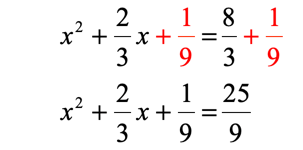
Step 4: Express the trinomial on the left side as square of a binomial.

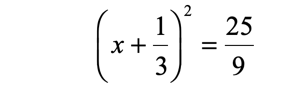
Step 5: Take the square roots of both sides of the equation. Make sure that you attach the “plus or minus” symbol to the square root of the constant on the right side. Simplify the radical.

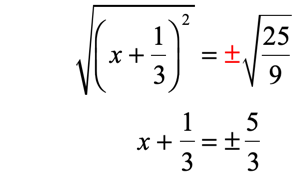
Step 6: Solve for [latex]x[/latex] by subtracting both sides by [latex]{1 \over 3}[/latex]. You should have two answers because of the “plus or minus” case.

---

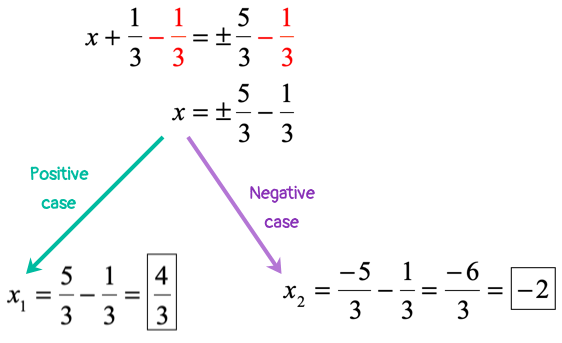
Previous Page | Page 2 of 2