Deriving the Quadratic Formula

The “horrible looking” quadratic formula below

is actually derived using the steps involved in completing the square. It stems from the fact that any quadratic function or equation of the form [latex]y = a{x^2} + bx + c[/latex] can be solved for its roots. The “roots” of the quadratic equation are the points at which the graph of a quadratic function (the graph is called the parabola) hits, crosses or touches the x-axis known as the [latex]x[/latex]-intercepts.

So to find the roots or x-intercepts of [latex]y = a{x^2} + bx + c[/latex], we need to let [latex]y = 0[/latex]. That means we have

[latex]a{x^2} + bx + c = 0[/latex]

From here, I am going to apply the usual steps involved in completing the square to arrive at the quadratic formula.

Steps on How to Derive the Quadratic Formula

Derivation of the quadratic formula is easy! Here we go.

Step 1: Let [latex]y = 0[/latex] in the general form of the quadratic function [latex]y = a{x^2} + bx + c[/latex] where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are real numbers but [latex]a \ne 0[/latex].

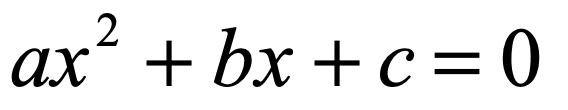
a times x squared plus b times x plus c equal zero, or in equation form, ax^2+bx+c=0

Step 2: Move the constant [latex]\color{red}c[/latex] to the right side of the equation by subtracting both sides by [latex]\color{red}c[/latex] .

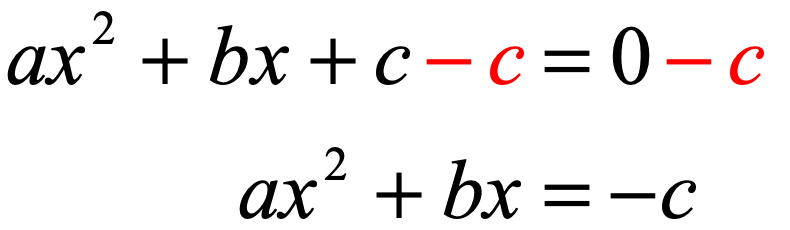
Step 3: Divide the entire equation by the coefficient of the squared term which is [latex]\large{a}[/latex].

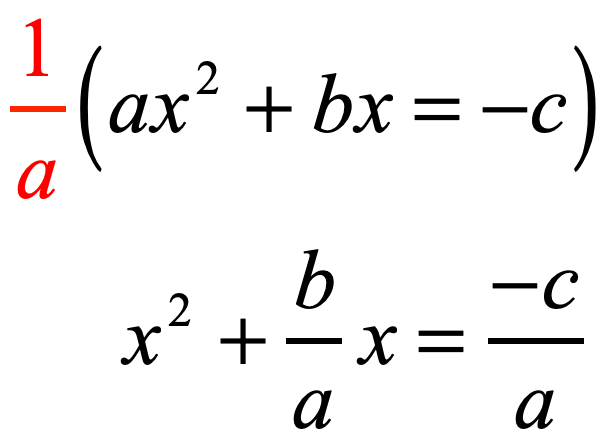
Step 4: Now identify the coefficient of the linear term [latex]\large{x}[/latex].

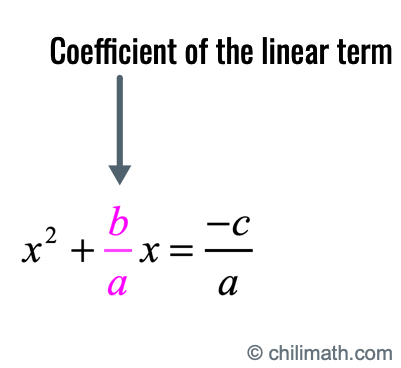
in x^2+(b/a)x=-c/a, pay attention to the coefficient of the linear term or the term with the "x" variable which is (b/a).

Step 5: Divide it by [latex]2[/latex] and raise it to the 2nd power. Then simplify it further.

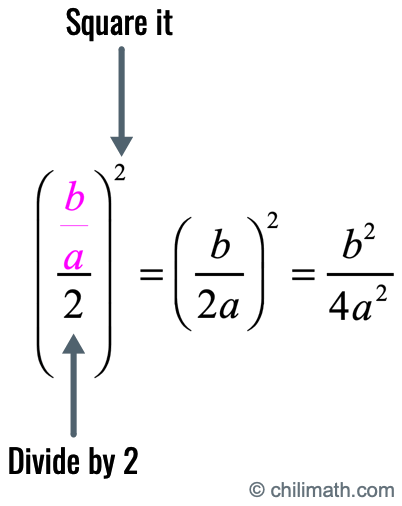
take the coefficient of the "x" term, divided it by 2 then square it. then you will have ^2 = ^2 = (b^2)/(4a^2).

Step 6: Add the output of step #5 to both sides of the equation.

add the expression b^2/(4a^2) to both sides of the equations. therefore, we have x^2 + (b/a)x + (b^2)/(4a^2) = (-c)/(a) + (b^2)/(4a^2).

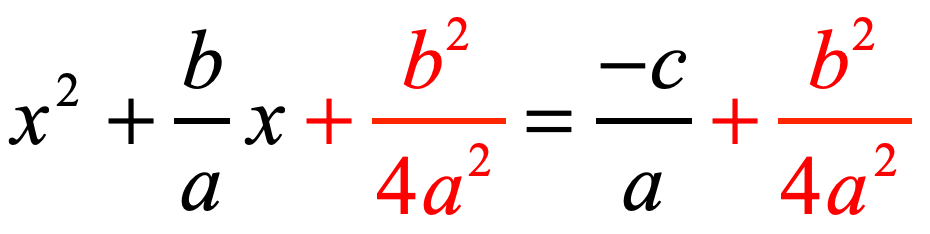
Step 7: Simplify the right side of the equation. Be careful when you add fractions with different denominators. Make sure that you find the correct Least Common Denominator (LCD) when performing addition.

x^2+(b/a)x + (b^2)/(4a^2) = (-c)/(a) + (b^2)/(4a^2) → x^2+(b/a)x + (b^2)/(4a^2) = (-4ac)/(4a^2) + (b^2)/(4a^2) → x^2+(b/a)x + (b^2)/(4a^2) = (b^2-4ac)/(4a^2).

Step 8: Express the trinomial on the left side of the equation as the square of a binomial.

express the left side of the equation as a square of a binomial. so we have [x + b/(2a)]^2 = (b^2-4ac)/(4a^2).

Step 9: Take the square root of both sides of the equation to eliminate the exponent [latex]2[/latex] of the binomial.

take the square roots of both sides of the equation. sqrt { [x + b/(2a)]^2} = sqrt{(b^2-4ac)/(4a^2)}.

Step 10: Simplify. Make sure that you attach the [latex]\color{red} \pm[/latex] on the right side of the equation. The left side no longer contains the power [latex]2[/latex].

Step 11: Keep the variable [latex]x[/latex] on the left side by subtracting both sides by [latex]\Large{b \over {2a}}[/latex].

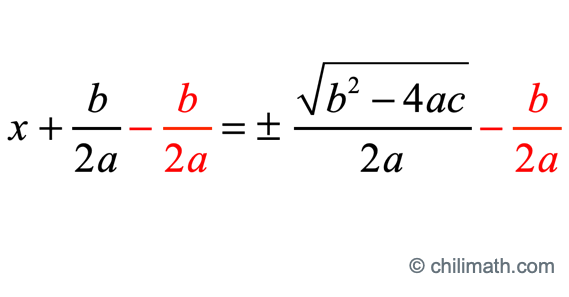
subtract both sides of the equations by b/(2a). we have x + b/(2a) - b/(2a) = ± sqrt(b^2-4ac)/(2a) - b/(2a).

Step 12: Simplify and we are done!

x = -b/(2a) ± sqrt(b^2-4ac)/(2a) → x = [-b ± sqrt (b^2 - 4ac)]/ (2a) which is the Quadratic Formula.

I hope that you find the step-by-step solution helpful in figuring out how the quadratic formula is derived using the method of completing the square.

You might be interested in:

The Quadratic Formula