Algebraic Expressions Worked Examples
There is no single method or strategy for translating mathematical phrases into algebraic expressions. As long as you remember the fundamentals, you should be able to tackle the more difficult ones. Just make sure you can justify your own algebraic expression and, more importantly, that it makes sense to you. As needed, seek assistance from your teachers or collaborate with your classmates to verify your answers.
To build your skills in writing algebraic expressions, we will go over different ways of how each operation may show up as a word or phrase in the problem. The four arithmetic operations involved are addition, subtraction, multiplication, and division.
Key Words for Addition

Key Words for Subtraction

Key Words for Multiplication

Key Words for Division

It is now time to go over some examples of algebraic expressions to practice writing them. I divide the examples into two categories:
- Basic examples of algebraic expressions
- Multi-part examples of algebraic expressions
Basic Algebraic Expressions Examples
Example 1: Write an algebraic expression for the math phrase ” the sum of a number and four”.
Solution: The word “sum” immediately gives us the hint that we are going to add here. Notice that we want to add two quantities: one unknown number and the number 4. Since we don’t know the value of the number, we can use a variable to represent it. You may use any letters of the alphabet. In this case, let’s agree to use y for the variable.
When we add the variable y and 4, we have y + 4. It is also okay to write your answer as 4 + y because addition is commutative – that is, switching the order of addition doesn’t change the sum.
The final answer is [latex]y+4[/latex].
Example 2: Write an algebraic expression for the math phrase ” 10 increased by a number”.
Solution: The keywords “increased by” imply addition. This means that an unknown number has been added to 10. Using the letter k as the variable, we can translate the statement above as 10 + k. Since addition is commutative, we can rewrite it as k + 10. Either of the two is a correct answer.
The final answer is [latex]k+10[/latex].
Example 3: Write an algebraic expression for the math phrase ” the difference of 1 and a number”.
Solution: The word “difference” suggests that we are going to subtract. In addition, when you encounter this math word (difference) make sure to pay attention to the order. The number 1 comes first then an unknown number comes in second. That means the number 1 is the minuend and the unknown number is the subtrahend. If we decide to use the letter x as our variable, the answer becomes 1 − x.
The final answer is [latex]1 – x[/latex].
Example 4: Write an algebraic expression for the math phrase ” a number less than 8″.
Solution: Be very careful when dealing with the keywords “less than”. The first quantity that comes before the “less than” keywords which is ” a number” is the subtrahend. While the quantity that comes after it becomes the minuend.
In other words, we are going to subtract the unknown number from the number 8. If we choose our variable to be the letter [latex]a[/latex], we get [latex]8 – a[/latex].
The final answer is [latex]8 – a[/latex].
Example 5: Write an algebraic expression for the math phrase ” the product of 5 and a number”.
Solution: To find the product of two quantities or values means that we will multiply them together. Selecting the letter m as our variable, the algebraic expression for this math phrase is simply 5m. It means 5 times the unknown number m.
The final answer is [latex]5m[/latex].
Example 6: Write an algebraic expression for the math phrase ” twice a number”.
Solution: The word “twice” means we are going to double something. In this case, we want to double an unknown value or quantity. Let the letter [latex]d[/latex] be the unknown number, when we double it we get the algebraic expression [latex]2d[/latex].
The final answer is [latex]2d[/latex].
Example 7: Write an algebraic expression for the math phrase ” the quotient of a number and 7″.
Solution: The keyword “quotient” means that we are performing the operation of division. We will divide an unknown number by 7. Choosing the letter [latex]w[/latex] as our variable, the math phrase above can be expressed as the algebraic expression below.
[latex]\LARGE{w \over 7}[/latex]
Example 8: Write an algebraic expression for the math phrase ” the ratio of 10 and a number”.
Solution: Similarly, the word “ratio” means division. The order here is very important. The first quantity is the number 10 and the second quantity is the unknown number. That means 10 is divided by an unknown number. Let [latex]c[/latex] be the unknown number, the algebraic expression for the math phrase above can be written as
[latex]\LARGE{10 \over c}[/latex]
Multi-Part Algebraic Expressions Examples
This time, we’ll deal with some more difficult math phrases. The algebraic expressions in this section may contain two or more operations. The basic keywords we learned earlier will serve as the foundation as we work on more difficult math phrases to translate into algebraic expressions.
Example 1: Write an algebraic expression for the math phrase ” 3 more than twice a number“.
Solution: To make this much easier to understand, we are going to divide this phrase into two parts. First, recognize that we have an unknown number. We can represent it by any letters of the alphabet. Let the unknown number be the variable [latex]x[/latex]. The diagram below should help us see what’s really going on.
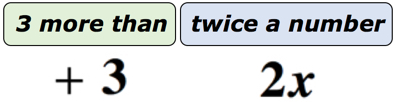
If you think about it, there is an unknown number represented by variable [latex]x[/latex] that is being doubled or multiplied by 2. Whatever is the product, we will add 3 to it. So, our final answer should look like the one below.
The final answer is [latex]2x+3[/latex].
Example 2: Write an algebraic expression for the math phrase ” the difference of half a number and 10″.
Solution: Suppose the variable [latex]y[/latex] is the unknown number. The keyword “difference” prompts us that we are going to perform subtraction. It is crucial here that we pay attention to the order of subtraction. After the word “difference”, we should expect two quantities. The first one is the minuend, while the second one is the subtrahend. Take a look at the diagram below.
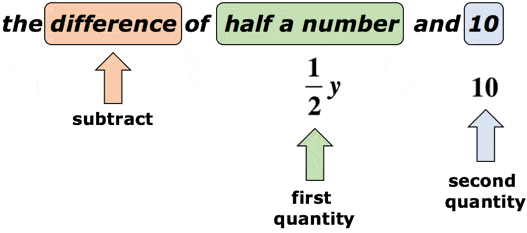
Referring to the diagram, we will subtract the first quantity by the second quantity. The final answer for the math phrase should look something like this,
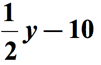
Example 3: Write an algebraic expression for the math phrase ” 7 less than the product of a number and 6″.
Solution: We know that “less than” suggests a subtraction operation. But we need to be a little bit careful here because the order of how we subtract is important. Suppose the unknown number is represented by the variable [latex]k[/latex]. Let’s put this on a diagram to make a sense of it.
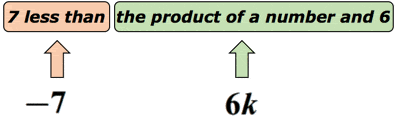
Actually, this math phrase can be rewritten as
” the product of a number and 6 minus 7 “
The “7 less than” means “minus 7” to whatever quantity being described which in this case, is “the product of a number and 6”. Here’s the final interpretation of the math phrase in an algebraic expression:
[latex]6k-7[/latex]
Example 4: Write an algebraic expression for the math phrase “the average of a number and 4”.
Solution: To begin this particular math phrase, we must first define the term “average.” To calculate the average or mean of two or more numbers, add up all the numbers to get a sum, then divide it by the number of entries or numbers. If we let [latex]m[/latex] be the variable to represent the unknown number, the math phrase above can be expressed in algebraic expressions as,
[latex]\LARGE{{m + 4} \over 2}[/latex]
Example 5: Write an algebraic expression for the math phrase ” the quotient of 1, and 1 decreased by a number”.
Solution: The keyword “quotient” means we will divide. In this case, we want to divide the number 1 by the quantity 1 decreased by a number. Below is the algebraic expression that can represent the math phrase above. Let [latex]a[/latex] be the unknown number.
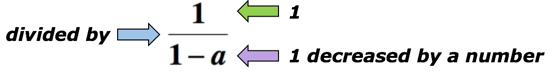
Example 6: Write an algebraic expression for the math phrase ” a third of the square of a number, increased by 2″.
Solution: There are a few things going on here. First, the part of the phrase which states ” a third of the square of a number ” can be interpreted as ” the square of a number divided by 3 “. We will need to raise the unknown number by 2 then divide it by 3. Suppose the unknown number is [latex]t[/latex], we get
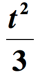
We are not done yet. The last step to do is to add the quantity above by 2 to incorporate the remaining part of the phrase ” increased by 2 “. So here’s the final representation of the given math phrase.
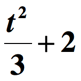
You may also be interested in these related math lessons or tutorials:
