Distance Formula Exercises

Distance Formula Practice Problems with Answers

Here are ten (10) practice exercises about the distance formula. As you engage with these problems, my hope is that you gain a deeper understanding of how to apply the distance formula. Good luck!

the distance between points A and B is the square root of the of the sum of the difference of the x coordinates and the difference of the y coordinates

Problem 1: How far is the point [latex]\left( { – 4,6} \right)[/latex] from the origin?

Answer

[latex]\color{black}2\sqrt {13} [/latex] units

Problem 2: Find the distance between the points [latex]\left( {4,7} \right)[/latex] and [latex]\left( {1, – 6} \right)[/latex]. Round your answer to the nearest hundredth.

Answer

[latex]\color{black}13.34[/latex] units

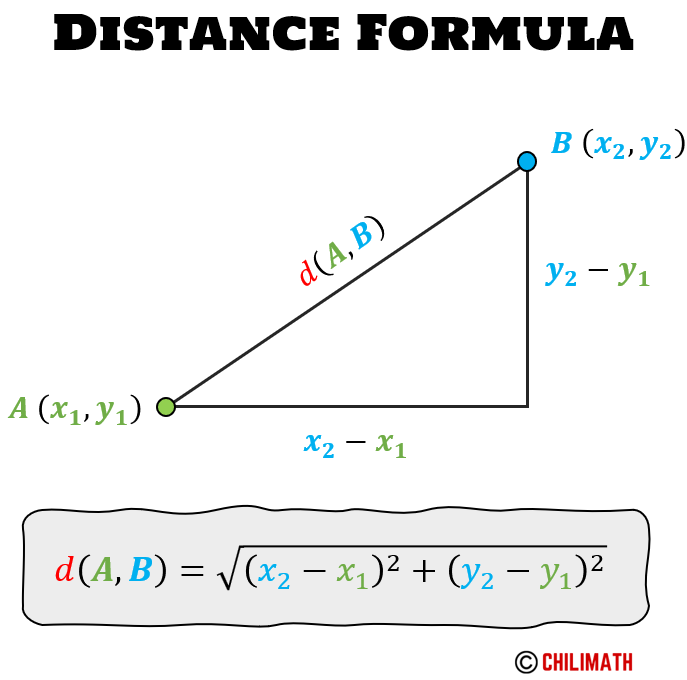
Problem 3: Find the distance between the points on the XY-plane. Round your answer to one decimal place.

two points on the xy-plane. these points are (-4,2) and (3,-3).
Answer

[latex]\color{black}8.6[/latex] units

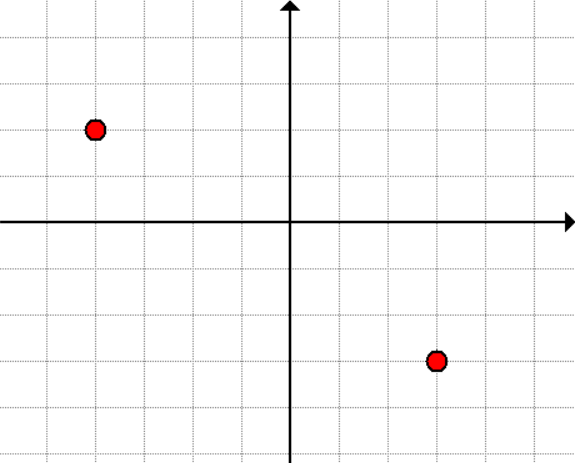
Problem 4: Determine the distance between points on the coordinate plane. Round your answer to two decimal places.

two points on the coordinate plane. the points are (0,3) and (-4,-4).
Answer

[latex]\color{black}8.06[/latex] units

Problem 5: The chord of a circle has endpoints as shown below (in green dots). What is the length of the chord?

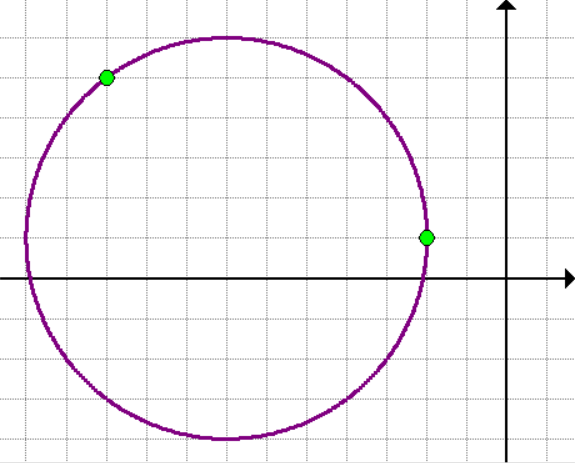
a chord of a circle with endpoints (-2,1) and (-10,5)
Answer

[latex]\color{black}4\sqrt 5[/latex] units

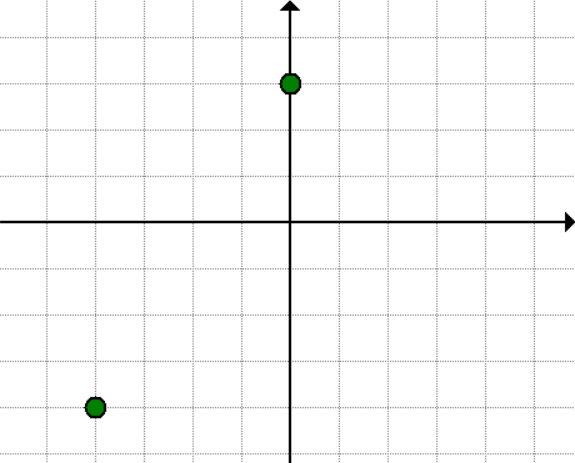
Problem 6: The diameter of a circle has endpoints as shown below (in red dots). What is the length of the diameter?

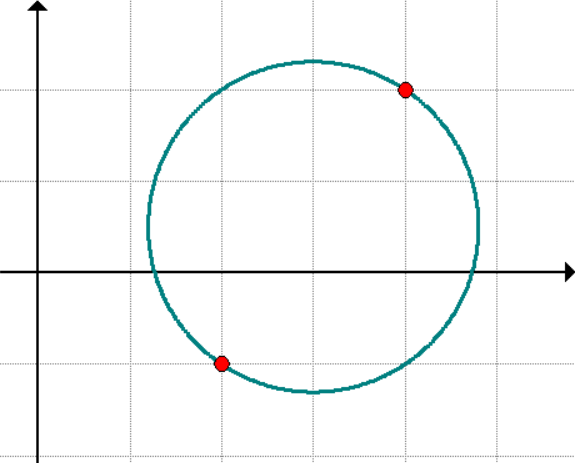
a circle with a diameter having endpoints (2,-1) and (4,2)
Answer

[latex]\color{black}\sqrt 13[/latex] units

Problem 7: Find the two points on the x-axis that are [latex]15[/latex] units away from the point [latex]\left( {-2, 9} \right)[/latex].

Answer

[latex]\left( {10,0} \right)[/latex] and [latex]\left( { – 14,0} \right)[/latex]

Problem 8: Find the two points found on the y-axis which are [latex]25[/latex] units from the point [latex]\left( {7, -5} \right)[/latex].

Answer

[latex]\left( {0,19} \right)[/latex] and [latex]\left( {0, – 29} \right)[/latex]

Problem 9: Find the values of [latex]\color{red}k[/latex] such that the points [latex]\left( {{\color{red}k}, – 1} \right)[/latex] and [latex]\left( {5, 4} \right)[/latex] have a distance of [latex]{13}[/latex] units.

Answer

[latex]{k_1} = – 7[/latex] and [latex]{k_2} = 17[/latex]

Problem 10: Find the values of [latex]\color{red}m[/latex] such that the points [latex]\left( {{\color{red}m},3} \right)[/latex] and [latex]\left( {1,{\color{red}m}} \right)[/latex] are [latex]10[/latex] units apart.

Answer

[latex]{m_1} = – 5[/latex] and [latex]{m_2} = 9[/latex]

You might also like these tutorials:

Tags: Intermediate Algebra, Lessons