Classifying Triangles by Sides
A triangle can be classified based on its characteristics. One way to classify triangles is by their sides or by comparing the lengths of the triangle’s three sides. Based on how many congruent sides a triangle has, it can either be classified as an Equilateral, Isosceles or Scalene triangle.
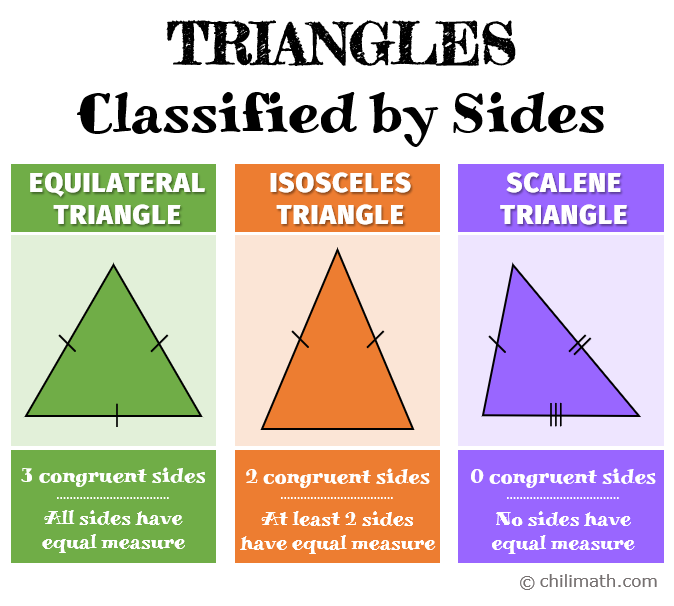
HINT: The tick marks indicate congruent sides. For example, if both sides of a triangle have the same number of tick marks, it means that both sides have the same measure.
Let’s now look at each type of triangle classified by its sides closely.
EQUILATERAL TRIANGLE – All three sides of the triangle are congruent or have an equal measure. In other words, the triangle has 3 congruent sides.
ISOSCELES TRIANGLE – At least two sides of the triangle are congruent or have an equal measure. Simply put, the triangle has 2 congruent sides
SCALENE TRIANGLE – All sides of the triangle have different measures. Thus, no sides are congruent or the triangle has 0 congruent sides
Example Problems on How to Classify Triangles by their Sides
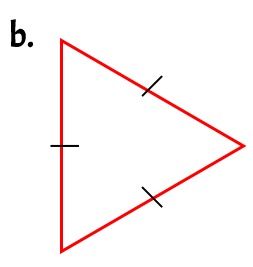
Example 1: Classify each triangle by its sides.
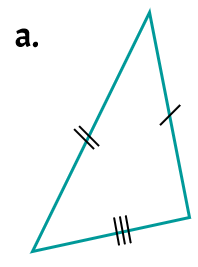
a. The tick marks on this triangle indicate that each side has a different measure. Therefore, none of the sides are congruent which makes this a scalene triangle.
b. All three sides of this triangle are congruent so this is an equilateral triangle.
Example 2: Classify the triangles given the lengths of their sides.
- Triangle M – Sides: 8 cm, 8 cm, 3 cm
- Triangle K – Sides: 2 in., 2 in., 2 in.
- Triangle P – Sides: 4 ft, 7 ft, 7 ft
- Triangle V – Sides: 5 mm, 10 mm, 6 mm
Triangle M: Since at least two sides have the same equal measure, this triangle is an isosceles triangle.
Triangle K: This is an equilateral triangle because all sides are congruent.
Triangle P: Two out of the three sides of this triangle measure 7 ft. Thus, it is an isosceles triangle.
Triangle V: It is obvious that this is a scalene triangle. It has 0 congruent sides because the triangle has different side lengths.
Example 3: What is the measure of [latex]\overline {AC} [/latex]?
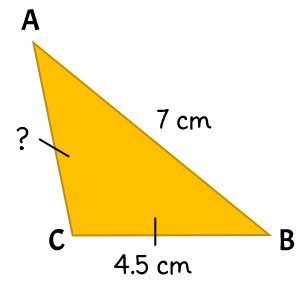
At first look, we can immediately tell that this is an isosceles triangle. Why? Because the tick marks tell us that there are two congruent sides, i.e. [latex]\overline {AC}[/latex] and [latex]\overline {CB} [/latex].
TIP: Do not assume immediately that the side lengths of the triangle are congruent based on appearance. They must be marked as congruent (look for the tick marks) or if the measurements are not already given, measure them to check the length of each side.
So far we are given two measurements:
- [latex]\overline {AB}[/latex] = 7 cm
- [latex]\overline {CB} [/latex] = 4.5 cm
Our task now is to determine the length of [latex]\overline {AC} [/latex]. However, since we know that [latex]\overline {CB} [/latex] and [latex]\overline {AC} [/latex] are congruent ([latex]\overline {CB} \cong \overline {AC} [/latex]), this means that their measures are the same.
Therefore, the length of [latex]\overline {AC} [/latex] is 4.5 cm.
You may also be interested in these related math lessons or tutorials:
