Classifying Triangles by Angles
Aside from classifying triangles by their sides, triangles can also be classified based on their angle measures. That is, we must first identify what types of angles make up a triangle before we can determine whether it is an Acute, Equiangular, Obtuse, or Right triangle.
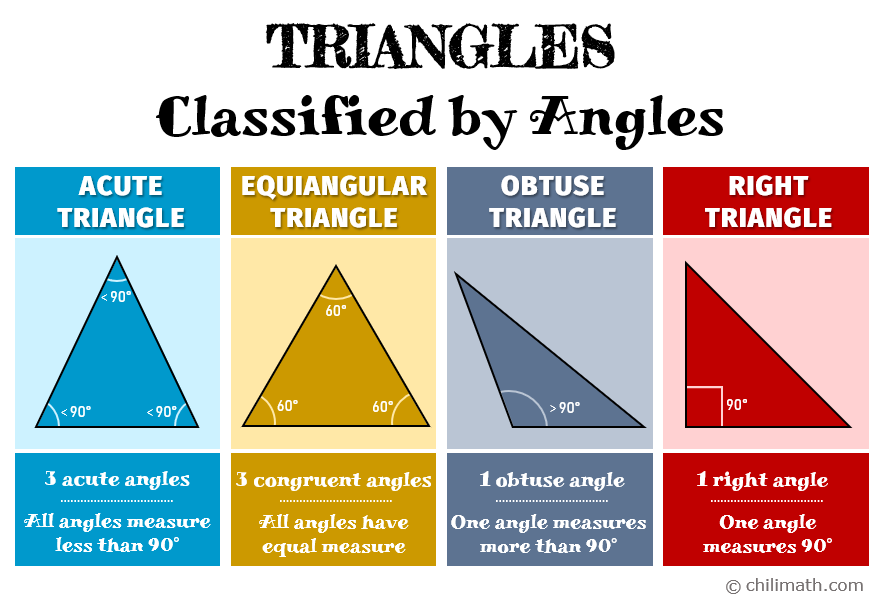
Let’s take a closer look at each type of triangle that results from classifying triangles by their angles.
ACUTE TRIANGLE
It is comprised of 3 acute angles, which means that all of its angles measure less than [latex]90^\circ[/latex].
EQUIANGULAR TRIANGLE
All angles of the triangle have the same or equal measure. In other words, it is made up of 3 congruent angles.
OBTUSE TRIANGLE
The triangle has 1 obtuse angle, which means that one of the three angles measures more than [latex]90^\circ[/latex].
RIGHT TRIANGLE
Contrary to an obtuse triangle, this triangle has 1 right angle. This tells us that one of the three angles measures exactly [latex]90^\circ[/latex].
Example Problems on How to Classify Triangles by their Angles
Example 1: Classify the triangle by its angle measures.
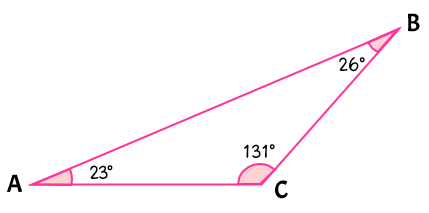
If we examine the angle measures closely, we can see that the triangle is composed of two angles that measure less than [latex]90^\circ[/latex] (acute angles) and one that is more than [latex]90^\circ[/latex] (obtuse angle).
Since one of the angle measures is more than 90 degrees, this is an obtuse triangle.
Example 2: Classify the triangle by its angle measures.
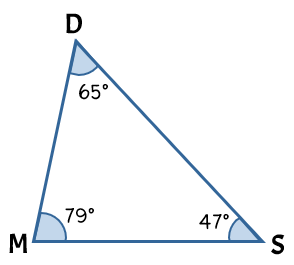
Here we have a triangle that is made up of acute angles. How can I tell? Because all three angles measure less than [latex]90^\circ[/latex].
Therefore, this is an acute triangle.
Example 3: Find the two missing angle measures of the equiangular triangle.
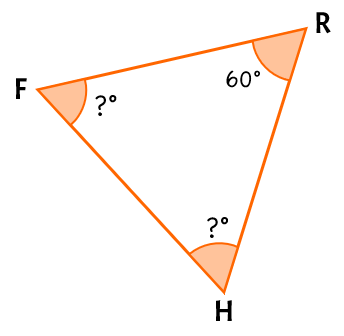
Right off the bat, we are told that this is an equiangular triangle. This means that all of the angles are congruent or have the same measure.
In that case, both [latex]\angle \,F[/latex] and [latex]\angle \,H[/latex] also measure 60 degrees ([latex]60^\circ[/latex]).
Example 4: Classify [latex]\Delta \,ZNK[/latex] and [latex]\Delta \,ZGQ[/latex].
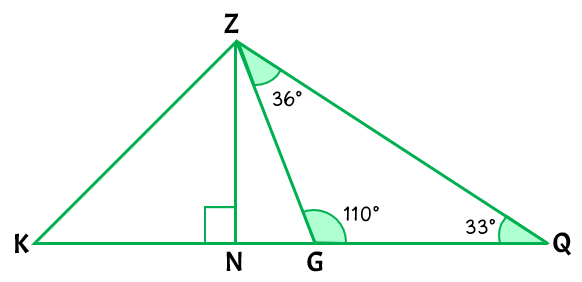
Let’s first look at [latex]\Delta \,ZNK[/latex]. Immediately, you can tell that this is a right triangle. How? Well, we see a right-angle symbol which is indicated by a small square “[latex]\square[/latex]”. When you see this symbol, it tells you that the angle is a right angle or that it measures exactly [latex]90^\circ[/latex]. And since the triangle has one right angle, then it is classified as a right triangle.
Next, we’ll take a look at [latex]\Delta \,ZGQ[/latex]. Here we are given the measures of all three angles, one of which is more than [latex]90^\circ[/latex] or is an obtuse angle. In particular, [latex]\angle \,G[/latex] measures [latex]110^\circ[/latex]. Therefore, [latex]\Delta \,ZGQ[/latex] is an obtuse triangle.
You may also be interested in these related math lessons or tutorials:
