Multiplying Complex Numbers
The process of multiplying complex numbers is very similar when we multiply two binomials using the FOIL Method. The only difference is the introduction of the expression below.
[latex]\sqrt { – 1} = i[/latex]
But also, if we square both sides of this equation we get
[latex]\sqrt { – 1} = i[/latex]
[latex]{\left( {\sqrt { – 1} } \right)^2} = {\left( i \right)^2}[/latex]
[latex] – 1 = {i^2}[/latex]
This brings us to the conclusion that these two equations mean exactly the same thing. In other words, they are equivalent equations.
Important: Don’t forget the equivalence of the two equations below. You will need it over and over.

Let’s go over some examples!
Examples of How to Multiply Complex Numbers
Example 1: Find the product of the complex numbers below.
[latex]\large{\left( {2 + 5i} \right)\left( {4 – 3i} \right)}[/latex]
Multiply the two binomials using FOIL or any method you prefer. You will have the opportunity to combine like terms. Then replace any instance of i 2 by –1. After doing so, you may need to combine similar terms again especially the new numbers that arise from substituting of i 2 by –1.
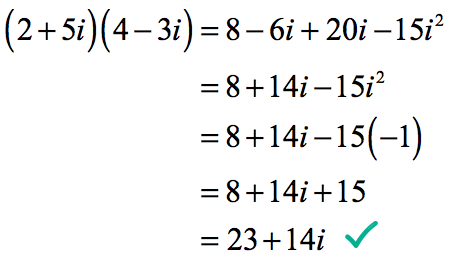
Example 2: Find the product of the complex number below and its conjugate.
[latex]\large{5 – 2i}[/latex]
The conjugate of the complex number is the same number but you switch or change the sign of the imaginary component, that is, just the [latex]\color{red}bi[/latex] term.

Therefore, the conjugate of the given complex number [latex]5 – 2i[/latex] must be [latex]5 + 2i[/latex]. We can now multiply them to get the product.
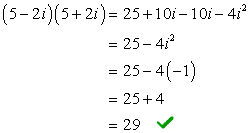
Example 3: Simplify the square of the complex number below.
[latex]\large{{\left( { – 1 – i} \right)^2}}[/latex]
The exponent of [latex]2[/latex] implies that we are going to multiply the expression inside the parenthesis by itself. Be careful with the signs when you multiply each term. Remember, negative times negative is positive, etc.
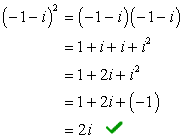
Example 4: Find the product of the complex numbers below.
[latex]\large{\left( {3i – 4{i^2}} \right)\left( { – 2i + 3{i^2}} \right)}[/latex]
Notice that each term has the expression [latex]\large\color{red}i[/latex] attached to it. Don’t panic when you see something like this in your homework. Treat it just like the previous problems.
- Start with FOIL
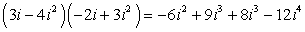
- Combine like terms
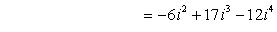
- We know that i 2 = –1. Factor the imaginary terms using this.
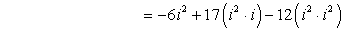
- Replace i 2 by –1.

- Simplify to get the final answer.
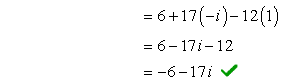
You may also be interested in these related math lessons or tutorials:
