How to Divide Complex Numbers
To divide complex numbers, write the problem in fraction form first. From there, it will be easy to figure out what to do next. Another step is to find the conjugate of the denominator. Just in case you forgot how to determine the conjugate of a given complex number, see the table below:
Conjugate of a Complex Number

Use this conjugate to multiply the numerator and denominator of the given problem then simplify. You may need to learn or review the skill on how to multiply complex numbers because it will play an important role in dividing complex numbers.
You will observe later that the product of a complex number with its conjugate will always yield a real number. The imaginary part drops from the process because they cancel each other.
It is much easier than it sounds. Here are some examples!
Examples of How to Divide Complex Numbers
Example 1: Divide the complex numbers below.
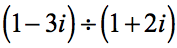
The first step is to write the original problem in fractional form.
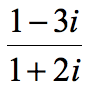
Since our denominator is [latex]1 + 2i[/latex], its conjugate is equal to [latex]1 – 2i[/latex]. Remember to change only the sign of the imaginary term to get the conjugate.
We take this conjugate and use it as the common multiplier of both the numerator and denominator.
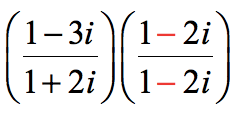
From here, we just need to multiply the numerators together and the denominators as well. Use the FOIL Method when multiplying the binomials. Perform all necessary simplifications to get the final answer.
Don’t forget to use the fact that [latex]{i^2} = – 1[/latex].
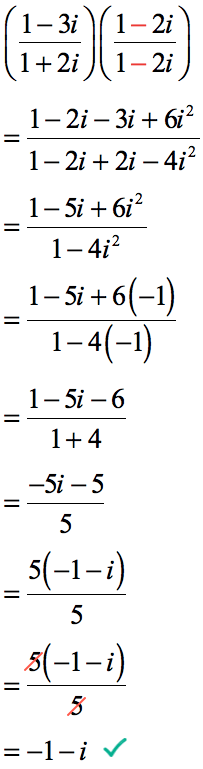
Example 2: Divide the complex numbers below.
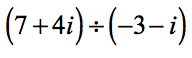
Rewrite the problem as a fraction.
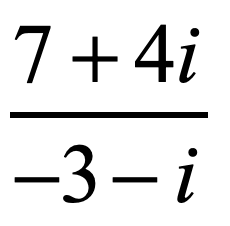
Since the denominator is [latex] – \,3 – i[/latex], its conjugate equals [latex] – \,3 + i[/latex]. Multiply the top and bottom of the fraction by this conjugate.
Towards the end of the simplification, cancel the common factor of the numerator and denominator. In this process, the common factor is [latex]5[/latex].
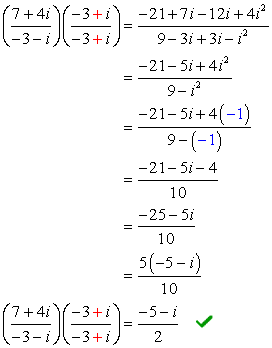
Example 3: Find the quotient of the complex numbers below.
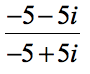
The problem is already in the form that we want, that is, in fractional form. The conjugate of the denominator [latex] – \,5 + 5i[/latex] is [latex] – 5 – 5i[/latex].
Let’s multiply the numerator and denominator by this conjugate, and simplify.
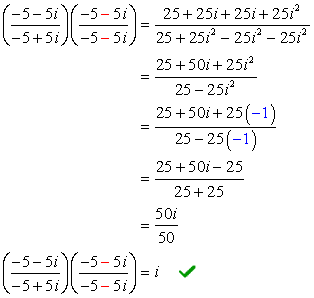
Example 4: Find the quotient of the complex numbers below.
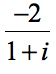
Since the denominator is [latex]1 + i[/latex], its conjugate must be [latex]1 – i[/latex]. Multiply the top and bottom of the fraction by this conjugate and simplify.
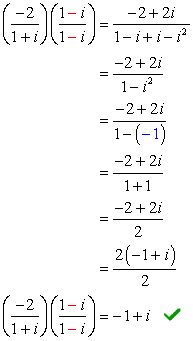
You may also be interested in these related math lessons or tutorials:
