How to Find the Determinant of a 2×2 Matrix

Suppose we are given a square matrix [latex]A[/latex] with four elements: [latex]a[/latex], [latex]b[/latex], [latex]c[/latex], and [latex]d[/latex].

Matrix A is a 2x2 matrix with elements a and b on the first row, and elements c and d on the second row. We can write this is math format as A = [a,b;c,d].

The determinant of matrix A is calculated using the following formula:

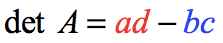
The determinant of matrix A is equal to the difference of the product of elements a and b, and the product of elements b and c. In short, this can be written as det A = a*d - b*c.

If you can’t see the pattern yet, this is how it looks when the elements of the matrix are color-coded.

  • We take the product of the elements from top left to bottom right, then subtract by the product of the elements from top right to bottom left.

If you want additional practice problems on finding the determinant of a 2×2 matrix, please click the link below.

Determinant of 2×2 Matrix Practice Problems with Answers

The Determinant of 2 x 2 Matrix (animated)

det A = det [a, d; b, c] = ad-bc

Examples of How to Find the Determinant of a 2×2 Matrix

Example 1: Find the determinant of the matrix below.

Matix A contains the entries 1 and 2 on its first row; entries 3 and 4 on its second row. Rewriting this matrix in compact form we have A = [1,2;3,4].

This is an example where all elements of the 2×2 matrix are positive.

the determinant of matrix [1,2;3,4] = (1)(4) - (2)(3) = 4 - 6 = -2

Example 2: Calculate the determinant of the matrix below.

Matrix B has entries -5 and -4 on the first row, and entries -2 and -3 on the second row. In short, matrix B = [-5,-4;-2,-3].

Here is an example of when all elements are negative. Make sure to apply the basic rules when multiplying integers. Remember, the product of numbers with the same sign will always be positive. On the contrary, if the signs are different the product will be negative.

The determinant of the matrix [-5,-4;-2,-3] is calculated by finding the product of -5 and -3 subtracted by the product of -4 and -2 which results to 7. That means, the determinant of matrix [-5,-4;-2,-3] = (-5)(-3) - (-4)(-2) = (15) - (8) = 7.

Example 3: Evaluate the determinant of the matrix below.

Matrix C is a 2 by 2 square matrix with elements -1 and -2 on the first row; elements 6 and 3 on the second row. Therefore we can write this matrix as C = [-1,-2;6,3].

Make sure to remember the rules on how to subtract integers. That is, when you subtract integers, you change the operation from subtraction to addition but you must switch the sign of the number directly found to its right (it’s called the subtrahend) then proceed with regular integer addition.

the determinant of matrix C can be solved as follows: det C = det [-1,-2;6,3] = (-1)(3) - (-2)(6) = (-3) - (-12) = -3 + 12 = 9

Example 4: Determine the determinant of the matrix below.

Matrix D has elements 5 and -3 on its first row; elements x and y on its second row. Writing this matrix on short form, we have D = [5,-3;x,y].

You may also encounter a problem where some of the elements in the matrix are variables. Treat this just like a normal determinant problem. Plug those variables in the designated spots in the formula then simplify as usual.

the determinant of matrix D can be solved as det [5,-3;x,y] = (5)(y)-(-3)(x) = 5y+3x

Example 5: Find the value of [latex]\color{red}\large{x}[/latex] in the matrix below if its determinant has a value of [latex]-12[/latex].

matrix of [-4,2;-8,x]

This is not a “trick” question. We can actually find the value of [latex]x[/latex] such that when we apply the formula we get [latex]-12[/latex].

Get the determinant of the given matrix then set it equal to [latex]-12[/latex]. By doing so, we generate a simple linear equation that is solvable for [latex]x[/latex].

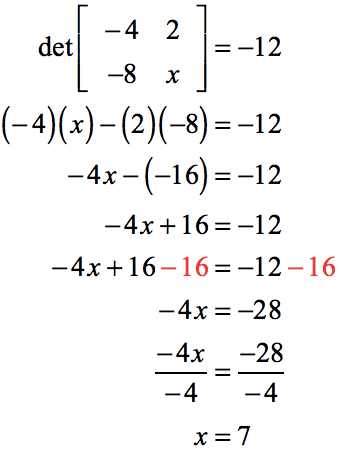
(-4)(x)-(2)(-8)=-12; the value of x is 7

Checking our answer:

Replace [latex]\color{red}\large{x}[/latex] by [latex]7[/latex], then calculate the determinant. We expect to get [latex]-12[/latex].

the determinant of the matrix [-4,2;-8,7] is -12

This verifies that our solution is correct!

You may also be interested in these related math lessons or tutorials:

Determinant 2×2 Matrix Problems with Answers

Determinants of a 3×3 Matrix

Determinant of 3×3 Matrix Problems with Answers

Cramer’s Rule 2×2

Cramer’s Rule 3×3