Subtracting Integers
If you know how to add integers, I’m sure that you can also subtract integers. The key step is to transform an integer subtraction problem into an integer addition problem. The process is very simple. Here’s how:
Steps on How to Subtract Integers
Step 1: Transform the subtraction of integers problem into addition of integers problem. Here’s how:
- First, keep the first number (known as the minuend).
- Second, change the operation from subtraction to addition.
- Third, get the opposite sign of the second number (known as the subtrahend)
- Finally, proceed with the regular addition of integers.
Step 2: Proceed with the regular addition of the integers.
Note that you will eventually add integers. So for your convenience, here’s a quick summary of the rules on how to add integers.
- Case 1: Adding two integers having the same sign
Add their absolute values then keep the common sign.
- Case 2: Adding two integers with different signs
Subtract their absolute values (larger absolute value minus smaller absolute value) then take the sign of the number with the larger absolute value.
Examples of Integer Subtractions
Example 1: Subtract the integers below.
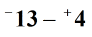
Solution:
We will need to transform the problem from subtraction to addition. To do that, we keep the first number which is –13, change the operation from subtraction to addition, then switch the sign of + 4 to –4.
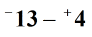
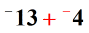
The final step is to proceed with regular addition. Add their absolute values. Then we determine the sign of the final answer. Since we are adding integers with the same sign, we will keep the common sign which in this case is negative.
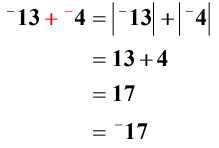
Example 2: Subtract the integers below.
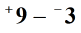
Solution:
Just like before, convert a subtraction problem to an addition problem. Positive 9 remains, switch the operation from “minus” to “plus” then get the opposite sign of the subtrahend (second number) from negative to positive.
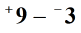

Now, let’s add them. We are adding two positive integers so we expect the answer to be positive as well because the common sign is positive.
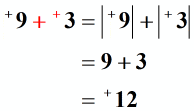
Example 3: Find the difference of the two integers.
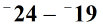
Solution:
I hope you are already getting the hang of it. Let’s make this an addition of integers problem first then proceed with regular addition of integers with different signs.
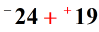
So we subtract their absolute values first then get the sign of the number with larger absolute value.
Subtracting the absolute values, we have 24 minus 19 which gives us +5. But the final answer is – 5 because the sign comes from –24.
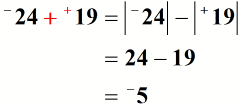
You may also be interested in these related math lessons or tutorials:
