Dividing Integers

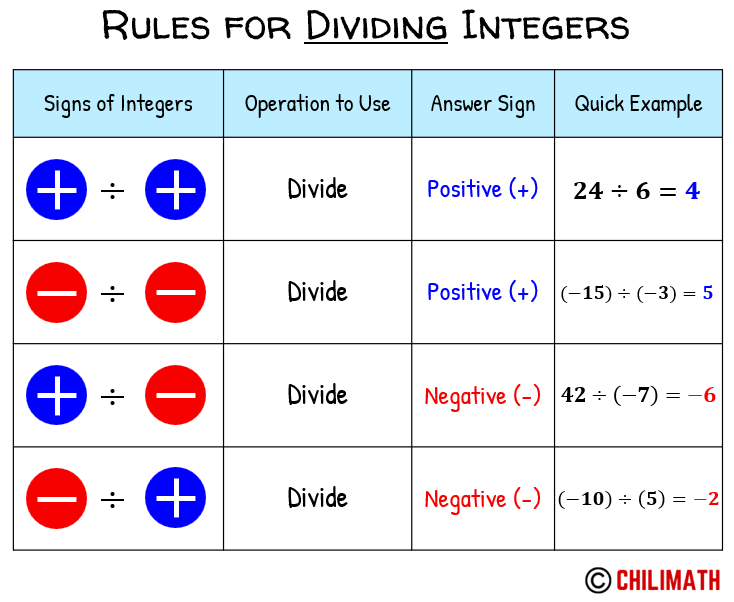
Below is a quick summary for the rules of dividing integers.

rules for dividing integers or integer divisions the quotient of two integers is always positive if the signs are the same. if their signs are different then the quotient is negative.

Now that you’ve learned how to multiply integers, dividing integers should be a breeze. The reason is that they follow very similar rules.

Rules on How to Divide Integers

Step 1: Divide their absolute values.

Step 2: Determine the sign of the final answer (known as a quotient) using the following conditions.

  • Condition 1: If the signs of the two numbers are the same, the quotient is always a positive number.
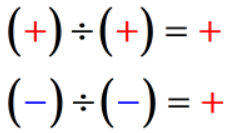
This illustration shows the rules of dividing integers with the same sign. For the first case, a positive integer divided by another positive integer is always positive. On the other hand, a negative integer divided by another negative integer is always positive. Simply put, the quotient of two integers with the same sign will always yield a positive integer solution.
  • Condition 2: If the signs of the two numbers are different, the quotient is always a negative number.
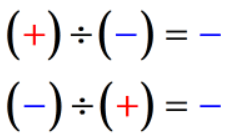
This diagram shows the rules that govern when we divide two integers with different signs. The first case implies that a positive integer divided by a negative integer results to an answer of an integer with a negative sign. Likewise, a negative integer divided by a positive integer outputs an integer with a negative sign as well. In summary, the quotient of two integers with different signs will always yield a negative integer solution.

Examples of Integer Divisions

Example 1: Divide the two integers below.

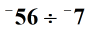
find the quotient of negative 56 and negative 7 that is -5/(-7)

Solution: First, find the absolute values of the two integers.

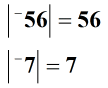
the absolute value of negative 56 is equal to positive 56 while the absolute value of negative 7 is positive 7.

Next, divide the numbers or find their quotient.

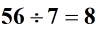
the quotient of positive 56 and positive 7 is positive 8 which can also be written as 56/7=8

Finally, determine the final sign of the answer or quotient. Because we are dividing two integers with the same sign, the quotient will have a positive sign.

-56/(-7)=+8

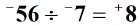
Example 2: Divide the two integers below.

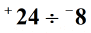
positive 24 divided by negative 8 which can also be written numerically as +24/(-8)

Solution: Divide the absolute values of the two integers.

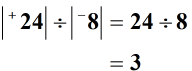
the quotient of the absolute value of +24 and the absolute value of -8 is +3

Following the rules stated above, when dividing integers with different signs the final answer (quotient) is negative.

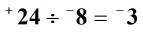
positive 24 divided by negative 8 equals negative 3, which can also be written as +24/(-8)=-3

Example 3: Divide the three integers below from left to right

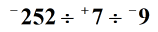
this integer division problem requires a multi-step solution: negative 252 divided by positive 7 divided by negative 9, which can also be written as -252/(+7)/(-9)

Solution: To divide three or more integers, it is important that we perform the division operation from left to right. In addition, we can accomplish it by dividing two integers at a time. The parenthesis shows the first two integers to divide, and whatever is the result or quotient will be divided by the next one. So we have here, – 252 divided by + 7 is equal to – 36. It is a negative quotient since we are dividing two integers that have different signs. Then we take that quotient and divide it by the integer that follows. We get –36  ÷ –9 = + 4. The answer is positive since we are dividing integers with the same sign.

-252/(+7)/(-9)=[(-252)/(+7)]/-9=(-36)/-9=+4

You may also be interested in these related math lessons or tutorials:

Dividing Integers Practice Problems with Answers

Integer Addition

Integer Subtraction

Integer Multiplication