Cramer’s Rule for a 3×3 System (with Three Variables)
In our previous lesson, we studied how to use Cramer’s Rule with two variables. Our goal here is to expand the application of Cramer’s Rule to three variables usually in terms of [latex]\large{x}[/latex], [latex]\large{y}[/latex], and [latex]\large{z}[/latex]. I will go over five (5) worked examples to help you get familiar with this concept.
To do well on this topic, you need to have an idea of how to find the determinant of a 3⨉3 matrix. So, this is what we are going to do first. Ready?
Formula to Find the Determinant of a 3⨉3 Matrix
- Given a 3⨉3 matrix
![Matrix A is a 3 by 3 square matrix with elemenys a, b and c on the first row, elements d, e and f on the second row, and elements g, h and i on the third row. We can write Matrix in compact for as A = [a,b,c;d,e,f;g,h,i].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_det.gif)
- Its determinant can be calculated using the following formula.
![The determinant of matrix A = [a,b,c;d,e,f;g,h,i] is calculated as as follows: |A| = a times the determinant of matrix [e,f;h,i] minus b times the determinant of matrix [d,f;g,i] plus c times the determinant of matrix [d,e;g,h]. In compact form, the determinat of matrix A is |A| = a*|e,g;h,i| - b*|d,f;g,i| + c*|d,e;g,h|.](https://www.chilimath.com/wp-content/uploads/2017/02/det-3x3-mat.gif)
Let’s do a quick example of this.
Find the determinant of matrix A
![Matrix A is a 3x3 square matrix with entries 6, 2 and -4 on its first row, entries 5, 6 and -2 on its second row, and entries 5,2 and -3 on its third row. Therefore we can write matrix A as A = [6,2,-4;5,6,-2;5,2;-3].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_detex.gif)
Solution: Make sure that you follow the formula on how to find the determinant of a 3×3 matrix carefully, as shown above. More so, don’t rush when you perform the required arithmetic operations in every step. This is where common errors usually occur, but it can be prevented. When you do it right, your solution should be similar to the one below.
![To find the determinant of the square (3 by 3) matrix A = [6,2,-4;5,6,-2;5,2,-3], we have the following steps: |A|=|6,2,-4;5,6,-2;5,2,-3|=6*|6,-2;2,-3| - (2)*|5,-2;5,-3|+(-4)*|5,6;5,2| = 6(-14) - 2(-5) - 4(-20) = -84 +10 + 80 = 6. Therefore, the determinant of matrix A is equal to 6.](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_detex2.gif)
Now, it’s time to go over the procedure on how to use Cramer’s Rule in a linear system involving three variables.
Cramer’s Rules for Systems of Linear Equations with Three Variables
- Given a linear system

- Labeling each of the four matrices
coefficient matrix:
![The coefficient-matrix D is a square matrix with elements a1,b1 and c1 on the first row; elements a2, b2 and c2; and elements a3, b3 and c3. We can write coefficient-matrix D in compact form as D = [a1,b1,c1;a2,b2,c2;a3,b3,c3].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_cmat.gif)
X – matrix:
![The x-matrix D is a square matrix with elements d1,b1 and c1 on the first row; elements d2, b2 and c2; and elements d3, b3 and c3. X-matrix D can be written as Dx = [d1,b1,c1;d2,b2,c2;d3,b3,c3].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_xmat.gif)
Y – matrix:
![The y-matrix D is a square matrix with elements a1,d1 and c1 on the first row; elements a2,d2 and c2; and elements a3, d3 and c3. Y-matrix D can be written as Dy = [a1,d1,c1;a2,d2,c2;a3,d3,c3].](https://www.chilimath.com/wp-content/uploads/2020/02/Dy.gif)
Z – matrix:
![The z-matrix D is a square matrix with elements a1,b1 and d1 on the first row; elements a2,b2 and d2; and elements a3, b3 and d3. Z-matrix D can be written as Dz = [a1,b1,d1;a2,b2,d2;a3,b3,d3].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_zmat.gif)
- To solve for [latex]x[/latex]:
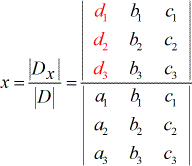
- To solve for [latex]y[/latex]:
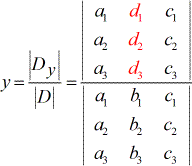
- To solve for [latex]z[/latex]:
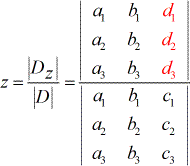
Things to observe from the setup above:
1) The coefficients of variables [latex]x[/latex], [latex]y[/latex], and [latex]z[/latex] make use of subscripted [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex], respectively. While the constant terms use subscripted [latex]d[/latex].
2) The denominators to find the values of [latex]x[/latex], [latex]y[/latex], and [latex]z[/latex] are all the same which is the determinant of the coefficient matrix (coefficients coming from the columns of [latex]x[/latex], [latex]y[/latex], and [latex]z[/latex]).
3) To solve for [latex]x[/latex], the coefficients of the [latex]x-[/latex]column is replaced by the constant column (in red).
4) To solve for [latex]y[/latex], the coefficients of the [latex]y-[/latex]column is replaced by the constant column (in red).
5) In the same manner, to solve for [latex]z[/latex], the coefficients of the [latex]z-[/latex]column is replaced by the constant column (in red).
Examples of How to Solve Systems of Linear Equations with Three Variables using Cramer’s Rule
Example 1: Solve the system with three variables by Cramer’s Rule.
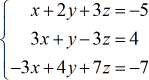
From the given system of linear equations, I will construct the four matrices that will be used to solve for the values of [latex]\large{\color{green}x}[/latex], [latex]\large{\color{green}y}[/latex], and [latex]\large{\color{green}z}[/latex].
Use the guide above to correctly set up these special matrices.
- coefficient matrix
![The coefficient matrix D has entries 1, 2 and 3 on its first row; entries 3, 1 and -3 on its second row; -3, 4 and 7 on its third row. This can be expressed as D = [1,2,3;3,1,-3;-3,4,7].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex1_d.gif)
- X – matrix
![The x-matrix D has entries -5, 2 and 3 on its first row; entries 4, 1 and -3 on its second row; -7, 4 and 7 on its third row. This can be expressed as Dx = [-5,2,3;4,1,-3;-7,4,7].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex1_dx.gif)
- Y – matrix
![The y-matrix D has entries 1, -5 and 3 on its first row; entries 3, 4 and -3 on its second row; -3, -7 and 7 on its third row which can be expressed symbolically as Dy = [1,-5,3;3,4,-3;-3,-7,7].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex1_dy.gif)
- Z – matrix
![The z-matrix D has elements 1, 2 and -5 on the first row; elements 3, 1 and 4 on the second row; -3, 4 and -7 on the third row. This can be written in math form as Dz = [1,2,-5;3,1,4;-3,4,-7].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex1_dz.gif)
Next, I will solve for the determinant of each matrix. To do this, I can manually solve the determinant of each matrix on paper using the formula provided above. It can be tedious, but it’s okay since good math skills are developed by doing lots of problems.
The values of the determinants are listed below.
Determinants of each matrix:
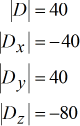
The final answers or solutions are easily computed or calculated once all the required determinants are found.
Solved values for [latex]\large{\color{green}x}[/latex], [latex]\large{\color{green}y}[/latex], and [latex]\large{\color{green}z}[/latex].
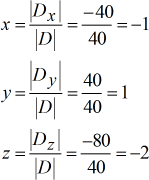
The final answer written in point notation is [latex]\color{blue}\left( {x,y,z} \right) = \left( { – 1,1, – 2} \right)[/latex].
Example 2: Solve the system with three variables by Cramer’s Rule.
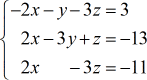
I actually consider the coefficient matrix as the “primary” matrix because the other three matrices are derived from it. For instance, the [latex]x-[/latex]matrix is just the “primary” matrix with the [latex]x-[/latex]column replaced by the constant column (in red). You can observe that the same pattern is applied in constructing the other matrices: [latex]y[/latex] and [latex]z[/latex].
- coefficient matrix
![Coefficient matrix D has elements -2, -1 and -3 on its first row; elements 2, -3 and 1 on its second row; elements 2, 0 and -3 on its third row. This can be expressed as D = [-2,-1,-3;2,-3,1;2,0,-3].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex2_d.gif)
- X – matrix
![X-matrix D or Dx has elements 3, -1 and -3 on its first row; elements -13, -3 and 1 on its second row; elements -11, 0 and -3 on its third row. This can be expressed as Dx = [3,-1,-3;-13,-3,1;-11,0,-3].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex2_dx.gif)
- Y – matrix
![Y-matrix D or Dy has elements -2, 3 and -3 on its first row; elements 2, -13 and 1 on its second row; elements 2, -11 and -3 on its third row. This can be expressed as Dy = [-2,3,-3;2,-13,1;2,-11,-3].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex2_dy.gif)
- Z – matrix
![Z-matrix D or Dz has elements -2, -1 and 3 on its first row; elements 2, -3 and -13 on its second row; elements 2, 0 and -11 on its third row. This can be expressed as D = [-2,-1,3;2,-3,-13;2,0,-11].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex2_dz.gif)
After solving the determinant of each matrix, I have them all written down.
Determinants of each matrix:
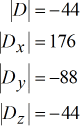
The values for [latex]x[/latex], [latex]y[/latex] and [latex]z[/latex] are calculated as follows. Notice that [latex]x[/latex] is obtained by taking the determinant of the [latex]x-[/latex]matrix divided by the determinant of the coefficient matrix. This rule holds for the rest.
Solved values for [latex]\large{\color{green}x}[/latex], [latex]\large{\color{green}y}[/latex], and [latex]\large{\color{green}z}[/latex].
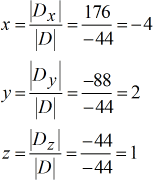
Our final answer is [latex]\color{blue}\left( {x,y,z} \right) = \left( { – \,4,2,1} \right)[/latex].
Example 3: Solve the system with three variables by Cramer’s Rule.
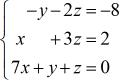
This problem is much easier than the first two examples because of the presence of zero entries in the [latex]x[/latex], [latex]y[/latex], and constant columns. Do you see it? When we have zero entries in a matrix, the calculation of its determination is dramatically simplified.
In fact, as you increase the number of zeroes in a square matrix, the work done to find its determinant is greatly reduced.
Here are the matrices extracted from the system of linear equations.
- coefficient matrix
![Coefficient matrix D can be written in compact form as D = [0,-1,-2;1,0,3;7,1,1] which means that the first row has the elements 0, -1 and -2, the second row has elements 1, 0, and 3, and finally the third row has elements 7, 1 and 1.](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex3_d.gif)
- X – matrix
![X-matrix D can be written in compact form as Dx = [-8,-1,-2;2,0,3;0,1,1] which means that the first row has the elements -8, -1 and -2, the second row has elements 2, 0, and 3, and finally the third row has elements 0, 1 and 1.](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex3_dx.gif)
- Y – matrix
![Y-matrix D can be written in compact form as Dy = [0,-8,-2;1,2,3;7,0,1] which means that the first row has the elements 0, -8 and -2, the second row has elements 1, 2, and 3, and finally the third row has elements 7, 0 and 1.](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex3_dy.gif)
- Z – matrix
![Z-matrix D can be written in compact form as Dz = [0,-1,-8;1,0,2;7,1,0] which means that the first row has the elements 0, -1 and -8, the second row has elements 1, 0, and 2, and finally the third row has elements 7, 1 and 0.](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex3_dz.gif)
Solving for their determinants, I got the following values.
Determinants of each matrix:
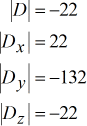
This leads us to easily set up and calculate the final answers.
Solved values for [latex]\large{\color{green}x}[/latex], [latex]\large{\color{green}y}[/latex], and [latex]\large{\color{green}z}[/latex].
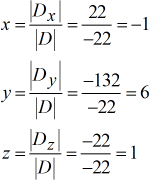
The final answer is [latex]\color{blue}\left( {x,y,z} \right) = \left( { – \,1,6,1} \right)[/latex].
Example 4: Solve the system with three variables by Cramer’s Rule
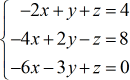
Write down the four special matrices.
- coefficient matrix
![The coefficient matrix D in math or symbolic form is D = [-2, 1, 1; -4, 2, -1; -6, -3, 1].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex4_d.gif)
- X – matrix
![The X-matrix D in math or symbolic form is Dx = [4, 1, 1; 8, 2, -1; 0, -3, 1].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex4_dx.gif)
- Y – matrix
![The Y-matrix D in math or symbolic form is Dy = [-2, 4, 1; -4, 8, -1; -6, 0, 1].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex4_dy.gif)
- Z – matrix
![The Z-matrix D in math or symbolic form is Dz = [-2, 1, 4; -4, 2, 8; -6, -3, 0].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex4_dz.gif)
Evaluate each matrix to find its determinant.
These are the determinants of each matrix:
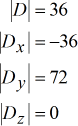
Use the Cramer’s Rule to get the following solutions.
Solved values for [latex]\large{\color{green}x}[/latex], [latex]\large{\color{green}y}[/latex], and [latex]\large{\color{green}z}[/latex].
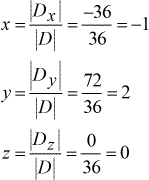
The final answer is [latex]\color{blue}\left( {x,y,z} \right) = \left( { – \,1,2,0} \right)[/latex].
Example 5: Solve the system with three variables by Cramer’s Rule
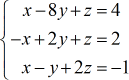
Let’s do one final example! I hope that at this point, you have had enough practice on how to solve systems with three variables using Cramer’s Rule.
I suggest that you solve this on paper first and then come back to compare your answer. When you are ready, scroll down to see the solution.

Construct the four special matrices.
- coefficient matrix
![The first matrix is called the coefficient matrix D where the first row contains the entries of 1, -8 and 1; and the second row contains the entries of -1, 2 and 1; and the third row contains the elements of 1, -1 and 2. We can write this coefficient matrix D in condense or compact for as D = [1, -8, 1; -1, 2, 1; 1, -1, 2].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex5_d.gif)
- X – matrix
![The second matrix is called the X- matrix D where the first row contains the entries of 4, -8 and 1; and the second row contains the entries of 2, 2 and 1; and the third row contains the elements of -1, -1 and 2. We can write this X-matrix D in condense or compact for as Dx = [4, -8, 1; 2, 2, 1; -1, -1, 2].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex5_dx.gif)
- Y – matrix
![The third matrix is called the Y-matrix D where the first row contains the elements of 1, 4 and 1; and the second row contains the elements of -1, 2 and 1; and the third row contains the elements of 1, -1 and 2. We can write this Y-matrix D in condense or compact for as Dy = [1, 4, 1; -1, 2, 1; 1, -1, 2].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex5_dy.gif)
- Z – matrix
![The fourth matrix is called the Z-matrix D where the first row contains the elements of 1, -8 and 4; and the second row contains the entries of -1, 2 and 2; and the third row contains the entries of 1, -1 and -1. We can write this Z-matrix D in condense or compact for as Dy = [1, -8, 4; -1, 2, 2; 1, -1, -1].](https://www.chilimath.com/wp-content/uploads/2017/02/3x3_ex5_dz.gif)
Find the determinant of each square matrix.
Determinants of each matrix
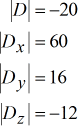
Solve for [latex]x[/latex], [latex]y[/latex] and [latex]z[/latex] using the given formula.
Solved values for [latex]\large{\color{green}x}[/latex], [latex]\large{\color{green}y}[/latex], and [latex]\large{\color{green}z}[/latex].
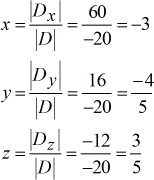
Done! The final answer in point form is [latex]\color{blue}\left( {x,y,z} \right) = {\large{\left( { – \,3, – {4 \over 5},{3 \over 5}} \right)}}[/latex].
You may also be interested in these related math lessons or tutorials:
