Algebraic Properties of Equality
Here is a quick summary of the Properties of Equality.

1) Reflexive Property of Equality
For any number [latex]a[/latex], [latex]a=a[/latex].
[latex]\Rightarrow[/latex] It states that any quantity is equal to itself.
Examples:
[latex]2=2[/latex] [latex]\\[/latex]
[latex]1+4=1+4[/latex] [latex]\\[/latex]
[latex]3x^2=3x^2[/latex] [latex]\\[/latex]
2) Symmetric Property of Equality
For any numbers [latex]a[/latex] and [latex]b[/latex], if [latex]a=b[/latex] then [latex]b=a[/latex].
[latex]\Rightarrow[/latex] If one quantity equals a second, then the second quantity equals the first.
Examples:
If [latex]1+2=3[/latex] then [latex]3=1+2[/latex].
If [latex]2y = x + y[/latex] then [latex]x + y = 2y[/latex].
If [latex]{x^2} – {y^2} = \sqrt 2[/latex] then [latex]\sqrt 2 = {x^2} – {y^2}[/latex].
3) Transitive Property of Equality
For any numbers [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex], if [latex]a=b[/latex] and [latex]b=c[/latex], then [latex]a=c[/latex].
[latex]\Rightarrow[/latex] If the first quantity is equal to the second quantity, and the second quantity is equal to the third quantity, then the first quantity must be equal to the third quantity.
Examples:
If [latex]7 + 8 = 12 + 3[/latex] and [latex]12 + 3 = 15[/latex], then [latex]7 + 8 = 15[/latex].
If [latex]3 \times 4 = 2 \times 6[/latex] and [latex]2 \times 6 = 12[/latex], then [latex]3 \times 4 = 12[/latex].
If [latex]m – n = {k^2}[/latex] and [latex]{k^2} = p + {d^3}[/latex], then [latex]m – n = p + {d^3}[/latex].
4) Addition Property of Equality
For any numbers [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex], if [latex]a=b[/latex], then [latex]a+c=b+c[/latex].
[latex]\Rightarrow[/latex] A true equation will remain true and unchanged when the same or common value is added to each side.
Example 1:
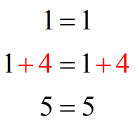
Example 2:
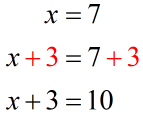
5) Subtraction Property of Equality
For any numbers [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex], if [latex]a=b[/latex], then [latex]a-c=b-c[/latex].
[latex]\Rightarrow[/latex] A true equation will remain true and unchanged when the same or common value is subtracted from each side.
Example 1:
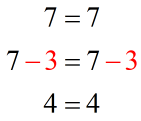
Example 2:
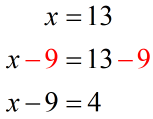
6) Multiplication Property of Equality
For any numbers [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex], if [latex]a=b[/latex], then [latex]a \times c = b \times c[/latex].
[latex]\Rightarrow[/latex] As long as the same value or quantity is multiplied on both sides of the equation, the new equation remains true and the same in meaning.
Example 1:
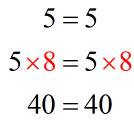
Example 2:
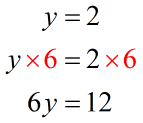
7) Division Property of Equality
For any numbers [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex], if [latex]a=b[/latex], then [latex]a \div c = b \div c[/latex].
[latex]\Rightarrow[/latex] As long as the same value or quantity is divided from both sides of the equation, the new equation remains true and the same in meaning.
Example 1:
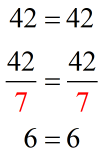
Example 2:
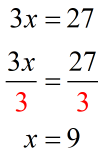
8) Substitution Property of Equality
If [latex]a=b[/latex] then [latex]b[/latex] can be substituted for [latex]a[/latex] in any expression or equation.
[latex]\Rightarrow[/latex] A quantity can be substituted or replaced by another quantity of equal or the same value in any expression or equation.
Example 1:
If [latex]x=y[/latex] and [latex]x+2[/latex], then [latex]y+2[/latex].
Example 2:
If [latex]m=5[/latex] and [latex]m-2[/latex], then [latex]5-2[/latex].
Example 3:
If [latex]x=3[/latex] and [latex]5+x=8[/latex], then [latex]5+3=8[/latex].
You may also be interested in these related math lessons or tutorials:
