How to Classify Real Numbers
The “stack of funnels” diagram below will help us easily classify any real numbers. But first, we need to describe what kinds of elements are included in each group of numbers. A funnel represents each group or set of numbers.

Description of Each Set of Real Numbers

Natural numbers (also known as counting numbers) are the numbers that we use to count. It begins with 1, then 2, 3, and so on.
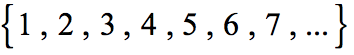

Whole numbers are a slight “upgrade” of the natural numbers because we simply add the element zero to the current set of natural numbers. Think of whole numbers as natural numbers together with zero.
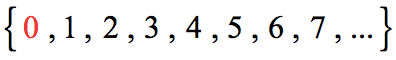

Integers include all whole numbers together with the “negatives” or opposites of the natural numbers.
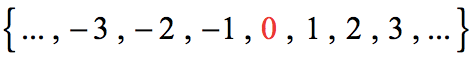

Rational numbers are numbers that can be expressed as a ratio of integers. That means if we can write a given number as a fraction where the numerator and denominator are both integers; then it is a rational number.
Symbolically, we can write a rational number as:
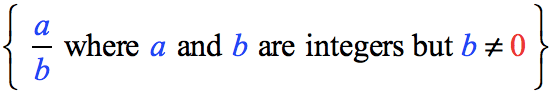
Caution: The denominator cannot equal zero.
Rational numbers can also appear in decimal form. If the decimal number either terminates or repeats, then it is possible to write it as a fraction with an integer numerator and denominator. Thus, it is rational as well.

Irrational numbers are all numbers that when written in decimal form do not repeat and do not terminate. In other words, it goes on forever indefinitely without having a definite pattern.
Real numbers include both rational and irrational numbers. Remember that under the set of rational numbers, we have the subcategories or subsets of integers, whole numbers, and natural numbers.
Classification of Real Numbers Examples
Example 1: A natural number is also a whole number. (True or False)
The set of whole numbers includes the number zero and all natural numbers. This is a true statement.
Example 2: An integer is always a whole number. (True or False)
The set of integers is composed of the number zero, natural numbers, and the “negatives” of natural numbers. That means some integers are whole numbers, but not all.
For instance, [latex] – 2[/latex] is an integer but not a whole number. This statement is false.
Example 3: Every rational number is also an integer. (True or False)
The word “every” means “all”. Can you think of a rational number that is not an integer? You only need one counterexample to show that this statement is false.
The fraction [latex]\Large{1 \over 2}[/latex] is an example of a rational number that is NOT an integer. So this statement is false.
Example 4: Every integer is a rational number. (True or False)
This is true because every integer can be written as a fraction with a denominator of [latex]1[/latex].
Example 5: Every natural number is a whole number, integer, and a rational number. (True or False)
Reviewing the descriptions above, natural numbers are found within the sets of whole numbers, integers, and rational numbers. That makes it a true statement.
We can also use the diagram of funnels above to help us answer this question. If we pour water into the “funnel of natural numbers”, the water should also flow through all the funnels below it. Thus, passing through the funnels of the whole numbers, integers, and rational numbers.
Example 6: Every whole number is a natural number, integer, and rational number. (True or False)
Using the same “funnel” analogy; if we pour some liquid into the whole numbers’ funnel, it should pass through the funnels of integers and rational numbers as it makes its way down. Since the natural numbers’ funnel is above the set of whole numbers where we started, we cannot include this funnel in the group.
It is a false statement since whole numbers belong to the sets of integers and rational numbers, but not to the set of natural numbers.
Simply put, the number zero (0) is a counterexample since it is a whole number but not a natural number. So indeed, this is a false statement.
Example 7: Classify the number zero, [latex]0[/latex].
Definitely not a natural number but it is a whole, an integer, a rational, and a real number. It may not be obvious that zero is also a rational number. However, writing it as a fraction with a nonzero denominator would clearly show that it is indeed
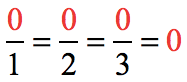
Example 8: Classify the number [latex]5[/latex].
This is a natural or counting number, a whole number, and an integer. Since we can write it as a fraction with a denominator of [latex]1[/latex], that is, [latex]\Large{5 \over 1}[/latex], it is also a rational number. And of course, this is a real number.
Example 9: Classify the number [latex]0.25[/latex].
The given decimal number terminates and so we can write it as a fraction which is a characteristic of a rational number. This number is also a real number.
[latex]\Large{0.25 = {{25} \over {100}} = {1 \over 4}}[/latex]
Example 10: Classify the number [latex]{\rm{2}}{1 \over 5}[/latex].
We can rewrite this mixed fraction as an improper fraction so that it is clear that we have a ratio of two integers.
[latex]\Large{{\rm{2}}{1 \over 5} = {{11} \over 5}}[/latex]
This number is a rational and real number.
Example 11: Classify the number [latex]{\rm{5.241879132…}}[/latex].
The decimal number is non-terminating and non-repeating that means it is an irrational number. Of course, any irrational number is also a real number.
Example 12: Classify the number [latex]1.7777…[/latex]
Since the decimal is repeating, it is a rational number. Any rational number must also be a real number.
Example 13: Classify the number [latex]\sqrt 2 [/latex].
This is an irrational number because when written in decimal form, it is non-terminating and non-repeating. This is also a real number.
Example 14: Classify the number [latex] – \sqrt {16} [/latex] .
First, we need to simplify this radical expression which gives us [latex] – \sqrt {16} = – \,4[/latex]. The number [latex] – \,4[/latex] is an integer, a rational number, and a real number.
Example 15: Classify the number [latex] – 8.123123…[/latex].
The decimal number is nonterminating, however, the string of numbers 123 after the decimal point keeps on repeating. We can rewrite the decimal number with a “bar” on top of the repeating numbers.
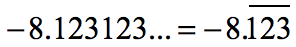
This makes it a rational number. Don’t forget that it is also a real number.
You may also be interested in these related math lessons or tutorials:
