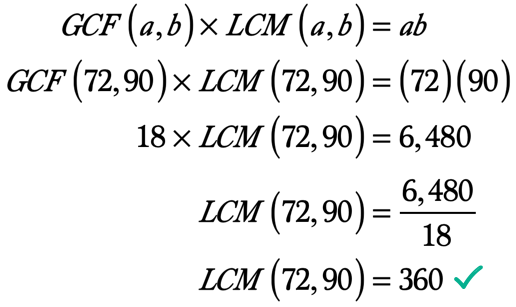The Product of the GCF and LCM of Two Integers
When you were studying how to find the GCF and LCM of two positive numbers, did you discover a very interesting relationship between the two quantities?

I did! I actually discovered it by accident when I was a young student and I thought I stumbled upon something that was “revolutionary”. I was so excited that I shared it with my teacher. But to my frustration, he looked at me in the eye and said that it was already a proven mathematical statement. I felt discouraged for a moment but I went back to my school work and pressed on.

If you haven’t encountered it yet, there is a remarkable algebraic relationship or link between the Greatest Common Factor (GCF) and the Least Common Multiple (LCM) of two numbers. In this lesson, the numbers that we want are those belonging to the set of positive integers only.
Below is the algebraic connection between the GCF and the LCM of two positive integers.
The GCF-LCM Formula
WARNING: There’s really no such thing as the “GCF-LCM Formula”. I just made up the name for ease of reference. You may call it anything you want as long as it serves its purpose.
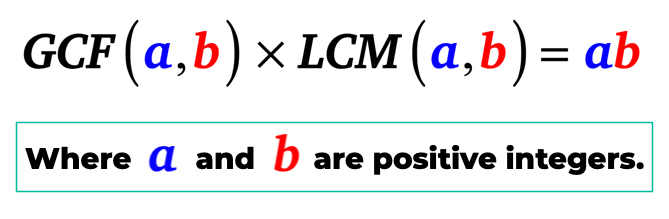
Simply put, the greatest common factor of [latex]a[/latex] and [latex]b[/latex] when multiplied to the least common multiple of [latex]a[/latex] and [latex]b[/latex] is equal to the product of [latex]a[/latex] and [latex]b[/latex]. That is, [latex]a[/latex] and [latex]b[/latex] are positive integers.
Example Problems
Example 1: The GCF of 12 and 16 is 4. What is the LCM of 12 and 16?
You can determine the LCM of [latex]12[/latex] and [latex]16[/latex] using either of the two methods below.
However, there is a much faster way. You can take advantage of the “GCF-LCM Formula” because you know the two integers and their GCF. Just plug in the values into the formula and then solve for the LCM.
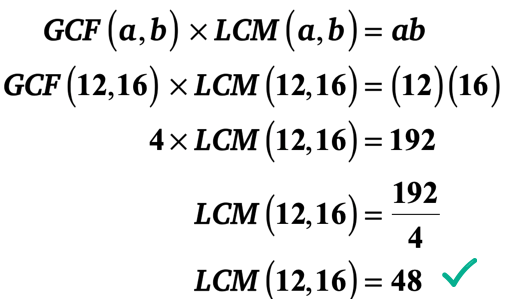
I will leave it to you to verify that the LCM of 12 and 16 is indeed 48.
Example 2: The LCM of 24 and 40 is 120. What is the GCF of 24 and 40?
This problem is the exact opposite of Example 1 because you’re given the value of the LCM instead of GCF.
So these are the information that we know. Let’s itemize them for clarity.
▶︎ LCM(24,40) = 120
▶︎ [latex]a=24[/latex] and [latex]b=40[/latex] therefore [latex]ab = \left( {24} \right)\left( {40} \right) = 960[/latex]
Note: It doesn’t really matter which numbers are [latex]a[/latex] and [latex]b[/latex]. It won’t change the outcome of the final answer. However, it’s a good practice to standardize your solution. I suggest that you let [latex]a[/latex] be the smaller integer while [latex]b[/latex] be the larger integer.
Let’s substitute the known values into the formula then solve for the GCF of 24 and 40.
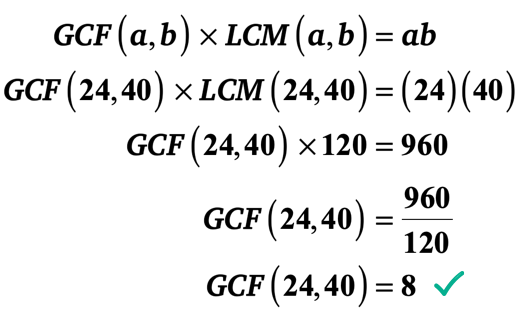
Example 3: Find the GCF of 20 and 25 by first calculating the LCM of 20 and 25.
This problem will be a bit different from examples #1 and #2. You will need to calculate first the Least Common Multiple (LCM) of 20 and 25. After that, you can solve for the Greatest Common Factor (GCF) of 20 and 25 by using the GCF-LCM Formula.
So here we go! To find the LCM of 20 and 25, we will write the first few multiples of 20 and 25. The very first common multiple that shows up will be our LCM.
Multiples of 20: 20, 40, 60, 80, 100, 120
Multiples of 25: 25, 50, 75, 100, 125, 150
Since the number [latex]100[/latex] shows up as the first common multiple of [latex]20[/latex] and [latex]25[/latex], then we can claim that the LCM of [latex]20[/latex] and [latex]25[/latex] is [latex]100[/latex].
We now have all the information to use the formula. Below are the values that we are going to substitute into the formula to solve for the LCM of 20 and 25.
◉ The product of [latex]a[/latex] and [latex]b[/latex] → [latex]ab = \left( {20} \right)\left( {25} \right) = 500[/latex]
◉ The LCM of 20 and 25 → [latex]LCM\left( {20,25} \right) = 100[/latex]
Here’s the calculation to solve for the GCF of 20 and 25:
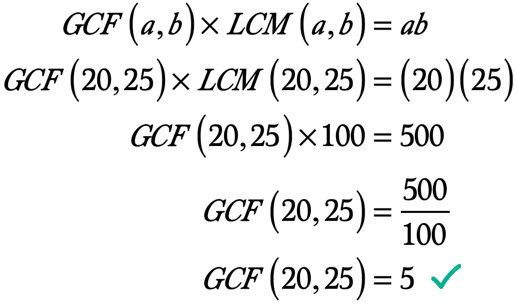
Example 4: Find the LCM of 63 and 84 by first calculating the GCF of 63 and 84.
This problem is very similar to example #3. The only difference is that you will calculate first the GCF instead of the LCM, as instructed by the problem itself.
Let’s find all the factors of 63 and 84. You can use the “rainbow method” technique to factor the given integers.
Notice that the largest or highest common factor between the two lists is [latex]21[/latex].
Factors of 63: 1, 3, 7, 9, 21, 63
Factors of 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Therefore, the Greatest Common Factor of 63 and 84 is 21. Thus, [latex]GCF\left( {63,84} \right) = 21[/latex].
Since [latex]ab = \left( {63} \right)\left( {84} \right) = 5,292[/latex] and [latex]GCF\left( {63,84} \right) = 21[/latex], we can now plug in these values into the formula then solve for the LCM of 63 and 84.
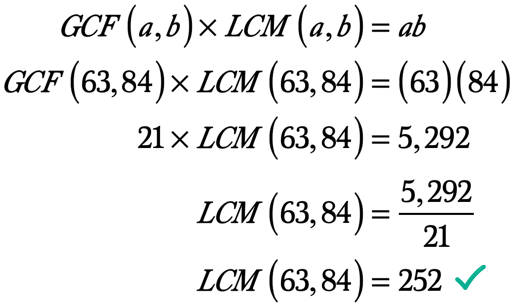
Example 5: Find the LCM of 72 and 90 using the GCF-LCM Formula.
As we already know, we can find the LCM of two integers with the value of its GCF using the GCF-LCM Formula.
Listing both the factors of 72 and 90, we have:
All factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
All factors of 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
When we compare the lists of factors, we see that 18 is the factor that is common to both but has the largest or greatest in value. It means the GCF of 72 and 90 is 18, that is, [latex]GCF\left( {72,90} \right) = 18[/latex].
We are now ready to substitute the values below in the formula.
❖ [latex]ab = \left( {72} \right)\left( {90} \right) = 6,480[/latex]
❖ [latex]GCF\left( {72,90} \right) = 18[/latex]
Here’s the calculation to find the LCM given that we know already the GCF of the two integers and their product.