Find All Factors of a Number using the Rainbow Method
There are a few ways how to find all the factors of a number. However, I think the easiest and the most intuitive way is by using the so-called rainbow method. Once you get the basic methodology of this technique, more likely, you will always remember it. Plus, the visual aspect of the rainbow method is very effective to keep track of all possible factors of a number.
How to Find All Factors of a Number using the Rainbow Method
- First, write down the first nine elements of the set of counting numbers.
- Once you have the number on which you want to find all the factors, begin by dividing the number by [latex]1[/latex] which is the first number on your list. Your
first factor pair will then be [latex]1[/latex] and the number itself. Don’t be alarmed as this is always the case. You will then write the first two factors with enough space between them.
- Next, move on to the next number on the list, which is [latex]2[/latex], to test if you can also get a factor pair.
If you can, write the new factor pairs inside the first factor pair giving it enough space in the middle as well.
If can’t get a factor pair, move on to the next number on your list.
- You will repeat this process until you have found all the factors of the given number.
The best way to learn this rainbow method in finding all the factors of a given number is to go over a few examples.
Examples of Finding All Factors of a Number using the Rainbow Method
Example 1: Find all the factors of [latex]18[/latex] using the Rainbow Method.
We’ll start by listing the first nine counting numbers.
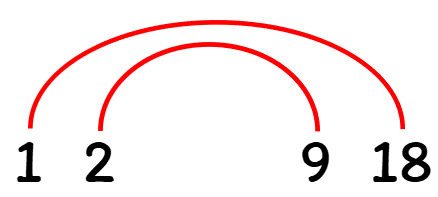
Now, dividing [latex]18[/latex] by the first number on the list, which is [latex]1[/latex], we have [latex]18 \div 1 = 18[/latex]. Therefore, our first factor pair is [latex]1[/latex] and [latex]18[/latex].
We will write this first factor pair with enough space in between.

This time, let’s divide [latex]18[/latex] by the second number on the list which is [latex]2[/latex]. Does it give us a factor pair? The answer is yes, because [latex]18 \div 2 = 9[/latex]. So our next factor pair is [latex]2[/latex] and [latex]9[/latex]. Let’s write this factor pair on our rainbow diagram.
Moving on to the next number on the list, we ask ourselves again if [latex]18[/latex] is divisible by [latex]3[/latex]. Sure it is! We have [latex]18 \div 3 = 6[/latex].
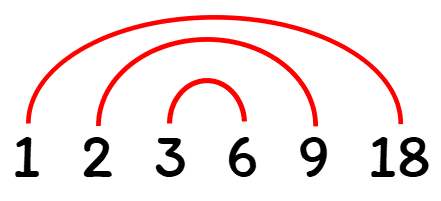
So after [latex]3[/latex], we test the next number which is [latex]4[/latex]. Is [latex]18[/latex] divisible by [latex]4[/latex]? The answer is no. Therefore, we cannot write a factor pair with [latex]4[/latex] as one of the factors. We are not done yet though because we have to go through all the numbers on the list until we hit a stopping point.
Since we cannot make a factor pair with [latex]4[/latex], we move on to [latex]5[/latex]. Unfortunately, [latex]18[/latex] is also not divisible by [latex]5[/latex] so the next number to test is [latex]6[/latex]. But, notice that we already have a factor pair with [latex]6[/latex] in our rainbow diagram. This is when we stop.
We can now list all the possible factors of [latex]18[/latex]:
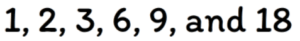
Example 2: Find all the factors of the number [latex]42[/latex] using the Rainbow Method.
Always have a list of the counting numbers nearby, at least from [latex]1[/latex] to [latex]9[/latex].
We should already know that any whole number is divisible by [latex]1[/latex] which means our

The next counting number to check is [latex]3[/latex]. Since [latex]42 \div 3 = 14[/latex] that means our next factor pair is [latex]3[/latex] and [latex]14[/latex]. I will leave it to you to check that [latex]4[/latex] and [latex]5[/latex] do not evenly divide [latex]42[/latex]. This is our updated rainbow diagram of factor pairs.
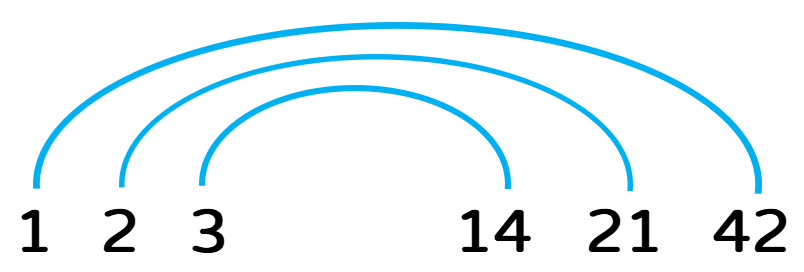
Moving on, we know that [latex]6 \times 7 = 42[/latex], therefore, we can include this factor pair in our diagram.

After [latex]6[/latex], the next number to check is [latex]7[/latex]. However, [latex]7[/latex] is already one of the factors as shown above so we stop here.
These are all the factors of the number [latex]42[/latex]:
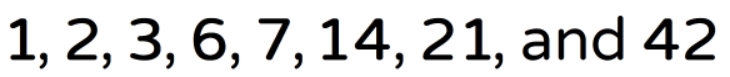
Example 3: Find all the factors of the whole number [latex]60[/latex] using the Rainbow Method.
This one is actually very easy. Keep in mind the first nine counting numbers. Let’s go through it together. We know that [latex]1[/latex] evenly divides [latex]60[/latex]. How about [latex]2[/latex] and [latex]3[/latex] ? It is crystal clear that both [latex]2[/latex] and [latex]3[/latex] evenly divides [latex]60[/latex]. In addition, by doing a quick mental calculation, the next counting numbers which are [latex]4[/latex], [latex]5[/latex], and [latex]6[/latex] can divide [latex]60[/latex] without remainders. So for a recap, the counting numbers from [latex]1[/latex] to [latex]6[/latex] produce factor pairs. Again, I will leave it to you to verify that [latex]60[/latex] is not divisible by [latex]7[/latex], [latex]8[/latex], or [latex]9[/latex]. You might say that [latex]10[/latex] divides [latex]60[/latex] which is true. But [latex]10[/latex] is already covered by the factor pair [latex]6[/latex] and [latex]10[/latex]. Below is the complete rainbow diagram of [latex]60[/latex]:
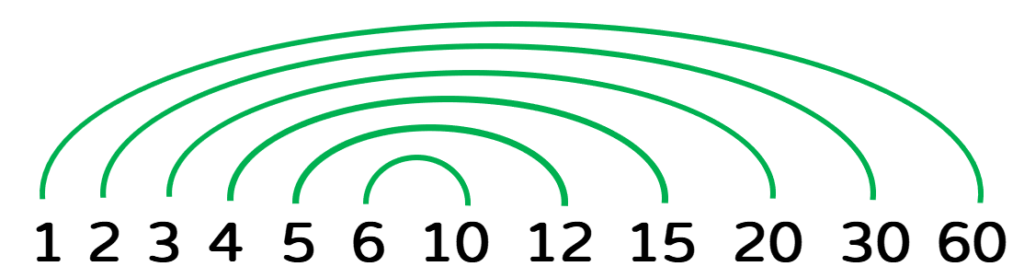
The following is a list of all the factors of [latex]60[/latex]:
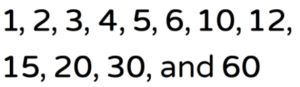
You may also be interested in these related math lessons or tutorials:
