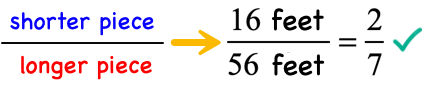Basic Proportions
Suppose there are two ratios [latex]a:b[/latex] and [latex]c:d[/latex]. They can be written as fractions [latex]\Large{a \over b}[/latex] and [latex]\Large{c \over d}[/latex], respectively. Now, if we set these two ratios equal to each other then it becomes a proportion.
Ways to Write a Proportion
Proportion is a statement showing that two ratios are equal. There are two ways to write a proportion:


Both can be read as “[latex]a[/latex] is to [latex]b[/latex] as [latex]c[/latex] is to [latex]d[/latex]”.
Next, let’s identify the parts of a proportion. We need this concept in order to solve problems later on.
- COLON FORM

In colon form, the extremes are the two outermost values, while the means are the two innermost values.
- FRACTION FORM (Standard Form)
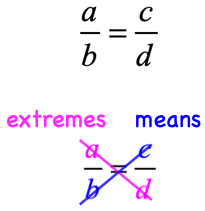
In a fraction form, the extremes are the values hit by a diagonal drawn from top left to bottom right, while the means are the values hit by a diagonal drawn from the bottom left to top right.
After getting familiar with the definition and parts of a proportion, we can now talk about the properties of proportions. These are two useful properties that can be used to solve problems.
Properties of Proportions
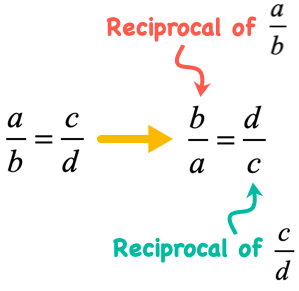
1) Reciprocal Property
If two ratios are equal, then their reciprocals must also be equal as long as they exist.
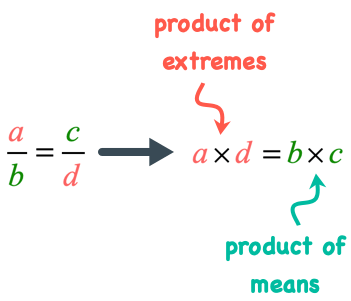
2) Cross Product Property
The product of the extremes is equal to the product of the means.
Examples of How to Apply the Concept of Proportions
Example 1: Show that the proportion below is true.
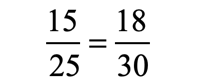
In order for a proportion to be true, the fractions on both sides of the equations must be reduced to the same value. The fraction on the left side of the equation has a greatest common divisor of [latex]5[/latex]. While the fraction on the right has a greatest common divisor of [latex]6[/latex].
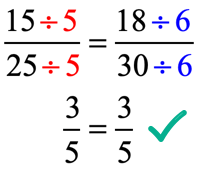
Since the two fractions on both sides are equal after reducing to lowest terms, we can claim that the given proportion is true!
Example 2: Show that the proportion below is true.
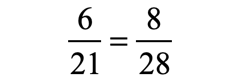
We can also show if a proportion is true using the Cross Product Property. Simply put, if the product of their extremes (outer values) equals the product of means (inner values) then the proportion is true.
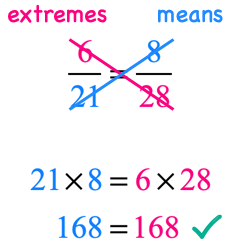
This shows that the given proportion is true!
Example 3: Solve the proportion below.
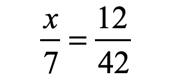
This problem is a proportion with an unknown value. Our goal is to find the value of “[latex]x[/latex]” that could make the proportion a true statement. We can easily solve this using the Cross Product Property.
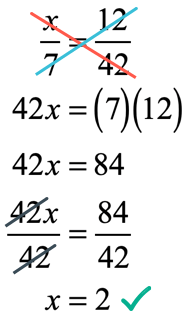
You may back substitute [latex]x = 2[/latex] into the original proportion and verify that it is indeed the correct answer.
Example 4: Solve the proportion below.
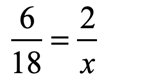
The only difference of this problem from example #3 is that the unknown variable “[latex]x[/latex]” is found in the denominator. Solving this proportion is as easy as applying the Cross Product Property and then solving the simple equation that comes out of it.
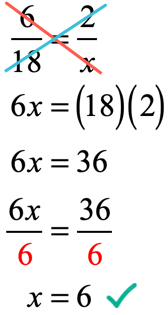
Alternatively, you may first apply the Reciprocal Property to move the variable “[latex]x[/latex]” from the bottom to the top before using the Cross Product Property. The answer should come out the same.
Example 5: Solve the proportion below.
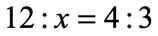
This is another type of problem that you may encounter when solving proportions. The format of the proportion is using a colon instead of a fraction. To work this out, we need to rewrite the proportion in fractional form, and then solve this as usual.
Since [latex]a:b = c:d[/latex] can be written as [latex]\Large{a \over b} = {c \over d}[/latex], then our original problem becomes [latex]\Large{{12} \over x} = {4 \over 3}[/latex].
Let’s go ahead and solve this…
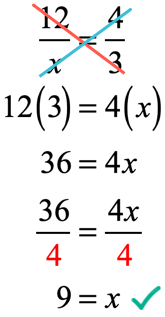
Substitute [latex]x = 9[/latex] back to the original proportion to verify your answer.
Example 6: The exchange rate between the US Dollar and the Indian Rupee is [latex]2[/latex] to [latex]106[/latex]. At this rate, how much US Dollars would you have if you exchanged [latex]901[/latex] Indian Rupees?
What we want is to set up a proportion that we can solve. We can do this two ways. One way is to place the dollar values in the numerators while the rupees in the denominators of the proportion. And the other way is to swap their locations. Either of the setups should give us the same answer.
For this exercise, we will put the dollar information on top.

Solve the unknown value of “[latex]x[/latex]” to get the required dollar value.
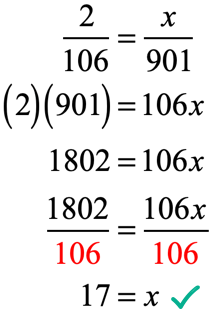
That means at the time of the exchange, [latex]17[/latex] US Dollars is equivalent to [latex]901[/latex] Indian Rupees.
NOTE: The next example is a
Example 7: You want to cut a block of wood with a length of [latex]72[/latex] feet into two pieces such that the ratio of the shorter to the longer piece is [latex]2[/latex] to [latex]7[/latex]. What are their lengths?
Let “[latex]x[/latex]” be the length of the shorter piece. That means “[latex]72 – x[/latex]” will be the longer piece. See the diagram below.
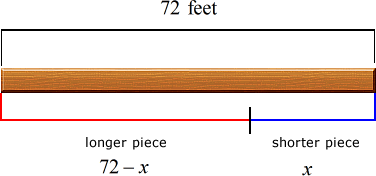
It is given that the ratio of the shorter to the longer piece is [latex]2:7[/latex]. Using all this information, we can now set up the proportion to solve for the lengths of both short and longer pieces.

Solving the proportion above using the Cross Product Property of Proportionality…
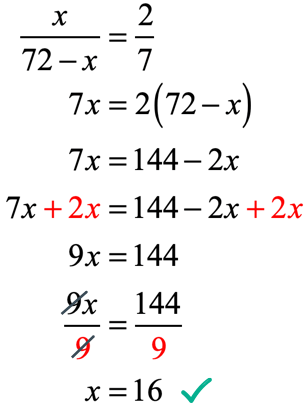
Since the shorter piece is [latex]x = 16[/latex] feet, that means the longer piece is [latex]72 – x = 72 – 16 = 56[/latex] feet.
To perform a check, we were told in the problem that the ratio of the shorter piece to longer piece is [latex]2[/latex] to [latex]7[/latex]. Notice that when we reduce the fraction [latex]\Large{{16} \over {56}}[/latex] to the lowest term, we will get the desired ratio.