Adding and Subtracting Numbers using the Number Line

Adding numbers on a number line is an interesting way to see how numbers are added visually.

I. Steps on How to Add Numbers on the Number Line

here is a diagram of a number with zero at the center, integers 1 to 7 on the right side, and integers -1 to -7 on the left side. there are notes under the number line that to add a positive number, you move some units to the right of the number line while to add a negative number means you move some units to the left of the number line.

As indicated in the diagram:

To add a positive number means that we move the point to the right of the number line.

Similarly, to add a negative number implies that we move the point to the left of the number line.

Examples of Adding Numbers on the Number Line

Example 1: Simplify by adding the numbers, 2 + 4.

The first step is to locate the first number which is 2 on the number line.

the number two or 2 is represented as a dot on a number line

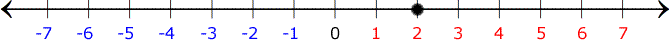
Adding 4 means we have to move the point, 4 units to the right.

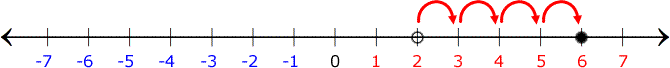
the original number two is moved 4 units to the right of the number line to indicate addition

After doing so, we end up at 6. Therefore, 2 + 4 = 6.

Example 2: Simplify by adding the numbers, 3 + (–5).

Locate the first point, 3, on the number line.

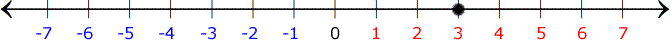
the number three or 3 is represented as a dot on the number line. since +3 is positive, it is positioned at 3 units to the right of the center which is zero.

Now, we are going to add -5 which tells us to move the point, 5 units going to the left.

the original positive 3 is moved 5 units to the left ending at negative two or -2 on the number line. this means that 5 is subtracted from positive three or +3. observe that when adding negative numbers, you move the number to the left.

We arrive at −2. That’s why 3 + (–5) = –2.

Example 3: Simplify by adding the numbers, â€“6 + 5.

Find where −6 is on the number line. To add 5, the original point will be moved 5 units to the right.

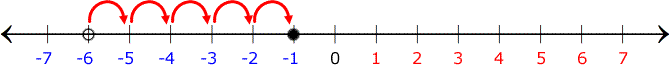
the original number six or -6 is added by 5 units. it means that -6 will move 5 units to the right of the number line which ends at number negative one or -1.

This gives us â€“6 + 5 = –1.

Example 4: Simplify by adding the numbers, â€“1 + (–6).

This time around, we are adding two negative numbers. To start, locate the first number which is −1. Then, add -6 to it which means moving the existing point, 6 units to the left of the number line.

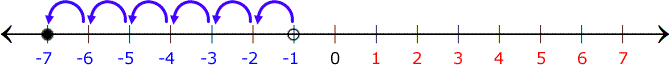
-1 is relocated 6 units to the left of the number line which ends at -7

Therefore, we have â€“1 + (–6) = –7.

II. Steps on how to Subtract Numbers by Converting to Addition on the Number Line

The process of subtracting numbers is very similar to adding numbers with a very slight “twist”. The trick is to change the operation from subtraction to addition, then switch the sign of the number that follows it.

In other words, to “subtract” means to “add its opposite“.

Examples of Subtracting Numbers on the Number Line

Example 5: Simplify by subtracting the numbers, 5 − (+6).

As mentioned before, subtraction is just addition. After changing the operation from subtraction to addition, we must take the opposite sign of the number following it. That means, we can rewrite the problem as

5 − (+6) â†’ 5 + (–6)

Since we already know how to add, this problem should be a breeze! We locate the first number which is 5 and then move it 6 units to the left.

positive five or +5 is moved 6 units to the left of the number line. it lands on the number negative one or -1.

This gives us the answer of 5 − (+6) = 5 + (–6) = –1.

Example 6: Simplify by subtracting the numbers, â€“4 − (–7).

This is an example where we subtract two negative numbers. Let’s transform this subtraction into an addition problem. Remember always add to its opposite.

–4 − (–7) â†’ â€“4 + (+7)

Start by locating the first number, −4, and then move it 7 units to the right of the number line.

the integer negative four or -4 is moved 7 units to the right of the number line which ends at positive three or +3

We arrived at 3. That’s why –4 − (–7) = –4 + (+7) = 3.