How to Solve Compound Inequalities
When solving compound inequalities, we are going to deal with two general cases or types.
- The first case involves solving two linear inequalities joined by the word “and”. The word “and” is also known as a conjunction. The solution of an “and” compound inequality is the set of all values of x that satisfy both of the two inequalities. In other words, you want a solution set that works with both inequalities. The other way of saying it is that the solution set of the “and” compound inequality is the intersection, represented by the symbol [latex]\Large{\color{red} \cap}[/latex], of the two inequalities.
- As for the second case, it involves solving two linear inequalities joined by the word “or”. The solution of an “or” compound inequality is the set of all [latex]x[/latex] that satisfy either of the two inequalities or at times satisfies the two at the same time. In other words, you want a solution that works on at least one inequality. The other way of saying it is that the solution set of the “or” compound inequality is the union, represented by the symbol [latex]\Large{\color{red} \cup }[/latex], of the two inequalities.
In both cases, the solutions of compound inequalities can be expressed as graphs on the number line and also as interval notations.
I suggest that you first graph the solutions of the two inequalities on the number line before writing the solution of the compound inequality in the interval notation. By having a visual representation of how the two inequalities behave on the number line, it is much easier to write its corresponding interval notation.
We will also go over some examples where the compound inequality has no solution or infinite solution.
Somewhere in our examples, we will discuss an “and” compound inequality case which can be condensed into a single inequality with three parts: left side, middle part, and right side. An example would be [latex] – 1 \le x \le 3[/latex] which is derived from [latex] -1 \le x[/latex] and [latex]x \le 3[/latex]. By writing it in this form, it can allow us to solve the compound inequality much quicker.
The “AND” Compound Inequalities
Solve the compound “and” inequality by solving each of the two inequalities separately then examine or consider their solutions altogether. For the “and” case, we want to find all the numbers or values that can make both the two inequalities true.
Example 1: Solve the compound inequality [latex]x – 1 > 1[/latex] and [latex]27 \ge 2x – 1[/latex]. Graph the solutions on the number line. Then, write your solutions in interval notation.
STEP 1. Solve each inequality.
- First inequality: [latex]x – 1 > 1[/latex]
Add [latex]1[/latex] to both sides of the inequality.
[latex]x – 1 > 1[/latex]
[latex]x – 1+1 > 1+1[/latex]
[latex]\color{red}x > 2[/latex]
- Second inequality: [latex]27 \ge 2x – 1[/latex]
Add both sides of the inequality by [latex]1[/latex] then divide by [latex]2[/latex]. Finally, make sure that the variable is on the left side. When you swap location, in this case, the variable [latex]x[/latex] will move from right to left. The relative orientation of the inequality symbol should remain the same to keep the meaning unchanged. One way to think about it is that the “mouth” of the inequality symbol is opening towards the number [latex]14[/latex]. So when you swap, the “mouth” of the inequality must still be pointing towards [latex]14[/latex].
[latex]27 \ge 2x – 1[/latex]
[latex]27 + 1 \ge 2x – 1 + 1[/latex]
[latex]8 \ge 2x [/latex]
[latex]{\Large{{{28} \over 2}}} \ge {\Large{{{2x} \over 2}}}[/latex]
[latex]14 \ge x[/latex]
[latex]\color{red}x \le 14[/latex]
The solutions are given by [latex]\color{red}x > 2[/latex] and [latex]\color{red}x \le 14[/latex].
STEP 2. Graph the solutions on the number line.
For [latex]\color{red}x > 2[/latex], the point [latex]2[/latex] is not included as part of the solutions since [latex]x > 2[/latex] means all numbers greater than [latex]2[/latex]. In addition, it does not have any conditions of equality that’s why we must exclude the number [latex]2[/latex]. So we will put an open circle over [latex]2[/latex] to indicate that it is not a solution. The solutions are all numbers greater than [latex]2[/latex], thus we draw an arrow to the right of [latex]2[/latex].
For [latex]\color{red}x \le 14[/latex], we read it as “[latex]x[/latex] is less than or equal to [latex]14[/latex]”. Notice there is a condition of equality, therefore the number [latex]14[/latex] is part of the solution so we will put a closed circle over it. All numbers to the left of [latex]14[/latex] are also solutions so we will draw an arrow pointing to the left of it.
The final solutions will be the intersection or overlap of the two inequalities: [latex]\color{red}x > 2[/latex] and [latex]\color{red}x \le 14[/latex]. Notice that all the numbers between [latex]2[/latex] and [latex]14[/latex] intersect so they are part of the final solutions of the “and” compound inequality. They also intersect at the number [latex]14[/latex] so we add it in the solution set. However, they do not intersect at point [latex]2[/latex], thus we drop it off as part of the solutions. We have just figured out the complete solution set of the given compound inequality.
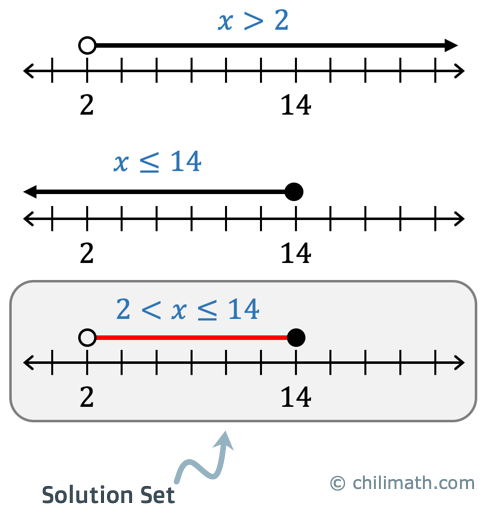
STEP 3. Write the solutions in interval notation.
Observe that all numbers between [latex]2[/latex] and [latex]14[/latex] are part of the solutions. In addition, the number [latex]2[/latex] is excluded because it is with an open circle while [latex]14[/latex] is included because it is covered with a closed circle. Now, we use a rounded bracket or parenthesis if it is excluded (2 is excluded), and use a square bracket if included (14 is included).
[latex]\Large{\left( {2,14} \right]}[/latex]
It is read as “all the numbers greater than [latex]2[/latex] but less than or equal to [latex]14[/latex]”.

Remember: This type of interval is also known as half-closed or half-open interval because one of the two endpoints is included but the other is not.
Example 2: Solve the compound inequality [latex]2 + 3x > – 10[/latex] and [latex]2\left( {x – 1} \right) < x + 4[/latex]. Graph the solution set on the number line. Then, write the solution set in the interval notation.
STEP 1. Solve each inequality.
- First inequality: [latex]2 + 3x > – 10[/latex]
Subtract both sides of the inequality by [latex]2[/latex]. Then divide both sides by [latex]3[/latex].
[latex]2 + 3x > – 10[/latex]
[latex]2 – 2 + 3x > – 10 – 2[/latex]
[latex]3x > – 12[/latex]
[latex]{\Large{{{3x} \over 3}}} > {\Large{{{ – 12} \over 3}}}[/latex]
[latex]\color{red}x > – \,4[/latex]
- Second Inequality: [latex]2\left( {x – 1} \right) < x + 4[/latex]
Distribute the [latex]2[/latex] to the binomial inside the parenthesis. Add [latex]2[/latex] on both sides by of the inequality. Then subtract both sides by [latex]x[/latex].
[latex]2\left( {x – 1} \right) < x + 4[/latex]
[latex]2x – 2 < x + 4[/latex]
[latex]2x – 2 + 2 < x + 4 + 2[/latex]
[latex]2x < x + 6[/latex]
[latex]2x – x < x – x + 6[/latex]
[latex]\color{red}x < 6[/latex]
The solutions are given by [latex]\color{red}x > – \,4[/latex] and [latex]\color{red}x < 6[/latex].
STEP 2. Graph the solution set on the number line.
A strict inequality is a type of inequality that is either absolutely greater than a number, [latex]x>a[/latex], or absolutely less than a number, [latex]x<a[/latex]. Notice that strict inequality does not contain any equality component.
On the other hand, the inequality symbol [latex]x \ge a[/latex] which is read as “[latex]x[/latex] is greater than or equal to [latex]a[/latex] and the inequality symbol [latex]x \le a[/latex] which is read as “[latex]x[/latex] is less than or equal to [latex]a[/latex]” are both non-strict inequalities because they have the equality conditions.
The inequality [latex]\color{red}x > – \,4[/latex] is a strict inequality therefore we will put an open circle over [latex]-4[/latex] as it is not part of the solutions, and draw an arrow to the right. Similarly, [latex]\color{red}x < 6[/latex] is a strict inequality thus we will put an open circle over [latex]6[/latex] , and draw an arrow to the left.
The final solution set will be the intersection of [latex]\color{red}x > – \,4[/latex] and [latex]\color{red}x < 6[/latex] which are all the numbers between [latex]-4[/latex] and [latex]6[/latex] but excluding the endpoints [latex]-4[/latex] and [latex]6[/latex].
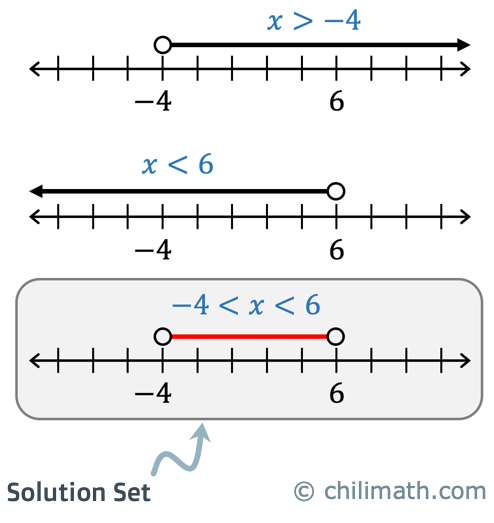
STEP 3. Write the solutions in interval notation.
We will use rounded brackets or parentheses on both sides to signify that both endpoints are excluded from the solution set.
[latex]\Large{\left( {-4,6} \right)}[/latex]
It is read as “all the numbers greater than [latex]-4[/latex] but less than [latex]6[/latex]”.

Remember: This type of interval is also known as an open interval because the two endpoints are excluded in the solution set. That is, they are NOT part of the solutions.
Example 3: Solve the compound inequality [latex]5 – 3\left( {x – 2} \right) \le x – \left( { – 2x + 13} \right)[/latex] and [latex]5 – \left( {x + 1} \right) \le 2\left( {7 – x} \right) + 1[/latex]. Graph the solution set then write its solutions in the interval notation.
STEP 1: Solve each inequality.
- First inequality: [latex]5 – 3\left( {x – 2} \right) \le x – \left( { – 2x + 13} \right)[/latex]
Get rid of the parenthesis on each side of the inequality using the Distributive Property of Multiplication over Addition. Add [latex]5[/latex] and [latex]6[/latex] on the left. Subtract both sides by [latex]11[/latex]. Subtract both sides by [latex]3x[/latex]. To solve [latex]x[/latex], divide both sides by [latex]-6[/latex]. Since we divide each side by a negative number, we will switch the direction of the inequality. That is, “from less than or equal to” to “greater than or equal to”.
[latex]5 – 3\left( {x – 2} \right) \le x – \left( { – 2x + 13} \right)[/latex]
[latex]5 – 3x + 6 \le x + 2x – 13 [/latex]
[latex]- 3x + 11 \le 3x – 13 [/latex]
[latex]- 3x + 11 – 11 \le 3x – 13 – 11[/latex]
[latex]- 3x \le 3x – 24 [/latex]
[latex]- 3x -3x \le 3x – 3x+24 [/latex]
[latex]- 6x \le-24[/latex]
[latex]{\Large{{{ – 6x} \over { – 6}}}} \le {\Large{{{ – 24} \over { – 6}}}}[/latex]
[latex]\color{red}x \ge 4[/latex]
- Second Inequality: [latex]5 – \left( {x + 1} \right) \le 2\left( {7 – x} \right) + 1[/latex]
Eliminate the parentheses using the Distributive Property of Multiplication over Addition. Subtract [latex]5[/latex] by [latex]1[/latex] on the left side. Subtract [latex]4[/latex] to both sides of the inequality. Then add [latex]2x[/latex] to both sides to finish it off.
[latex]5 – \left( {x + 1} \right) \le 2\left( {7 – x} \right) + 1[/latex]
[latex] 5 – x – 1 \le 14 – 2x + 1 [/latex]
[latex]4 – x \le 15 – 2x [/latex]
[latex]4 – 4 – x \le 15 – 4 – 2x [/latex]
[latex] – x \le 11 – 2x [/latex]
[latex] – x + 2x \le 11 – 2x + 2x[/latex]
[latex]\color{red}x \le 11 [/latex]
The solutions are given by [latex]\color{red}x \ge 4[/latex] and [latex]\color{red}x \le 11 [/latex].
STEP 2. Graph the solution set on the number line.
For [latex]\color{red}x \ge 4[/latex], we will shade the circle above [latex]4[/latex] to show that it is included in the solutions because the inequality has a condition of equality, that is, “greater than or equal to”. The arrow points to the right of [latex]4[/latex] because it has a component of “greater than”.
For [latex]\color{red}x \le 11 [/latex], we will also shade the circle above [latex]11[/latex] to indicate that is it is part of the solution set since the inequality has a condition of equality, that is, “less than or equal to”. The arrow points to the left of [latex]11[/latex] because it is of the case of less than.
As for the final solution set, we find all the points where the two inequalities intersect. Obviously, they intersect between [latex]4[/latex] and [latex]11[/latex]. More so, they also overlap at the endpoints. Therefore, the final solution set contains all the points between the endpoints [latex]4[/latex] and [latex]11[/latex] and including the endpoints.
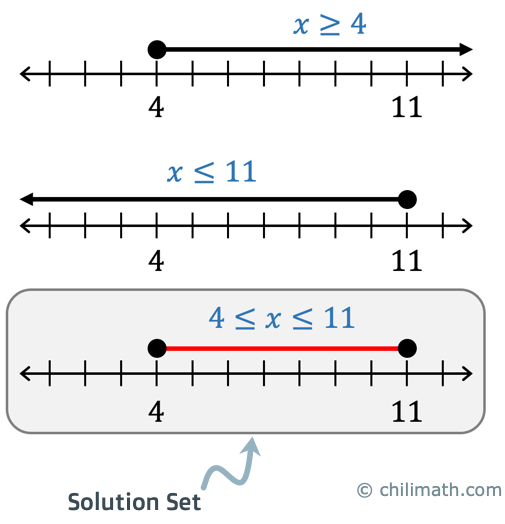
STEP 3. Write the solution set in interval notation.
We will use square brackets on both sides to signify that both endpoints are included in the solution set.
[latex]\Large{\left[ {4,11} \right]}[/latex]
It is read as “all numbers greater than or equal to [latex]4[/latex] but less than or equal to [latex]11[/latex]”.

Remember: This type of interval is also known as a closed interval because the two endpoints are included in the solution set. That is, they are part of the solutions.
Example 4: Solve the compound inequality [latex]3x – 2\left( {1 – x} \right) < x – 6[/latex] and [latex] 10 – x < x + 2[/latex]. Graph the solution set then write its solutions in the interval notation.
STEP 1. Solve each inequality.
- First inequality: [latex]3x – 2\left( {1 – x} \right) < x – 6[/latex]
Distribute the [latex]-2[/latex] into the binomial [latex]1-x[/latex] on the left side of the inequality to remove the parenthesis. Add [latex]3x[/latex] and [latex]2x[/latex] on the left side as well. Add [latex]2[/latex] to both sides of the inequality. Subtract [latex]x[/latex] on both sides. Finally, divide both sides of the inequality by [latex]4[/latex].
[latex]3x – 2\left( {1 – x} \right) < x – 6[/latex]
[latex]3x – 2 + 2x < x – 6 [/latex]
[latex]5x – 2 < x – 6 [/latex]
[latex]5x – 2 + 2 < x – 6 + 2 [/latex]
[latex]5x < x – 4 [/latex]
[latex]5x – x < x – x – 4 [/latex]
[latex]4x < – 4 [/latex]
[latex]{\Large{{{4x} \over 4}}} < {\Large{{{ – 4} \over 4}}} [/latex]
[latex]\color{red}x <- 1 [/latex]
- Second inequality: [latex] 10 – x < x + 2[/latex]
Subtract both sides of the inequality by [latex]10[/latex]. Then, subtract it also on both sides by [latex]x[/latex]. Finally, divide each side by [latex]-2[/latex]. Since we are dividing by a negative number, we must flip or switch the direction of the inequality symbol. In this case, from less than to greater than.
[latex]10 – x < x + 2 [/latex]
[latex]10 – 10 – x < x + 2 – 10 [/latex]
[latex]- x < x – 8 [/latex]
[latex]- x – x < x – x – 8 [/latex]
[latex]- 2x < – 8 [/latex]
[latex]{\Large{{{ – 2x} \over { – 2}}}} > {\Large{{{ – 8} \over { – 2}}}} [/latex]
[latex]\color{red} x > 4[/latex]
Observe that the solutions of the two inequalities [latex]\color{red}x <- 1 [/latex] and [latex]\color{red} x > 4[/latex] do not intersect, and thus the compound inequality has no solution.
It is more obvious that they don’t overlap if we look at their graphs on the number line.
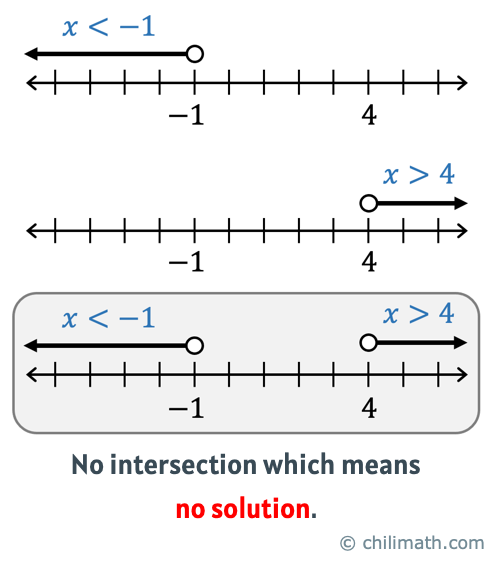
Example 5: Solve the compound inequality [latex] – 5 < 3x + 7 \le 22[/latex]. Graph the solution set then write its solutions in the interval notation.
This hybrid-looking inequality which is comprised of two inequality symbols and three parts is actually a combination of two inequalities joined together by an “AND” conjunction.
We can separate this compound inequality into two inequalities with an “AND” connector and then solve them as usual. This is how it looks if we break the compound inequality into two simpler inequalities.
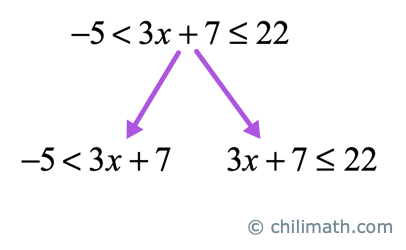
However, there is no need to separate it into two inequalities. We can solve the compound inequality as it stands. In fact, I like it the way it is because it is much easier to solve.
The goal is to isolate the variable of the middle part. To keep everything balanced, whatever we do on the middle part, we must do the same on the left side and the right side. When it is done properly, the answer should come out nicely!
Here we go. Let’s work it out!
STEP 1: Solve the compound inequality.
To solve for [latex]x[/latex], we subtract the middle by [latex]7[/latex] which means we have to do the same with the left and right side of the compound inequality. Finally, to isolate [latex]x[/latex], we divide the middle by [latex]3[/latex] which we will do the same to the left and right.
[latex]- 5 < 3x + 7 \le 22[/latex]
[latex]- 5 {\color{red}- 7} < 3x + 7{\color{red} – 7} \le 22{\color{red} – 7} [/latex]
[latex]- 12 < 3x \le 15[/latex]
[latex]{\Large{{{ – 15} \over {\color{red}3}}}} < {\Large{{{3x} \over {\color{red}3}}}} \le {\Large{{{15} \over {\color{red}3}}}}[/latex]
[latex]- 4 < x \le 5[/latex]
The solutions are given by [latex]- 4 < x \le 5[/latex].
STEP 2. Graph the solution set on the number line.
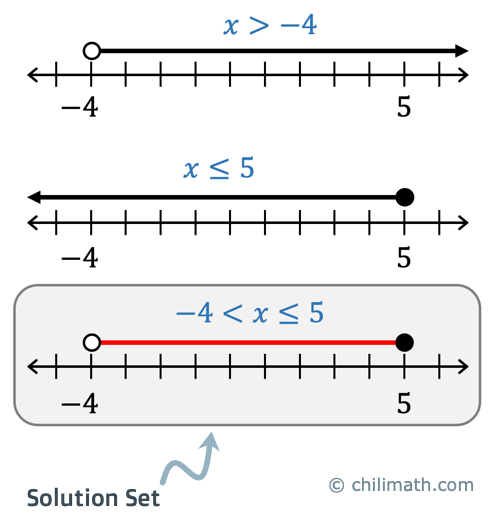
STEP 3. Write the solutions in interval notation.
[latex]\Large{\left( {-4,5} \right]}[/latex]
It is read as “all numbers greater than [latex]-4[/latex] but less than or equal to [latex]5[/latex]”.
The “OR” Compound Inequalities
Solve the compound “or” inequality by solving each of the two inequalities separately. For the “or” case, we want to find all the numbers that can make at least one of the two inequalities to be true.

Example 6: Solve the compound inequality [latex]2x – 5 > 3x + 2[/latex] or [latex]x – 1 < 2x – 5[/latex]. Graph the solutions on the number line. Then, write your solutions in interval notation.
STEP 1. Solve each inequality.
Add [latex]5[/latex] to both sides of the inequality. Then subtract [latex]3x[/latex] on both sides. Finally, divide [latex]-1[/latex] on both sides. Don’t forget to flip the inequality symbol because we divided a number by a negative number.
- First inequality: [latex]2x – 5 > 3x + 2[/latex]
[latex]2x – 5 > 3x + 2[/latex]
[latex]2x – 5 + 5 > 3x + 2 + 5 [/latex]
[latex] 2x > 3x + 7[/latex]
[latex]2x – 3x > 3x – 3x + 7 [/latex]
[latex]-x > 7 [/latex]
[latex]{\Large{{{ – x} \over { – 1}}}} < {\Large{{7 \over { – 1}}}} [/latex]
[latex]\color{red}x < – 7 [/latex]
- Second inequality: [latex]x – 1 < 2x – 5[/latex]
Add both sides by [latex]1[/latex]. Then subtract by [latex]2x[/latex] to both sides. Divide both sides of the inequality by [latex]-1[/latex] thus switching the direction of the inequality symbol.
[latex]x – 1 < 2x – 5[/latex]
[latex]x – 1 + 1 < 2x – 5 + 1[/latex]
[latex]x < 2x – 4 [/latex]
[latex]x – 2x < 2x – 2x – 4[/latex]
[latex] – x < – 4[/latex]
[latex] {\Large{{{ – x} \over { – 1}}}} > {\Large{{4 \over { – 1}}}}[/latex]
[latex]\color{red}x > 4[/latex]
The solutions are given by [latex]\color{red}x < – 7 [/latex] or [latex]\color{red}x > 4[/latex].
STEP 2. Graph the solution set on the number line.
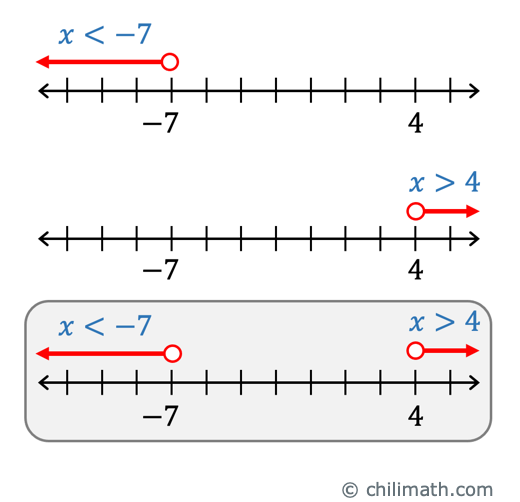
STEP 3. Write the solutions in interval notation.
[latex]\left( { – \infty ,7} \right) \cup \left( {4,\infty } \right)[/latex]
It is as read as “all numbers less than negative [latex]7[/latex] or all numbers greater than [latex]4[/latex]”.
Example 7: Solve the compound inequality [latex]2\left( {x + 1} \right) \le x – 2[/latex] or [latex]3\left( {x – 1} \right) \le 4x – 3[/latex]. Graph the solutions on the number line. Then, write your solutions in interval notation.
STEP 1. Solve each inequality.
- First inequality: [latex]2\left( {x + 1} \right) \le x – 2[/latex]
Distribute 2 into the quantity (x+1). Subtract 2 on both sides of the inequality. Finally, subtract [latex]x[/latex] on both sides to get to the final solution.
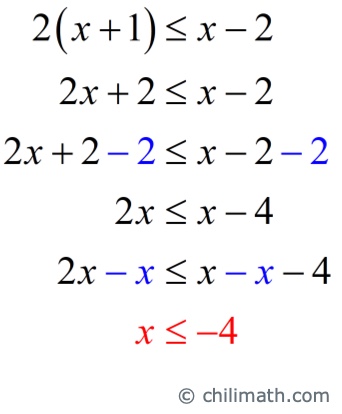
- Second inequality: [latex]3\left( {x – 1} \right) \le 4x – 3[/latex]
Distribute 3 into the quantity (x-1). Next, add 3 to both sides of the inequality. Then, subtract sides by [latex]4x[/latex]. Finally divide both sides by [latex]-1[/latex]. Please don’t forget to switch the direction of the inequality from “less than or equal to” to “greater or equal to”.
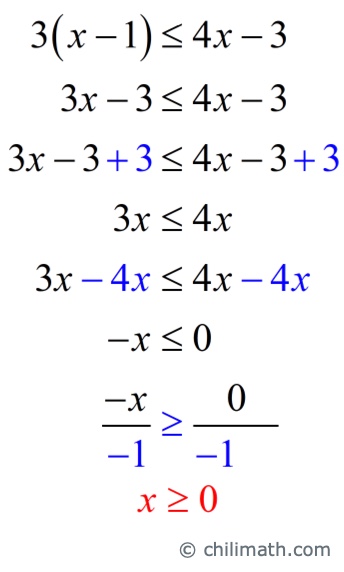
The solutions are given by [latex]\color{red}x \le – 4 [/latex] or [latex]\color{red}x \ge 0[/latex].
STEP 2. Graph the solution set on the number line.
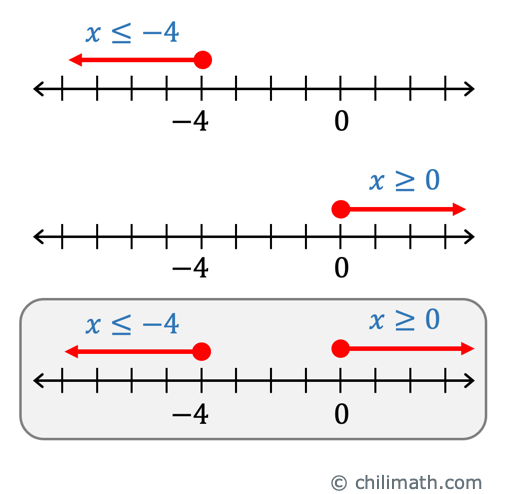
STEP 3. Write the solutions in interval notation.
[latex]\left( { – \infty , – 4} \right) \cup \left( {0,\infty } \right)[/latex]
It is read as “all numbers less than or equal to [latex]-4[/latex] or all numbers greater than or equal to [latex]0[/latex]”.
Example 8: Solve the compound inequality [latex]2\left( {x + 1} \right) – 3\left( {x + 1} \right) < 0[/latex] or [latex]4x + 3 \ge 15 + 6x[/latex]. Graph the solution set on the number line. Then, write the solution set in the interval notation.
STEP 1. Solve each inequality.
- First inequality: [latex]2\left( {x + 1} \right) – 3\left( {x + 1} \right) < 0[/latex]
Apply the Distributive Property of Multiplication over Addition twice on the left of the inequality. Combine similar terms. Add [latex]1[/latex] on both sides. Finally divide both sides of the inequality by [latex]-1[/latex]. Don’t forget to switch the direction of the opening of the inequality symbol since we have divided by a negative number.
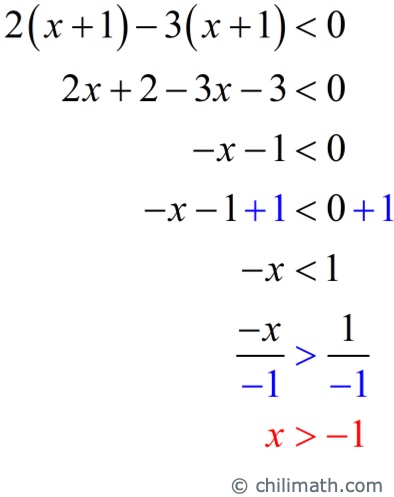
- Second inequality: [latex]4x + 3 \ge 15 + 6x[/latex]
Subtract 3 on both sides, followed by subtracting [latex]6x[/latex]. Divide each side by [latex]-2[/latex] then flip the direction of the inequality.
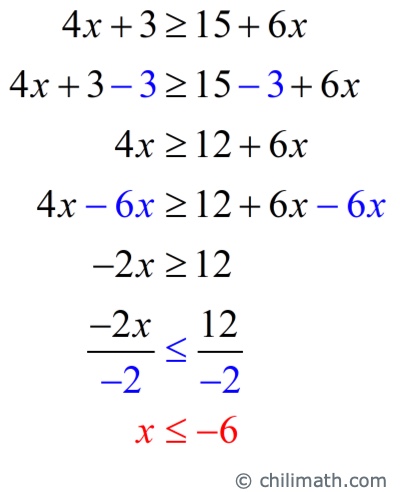
The solutions are given by [latex]\color{red}x > – 1[/latex] or [latex]\color{red}x \le – 6[/latex].
STEP 2. Graph the solution set on the number line.
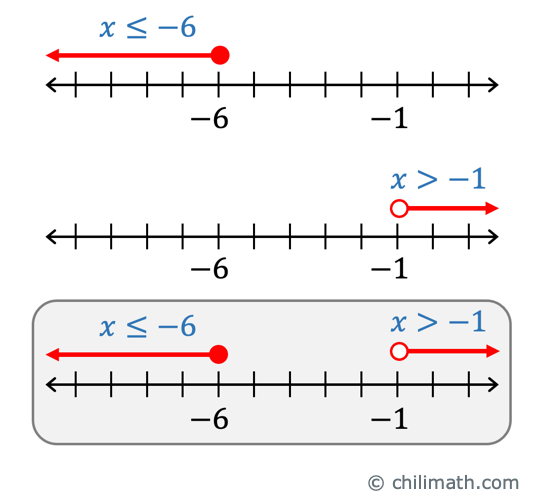
STEP 3. Write the solutions in interval notation.
[latex]\left( { – \infty , – 6} \right] \cup \left( { – 1,\infty } \right)[/latex]
It is read as “all numbers less than or equal to [latex]-6[/latex] or all numbers greater than or equal to [latex]-1[/latex]”.
Example 9: Solve the compound inequality [latex]0 < 3 – \left( {x + 4} \right)[/latex] or [latex]2 < 1 – \left( {x – 2} \right)[/latex]. Graph the solution set on the number line. Then, write the solution set in the interval notation.
STEP 1. Solve each inequality.
- First inequality: [latex]0 < 3 – \left( {x + 4} \right)[/latex]
Apply the Distributive Property on the right side of the inequality then add [latex]x[/latex] to both sides of the inequality.
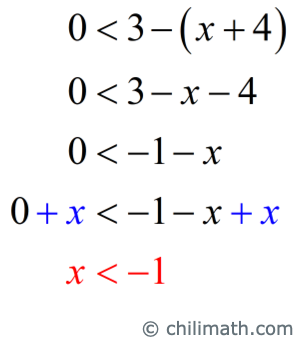
- Second inequality: [latex]2 < 1 – \left( {x – 2} \right)[/latex]
Apply the Distributive Property on the right side then add [latex]x[/latex] to both sides of the inequality. Finally, subtract [latex]2[/latex] on both sides to get to the final answer.
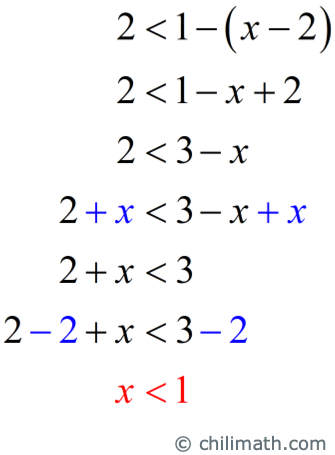
The solutions are given by [latex]\color{red}x < – 1[/latex] or [latex]\color{red}x < 1[/latex].
STEP 2. Graph the solution set on the number line.
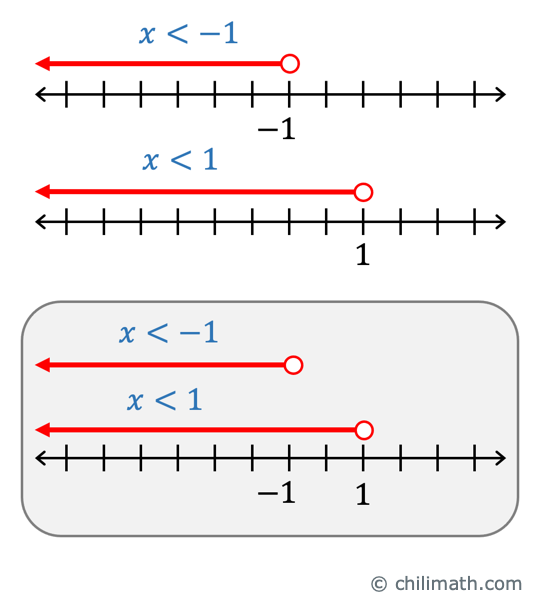
STEP 3. Write the solutions in interval notation.
[latex]\left( { – \infty ,1} \right)[/latex]
It is read as “all numbers less than [latex]1[/latex]”.
Example 10: Solve the compound inequality [latex]10x – 8 < 7x + 7[/latex] or [latex]3x – 2\left( {2 – x} \right) \ge 1[/latex]. Graph the solution set on the number line. Then, write the solution set in the interval notation.
STEP 1. Solve each inequality.
- First inequality: [latex]10x – 8 < 7x + 7[/latex]
Add 8 to both sides. Next, subtract [latex]7x[/latex] on both sides. Finally, divide both sides by positive [latex]3[/latex].
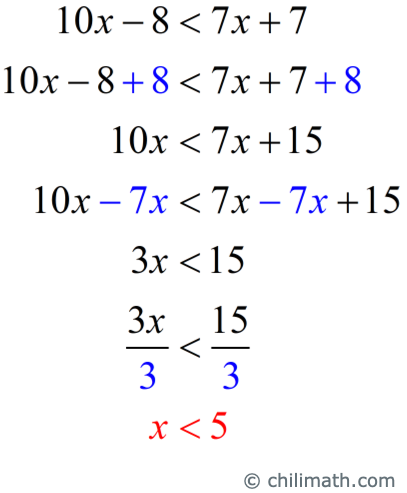
- Second inequality: [latex]3x – 2\left( {2 – x} \right) \ge 1[/latex]
Apply the distributive property on the left side. Combine similar terms. Add [latex]4[/latex] on both sides. Finally, divide [latex]5[/latex] on both sides.
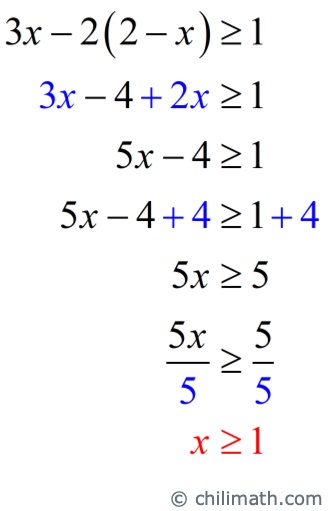
The solutions are given by [latex]\color{red}x < 5[/latex] or [latex]\color{red}x \ge 1[/latex].
STEP 2. Graph the solution set on the number line.
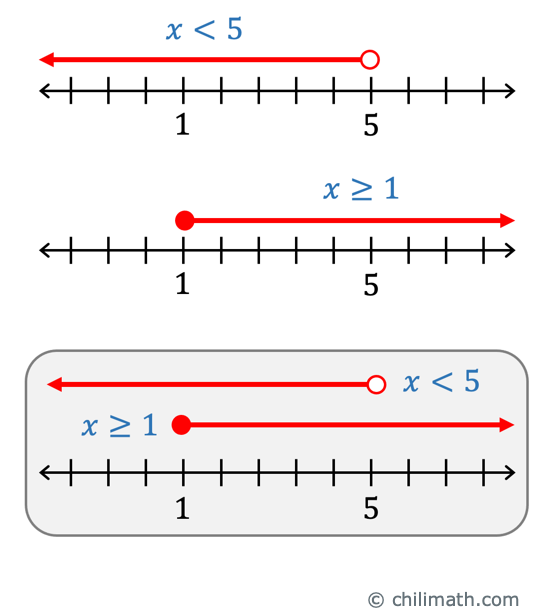
STEP 3. Write the solutions in interval notation.
[latex]\left( { – \infty ,\infty } \right)[/latex]
It is read as ” all real numbers”.
You may also be interested in these related math lessons or tutorials:
