Solving Linear Inequalities
Most of the rules or techniques involved in solving multi-step equations should easily translate to solving inequalities.
The only big difference is how the inequality symbol switches direction when a negative number is multiplied or divided to both sides of an equation.
In this lesson, I will go over seven (7) worked examples with different levels of difficulty to provide enough practice.
Inequality Symbols with Examples and Illustrations on Number Lines
GREATER THAN
- Symbol:

- Example:
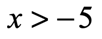
- Graph:

GREATER THAN OR EQUAL TO
- Symbol:

- Example:
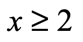
- Graph:
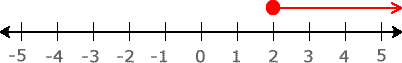
LESS THAN
- Symbol:

- Example:
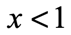
- Graph:

LESS THAN OR EQUAL TO
- Symbol:

- Example:
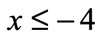
- Graph:
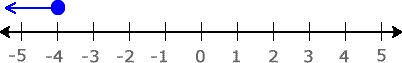
Examples of How to Solve and Graph Linear Inequalities
Example 1: Solve and graph the solution of the inequality
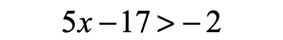
To solve this inequality, we want to find all values of [latex]x[/latex] that can satisfy it. This means there are almost infinite values of [latex]x[/latex] which when substituted, would yield true statements.
Check the values [latex]x = 0[/latex], [latex]x = 1[/latex], [latex]x = 2[/latex], [latex]x = 3[/latex], [latex]x = 5[/latex], [latex]x = 6[/latex] and [latex]x = 7[/latex].
Which of these [latex]x[/latex]-values give back a true statement?
You should agree after performing some back substitutions that only [latex]5[/latex], [latex]6[/latex], and [latex]7[/latex] work; and the rest fail. But the question is, are there more values of [latex]x[/latex] other than the ones mentioned? The answer is yes! Now, let us solve the inequality to figure out the entire set of values that can make it true.
- Write the original problem.
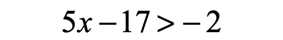
- Add [latex]17[/latex] on both sides to keep the variables on the left side and the constant on the right.
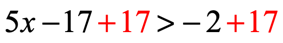
- The inequality is reduced to this after simplifying.
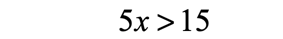
- Divide both sides of the inequality by the coefficient of [latex]x[/latex].
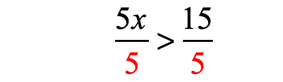
- Final answer:
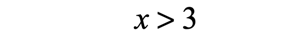
- Use an open hole to indicate that [latex]3[/latex] is not part of the solution. The solution to the inequality [latex]x > 3[/latex] includes all values to the right of [latex]3[/latex] but excluding [latex]3[/latex] itself. Do you see now why all numbers greater than [latex]3[/latex] are solutions?
Example 2: Solve and graph the solution of the inequality
This example illustrates what happens to the inequality symbol when divided by a negative number.
- Write the original problem.
- To isolate variable [latex]x[/latex] to the left of the inequality, I will add both sides by [latex]2[/latex].
- This is how it looks after I simplify using the above step.
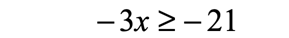
- Now, to solve for [latex]x[/latex], I will divide both sides by [latex] – \,3[/latex].
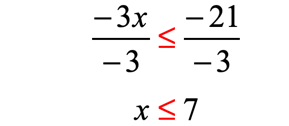
ALWAYS switch the direction of the inequality whenever you divide or multiply a negative number to both sides of the inequality.
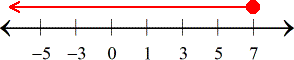
Use a close or shaded hole to indicate that [latex]7[/latex] is part of the solution. The solution of the inequality [latex]x \le 7[/latex] includes [latex]7[/latex] and everything to its left.
Example 3: Solve and graph the solution of the inequality
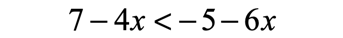
In this problem, I have variables on both sides of the inequality. Although it doesn’t matter where we keep the variable, left or right, it makes sense to be consistent all the time by isolating it on the left side. It’s just a “standard” way, I think.
However, if you try to keep the variable on the right, make sure that you’re aware of their subtleties. For instance, the answer to this problem is [latex]x < – \,6[/latex], which is the same as [latex] – \,6 > x[/latex]. They are equivalent because the opening of the inequality is also pointing towards [latex] – \,6[/latex]. Therefore, this means that if I switch the variable and the constant in my final answer, I must also change the direction of the symbol to keep the meaning the same.
- Write the original problem.
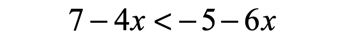
- I want to keep [latex]x[/latex] on the left. I will do that by adding [latex]6x[/latex] to both sides by
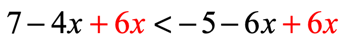
- After the step above, I need to move the constant to the right side.
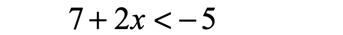
- Subtract both sides by [latex]7[/latex].
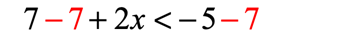
- Simplify
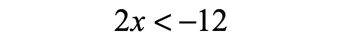
- To finally isolate [latex]x[/latex] on the left, divide both sides by the coefficient of [latex]x[/latex] which is [latex]2[/latex].
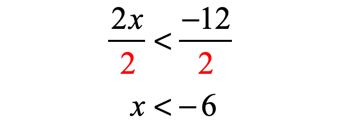
Notice that I did not switch the direction of the inequality because I divided both sides by a positive number.
- Use an open hole to indicate that [latex] – \,6[/latex] is not part of the solution. The solution to the inequality [latex]x < – \,6[/latex] includes all values to the left of [latex] – \,6[/latex] but excluding [latex] – \,6[/latex] itself.
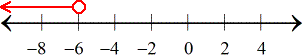
Example 4: Solve and graph the solution of the inequality
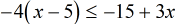
I constructed this problem to emphasize the step required in dealing with the parenthesis symbol. I know that this won’t throw you off because you’ve seen it before when solving linear equations, right? The step required to get rid of the parenthesis is to apply the distributive property of multiplication over addition. However, I must caution you to be careful in dealing with the signs during the multiplication process. Remember, the product of two terms with the same signs is positive and when signs are unlike, the product is negative.
- Write the original problem. I will remove the parenthesis first by distributing that [latex] – \,4[/latex] into the binomial [latex]\left( {x – 5} \right)[/latex].
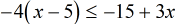
- Simplify and be careful when you distribute. Remember, you get a positive product if the signs are the same and negative if the signs are different.
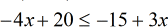
- In solving inequalities, I make it a habit to “always” keep the variable to the left side. Although, keeping it on the right is also correct. This is just a matter of preference. To keep [latex]x[/latex] to the left, subtract both sides by [latex]3x[/latex].
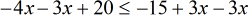
- Since I want the constant to stay on the right, it becomes clear that my next step is to eliminate the [latex]20[/latex] on the left.
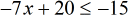
- Subtract both sides by [latex]20[/latex].
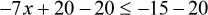
- Obviously, I will divide both sides by the negative coefficient and switch the inequality.
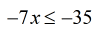
- To solve for [latex]x[/latex], divide both sides by [latex] – \,7[/latex] which leaves us the final answer.
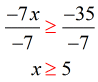
- Use a close or shaded hole to indicate that [latex]5[/latex] is part of the solution. The solution of the inequality [latex]x \ge 5[/latex] includes [latex]5[/latex] and everything to its right.

Example 5: Solve and graph the solution of the inequality
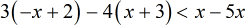
My general approach here is to immediately eliminate the parentheses using the distributive property, combine similar terms on both sides, and finally keep [latex]x[/latex] on the left and the constant to the opposite side.
- Write the original problem. I will apply the distributive property twice on the left side for the two parentheses.
For the right side, they are similar terms so I will simply combine them.
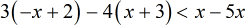
- Simplify. At this point, I will further combine like terms on the left. Combine the [latex]x[/latex]’s and the constants together.
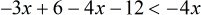
- This is what I got after doing the above step.
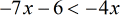
- Move the constants to the right by adding both sides by [latex]6[/latex].
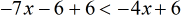
- Simplify.
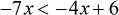
- Now, move all variables to the left by adding both sides by [latex]4x[/latex].
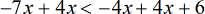
- Divide both sides by [latex] – \,3[/latex] to isolate [latex]x[/latex]. However, I must change the orientation of the inequality symbol since I divided both sides by a negative number.
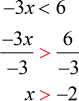
- Use an open hole to indicate that [latex] – \,2[/latex] is not part of the solution. The solution of the inequality [latex]x > – 2[/latex] implies all the values to the right of [latex] – \,2[/latex] but excluding [latex] – \,2[/latex].

Example 6: Solve and graph the solution of the inequality

The “complexity” of this problem should not bother you. The key to successfully solving this is to apply all the techniques you have learned so far from our previous examples. If you need a review, please feel free to take a look back.
Try to solve this problem without looking at the detailed solution. Whenever you think you’re done, compare what you have on paper with the answer below.
- Write the original problem. Get rid of the parentheses on both sides of the inequality by applying the distributive property.

- Simplify. Combine similar terms on both sides.
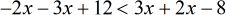
- This is how it looks after combining like terms.
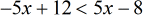
- Subtract both sides by [latex]12[/latex] to keep [latex]x[/latex] on the left.
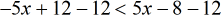
- Simplify.
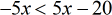
- Subtract both sides by [latex]5x[/latex] to keep the constant on the right.
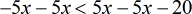
- Solve [latex]x[/latex] by dividing both sides by [latex] – 10[/latex], however, don’t forget to switch the direction of the inequality as well.
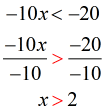
- Use an open hole to indicate that [latex]2[/latex] is not part of the solution. The solution of the inequality includes all values above [latex]2[/latex] but excluding [latex]2[/latex].
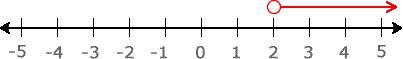
Example 7: Solve and graph the solution of the inequality
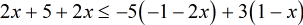
Let’s finish strong by doing one final example for mastery! Again, do this yourself first on paper and then compare your solution with the answer below.
- Write the original problem. Combine the [latex]x[/latex] terms on the left side and then apply the distributive property twice on the right side of the inequality.
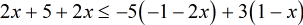
- This is what we got after doing the step above.
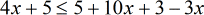
Next, simplify the right side by combing like terms that came out after distribution.
- Simplify.

- To isolate [latex]x[/latex] on the left, subtract both sides by [latex]5[/latex].
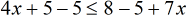
- Simplify.
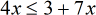
- Get rid of any variables on the right by subtracting [latex]7x[/latex].
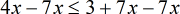
- Finally, divide both sides by [latex] – \,3[/latex] to isolate [latex]x[/latex]. Make sure that we change the direction of the inequality symbol to compensate for the division of a negative number.
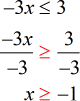
- Use a close or shaded hole to indicate that [latex] – \,1[/latex] is part of the solution. The solution to the inequality [latex]x \ge – 1[/latex] includes [latex] – \,1[/latex] and all values to its right as shown by the direction of the arrow.

You may also be interested in these related math lessons or tutorials:
Steps on How to Graph Linear Inequalities
Graphing Linear Inequalities Examples
Graphing Systems of Linear Inequalities
