Simplifying Expressions Involving Factorials

In this lesson, we will learn how to simplify factorial expressions with variables found in the numerator and denominator. We want to generate common factors in both locations so that they can be canceled. That’s ultimately our goal.

The key is to compare the factorials and determine which one is larger in value. Suppose we want to compare the factorials [latex]\left( {n + 3} \right)![/latex] and [latex]\left( {n + 1} \right)![/latex] .

It is easy to see that [latex]\left( {n + 3} \right)! > \left( {n + 1} \right)![/latex] is true for all values of [latex]n[/latex] as long as the factorial is defined, that is, the stuff inside the parenthesis is a whole number greater than or equal to zero.

  • That means we can expand [latex]\left( {n + 3} \right)![/latex] until such time the expression [latex]\left( {n + 1} \right)![/latex] appears in the sequence.
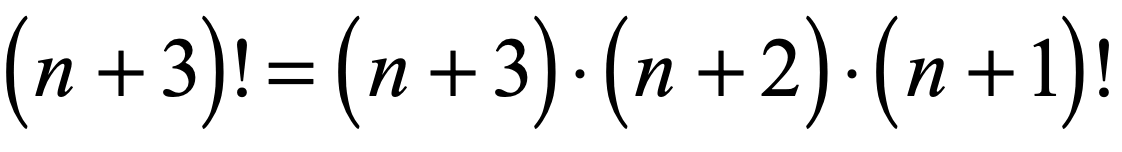
(n+3)!=(n+3)(n+2)(n+1)!

How about for [latex]\left( {n – 5} \right)![/latex] and [latex]\left( {n – 2} \right)![/latex] ? This time we are subtracting the variable by some number. The larger expression is the one with smaller subtrahend, or the value being subtracted from the minuend. Therefore, [latex]\left( {n – 2} \right)! > \left( {n – 5} \right)![/latex] .

  • That implies the expression [latex]\left( {n – 2} \right)![/latex] will have [latex]\left( {n – 5} \right)![/latex] in its expanded form.
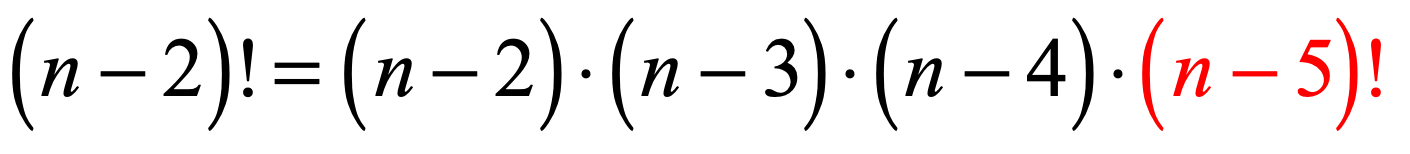
(n-2)!=(n-2)(n-3)(n-4)(n-5)!

What if they have different signs?

Obviously, the larger factorial expression is the one with the addition operation.

For example, [latex]\left( {n + 1} \right)! > \left( {n – 4} \right)![/latex] .

  • Observe, we can expand [latex]\left( {n + 1} \right)![/latex] to include [latex]\left( {n – 4} \right)![/latex] in the sequence.
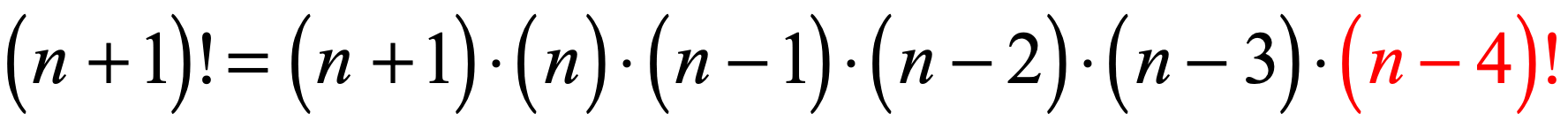
(n+1)!=(n+1)(n)(n-1)(n-2)(n-3)(n-4)!

Key Steps on How to Simplify Factorials involving Variables

  1. Compare the factorials in the numerator and denominator.
  2. Expand the larger factorial such that it includes the smaller ones in the sequence.
  3. Cancel out the common factors between the numerator and denominator.
  4. Simplify further by multiplying or dividing the leftover expressions.

Let’s go over six (6) examples with varying levels of difficulty.

Examples of Simplifying Factorials with Variables

Example 1: Simplify

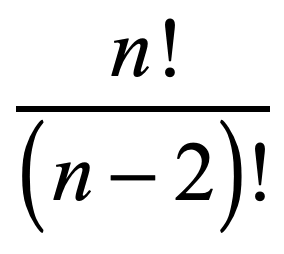
n! divided by (n-2)!

Since the factorial expression in the numerator is larger than the denominator, I can partially expand [latex]n![/latex] until the expression [latex]\left( {n – 2} \right)![/latex] shows up which is the value in the denominator. Then I will cancel the common factors. Apply the distributive property to get to the final answer.

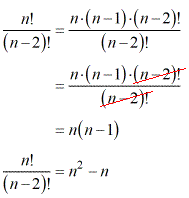
n! divided by (n-2)! = n^2-n

Example 2: Simplify

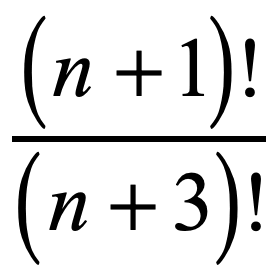
(n+1)1 divided by (n+3)!

Obviously, the denominator is larger than the numerator because [latex]3[/latex] is being added to “[latex]n[/latex]” as compared to being added by [latex]1[/latex]. I will keep the numerator unchanged while expanding the denominator [latex]\left( {n + 3} \right)![/latex] until the expression [latex]\left( {n + 1} \right)![/latex] appears in the denominator. What we are doing is matching common factors so we can cancel them out. Multiply the two binomials in the denominator to finish it off.

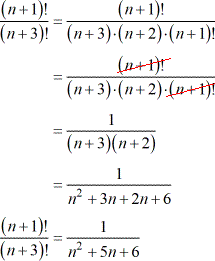
(n+1)1 divided by (n+3)! = 1/(n^2+5n+6)

Example 3: Simplify

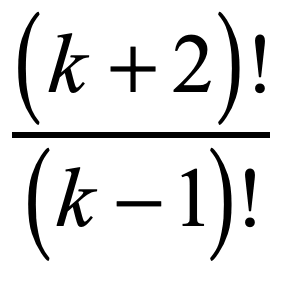
(k+2)! divided by (k-1)!

The numerator [latex]\left( {k + 2} \right)![/latex] can be expanded into factors that would include the denominator [latex]\left( {k – 1} \right)![/latex] . By doing so, we can cancel out duplicate factors between the numerator and denominator. Multiply together the leftover factors: two binomials and a monomial.

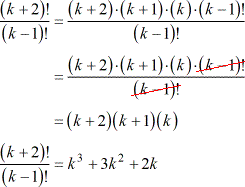
(k+2)! divided by (k-1)! = k^3+3k^2+2k

Example 4: Simplify

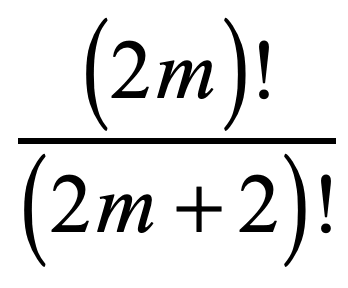
(2m)! divided by (2m+2)!

The denominator is the bigger factorial expression, so I will expand it such that I get the numerator. Cancel out the common factors and multiply the binomials to arrive at the final answer.

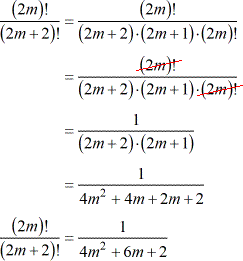
(2m)! divided by (2m+2)! = 1/(4m^2+6m+2)

Example 5: Simplify

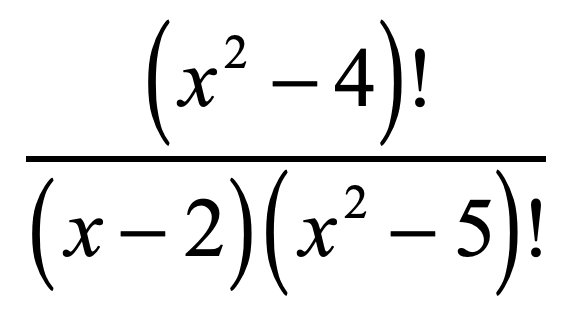
(x^2-4)! divided by (x-2)(x^2-5)!

I will expand the factorial in the numerator which is [latex]\left( {{x^2} – 4} \right)![/latex] to get the factorial in the denominator which is [latex]\left( {{x^2} – 5} \right)![/latex] so we can cancel them out. In addition, I will leave alone the binomial [latex]\left( {x – 2} \right)[/latex] found in the denominator. Don’t expand it because it doesn’t have the factorial symbol.

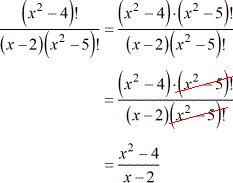
(x^2-4)! divided by (x-2)(x^2-5)! = (x^2-4)/(x-2)

After cancellations, observe that the numerator is a quadratic term that can be factored out into two binomials.

That is, [latex]\left( {{x^2} – 4} \right) = \left( {x + 2} \right)\left( {x – 2} \right)[/latex].

I hope you can see that we generated common factors that can be canceled out one more time. This greatly simplifies our final answer.

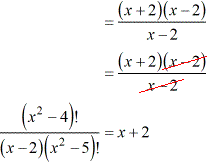
(x^2-4)! divided by (x-2)(x^2-5)! = x+2

Example 6: Simplify

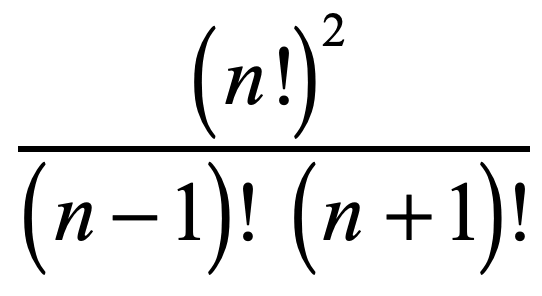
(n!)^2 divided by (n-1)! (n+1)!

Notice that [latex]n![/latex] is being squared in the numerator. That means [latex]{\left( {n!} \right)^2} = \left( {n!} \right)\left( {n!} \right)[/latex] . As part of our strategy, we can also separate the original problem into two separate fractions. This allows us to see much better what’s going on. Perform the necessary expansions and cancel out common factors. Simplify by writing back the final answer as one fraction.

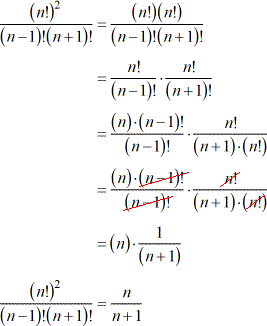
(n!)^2 divided by (n-1)! (n+1)!=n/(n+1)

You may also be interested in these related math lessons or tutorials:

Factorial Notation, Formula, and Basic Examples
Dividing Factorials
Zero Factorial