Dividing Factorials

After learning how to evaluate an individual factorial expression, we are now ready to divide factorials. They come in the form of fractions because the numerator and denominator contain factorials. To simplify such type of problem, expand the factorials on top and at the bottom, cancel out common factors, and finish off by simplifying the leftover numbers.

Here are some examples.

Examples of How to Divide Factorials involving Whole Numbers

Example 1: Simplify by dividing the factorial below.

9!/7!

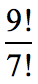
We expand the numerator and denominator using the definition of factorial. That means, count down from 9 to 1 for the numerator, and 7 to 1 for the denominator. Cancel out common factors in the numerator and denominator to simplify.

9 factorial divided by 7 factorial equals 9 times 8 equals 72

Alternative solution:

Do we really need to fully expand the factorial? The answer is no. The better approach is to expand 9! until it reaches 7! because that is the factorial value in the denominator. This would allow us to cancel them out easily leaving us with less clutter in the calculation.

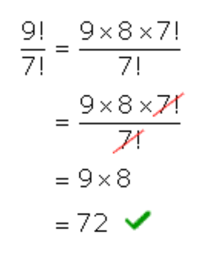
9!/7!=9x8=72

Just to check our answer with a calculator,

calculator check 9!/7!=72

Example 2: Simplify by dividing the factorial below.

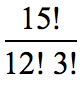
15!/(12! * 3!)

I would expand 15! until I get 12! because that is the factorial in the denominator. They should cancel out nicely. Then I will simplify what is left. I am not so worried of 3! in the denominator because it is rather a small number.

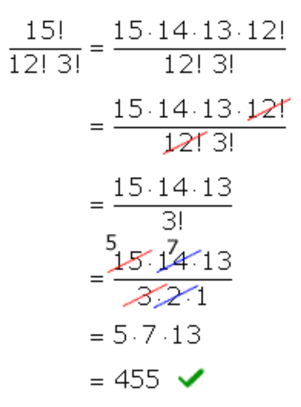
(15!)/(12!*3!)=5*7*13=455

Calculator check,

calculator check (15!)/(12!*3!)=455

Example 3: Simplify the factorial expression below by division .

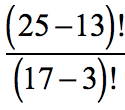
(25-13)!/(17-3)!

CAUTION: Don’t interpret the problem as distributing the “factorial operation” by multiplying it into the numbers inside the parenthesis.

The following is an example of what NOT to do. This is a common mistake that I’ve seen with my students.

(3 – 1)! = 3! – 1! = (3) (2) (1) â€“ 1 = 6 âˆ’ 1 = 5  <–Wrong Answer!

The correct approach is to combine the stuff inside the parenthesis first, then apply the factorial operation.

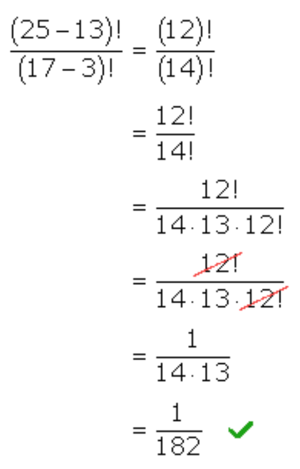
(25-13)!/(17-3)!=12!/14!=1/(14*13)=1/182

The calculator agrees with our answer.

calculator check (25-13)!/(17-3)!=1/182

You may also be interested in these related math lessons or tutorials:

Factorial Notation, Formula, and Basic Examples
Simplifying Factorials with Variables
Zero Factorial