Factoring Perfect Square Trinomial
A perfect square trinomial can be factored out as binomial multiplied to itself. That means we can write a perfect square trinomial as a square of a binomial.
First, let’s expand a binomial to see if we can observe a pattern.
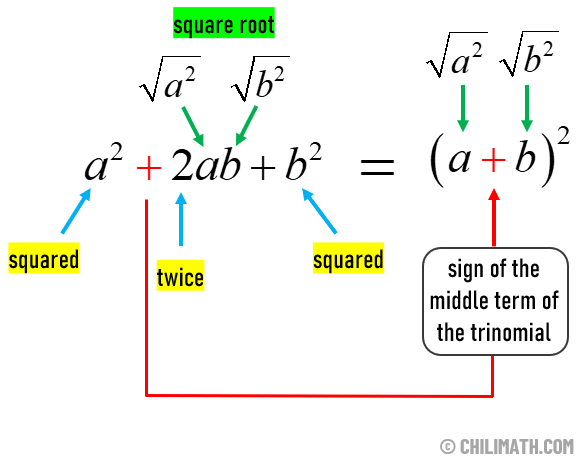
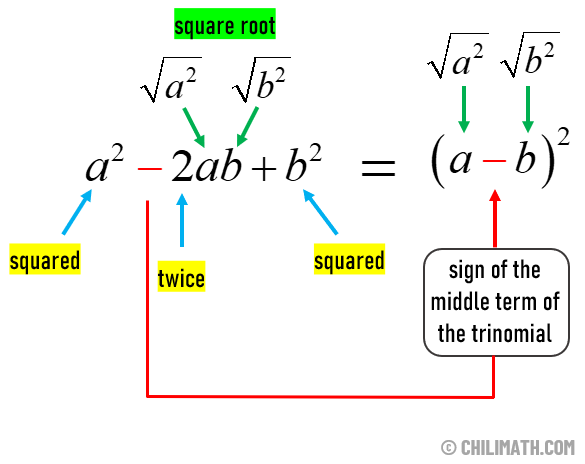
Notice that the first and the last terms are perfect squares. The middle term is twice the product of the terms that are being squared. If the binomial is positive, the middle term of the trinomial is positive. Similarly, if the binomial is negative, the middle term of the trinomial is negative.

To factor a perfect square trinomial into a square of binomial, we need to be able to recognize the pattern then simply reverse the process.
In summary, we need to verify that:
- The first term is a square term, that is, [latex]a^2[/latex]
- The last term is a square term, that is, [latex]b^2[/latex]
- The middle term is twice the product of the square roots of the first and last terms, that is, [latex]2ab[/latex]
- If conditions #1, #2, and #3 are met, then we can rewrite the trinomial as a square of a binomial.
- Just note that the sign of the middle term of the trinomial determines the sign of the binomial.
CASE 1: If the middle sign of the trinomial is positive, then the middle sign of binomial is also positive.
CASE 2: If the middle sign of the trinomial is negative, then the middle sign of binomial is also negative.
Examples of Factoring Perfect Square Trinomial
Example 1: Factor [latex]{x^2} + 8x + 16[/latex]
Let’s examine if the given trinomial meets the requirements.
The first term [latex]x^2[/latex] is a perfect square since it can be written as [latex]x^2=(x)^2[/latex].
The last term [latex]16[/latex] is a perfect square since it can be written as [latex]16=(4)^2[/latex].
We will now check if the middle term of the trinomial is twice the product of the square roots of the first and the last terms.
The square root of the first term is [latex]\sqrt {{x^2}} = \sqrt {{{\left( x \right)}^2}} = x[/latex].
The square root of the last term is [latex]\sqrt {16} = \sqrt {{{\left( 4 \right)}^2}} = 4[/latex].
Therefore, [latex]2\left( 4 \right)\left( x \right) = 8x[/latex] which is exactly the middle term of the given trinomial.
It means the trinomial [latex]{x^2} + 8x + 16[/latex] fits the requirements of a perfect square trinomial.
Since the middle term of the trinomial is positive, the middle term of the binomial will also be positive. Thus, we can use the formula below to factor the trinomial.
[latex]{a^2} + 2ab + {b^2} = {\left( {a + b} \right)^2}[/latex]
[latex]{x^2} + 8x + 16 = {\left( x \right)^2} + 2\left( x \right)\left( 4 \right) + {\left( 4 \right)^2} = {\left( {x + 4} \right)^2}[/latex]
Example 2: Factor [latex]9x^2-30x+25[/latex]
Observe that the first and the last terms are perfect squares because
[latex]9x^2=(3x)^2[/latex]
[latex]25=(5)^2[/latex]
Then we will check if the middle term is twice the product of the square roots of the first and last terms.
[latex]2 \cdot \sqrt {{{\left( {3x} \right)}^2}} \cdot \sqrt {{{\left( 5 \right)}^2}} = 2\left( {3x} \right)\left( 5 \right) = 30x[/latex]
Yes, it is! It means the given trinomial [latex]9x^2-30x+25[/latex] is a perfect square trinomial.
Note that the middle term of the given trinomial is negative therefore the middle term of the binomial must be also negative.
[latex]{a^2} – 2ab + {b^2} = {\left( {a – b} \right)^2}[/latex]
[latex]9{x^2} – 30x + 25 = {\left( {3x} \right)^2} – 2\left( {3x} \right)\left( 5 \right) + {\left( 5 \right)^2} = {\left( {3x – 5} \right)^2}[/latex]
Example 3: Factor [latex]49{x^2} – 28xy + 4{y^2}[/latex]
At first look, the problem may look intimidating because this is a bit different than the previous examples. However, if we just apply the things that we already know we should be able to figure out how to factor this out.
Start by asking if the first and last terms are perfect squares. Actually, they are since
[latex]49{x^2} = {\left( {7x} \right)^2}[/latex]
[latex]4{y^2} = {\left( {2y} \right)^2}[/latex]
Now, let’s find out if twice the product of the square roots of the first and last terms is equal to the middle term of the trinomial.
[latex]\sqrt {49{x^2}} = \sqrt {{{\left( {7x} \right)}^2}} = 7x[/latex]
[latex]\sqrt {4{y^2}} = \sqrt {{{\left( {2y} \right)}^2}} = 2y[/latex]
That means,
[latex]2\left( {7x} \right)\left( {2y} \right) = 28xy[/latex]
So it is! Thus, the trinomial [latex]49{x^2} – 28xy + 4{y^2}[/latex] is a perfect square trinomial.
Let’s apply the formula to factor the trinomial. Use the formula where the middle term of the trinomial is negative as shown below.
[latex]{a^2} – 2ab + {b^2} = {\left( {a – b} \right)^2}[/latex]
[latex]49{x^2} – 28xy + 4{y^2} = {\left( {7x} \right)^2} – 2\left( {7x} \right)\left( {2y} \right) + {\left( {2y} \right)^2} = {\left( {7x – 2y} \right)^2}[/latex]
Example 4: Factor [latex]100{x^2} + 20xyz + {y^2}{z^2}[/latex]
Let’s do one last example! This particular trinomial has three variables. Are the first and last terms perfect squares? Checking each term, we have
[latex]100{x^2} = {\left( {10x} \right)^2}[/latex]
[latex]{y^2}{z^2} = {\left( {yz} \right)^2}[/latex]
Absolutely! They are perfect squares. Now, we will check if the middle term if twice the square roots of the first and last terms.
[latex]2 \cdot \sqrt {{{\left( {10x} \right)}^2}} \cdot \sqrt {{{\left( {yz} \right)}^2}} = 2\left( {10x} \right)\left( {yz} \right) = 20xyz[/latex]
It also matches the middle term of the trinomial that means the trinomial in question is a perfect square trinomial. We can proceed with the factorization.
[latex]100{x^2} + 20xyz + {y^2}{z^2} = {\left( {10x} \right)^2} + 2\left( {10x} \right)\left( {yz} \right) + {\left( {yz} \right)^2} = {\left( {10x + yz} \right)^2}[/latex]
You may also be interested in these related math lessons or tutorials:
