Factoring Difference of Two Perfect Squares
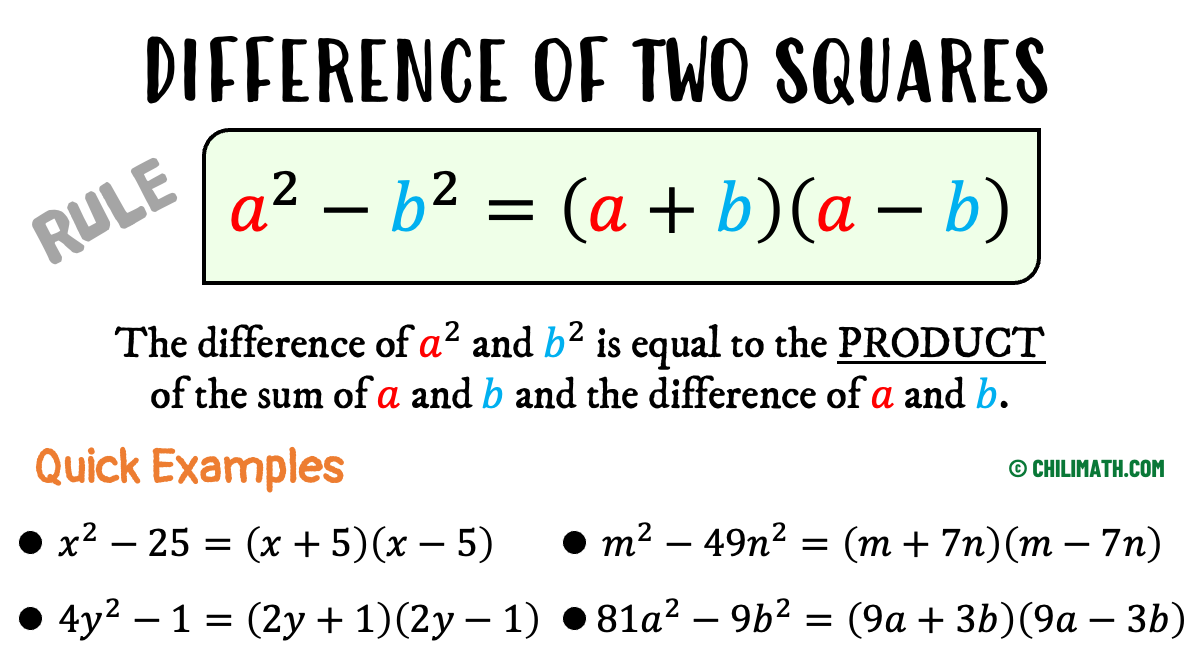
At some point in your study of algebra, you’ll be asked to factor expressions by recognizing some special patterns. The difference of two squares is one of the most common. The good news is, this form is very easy to identify.
Whenever you have a binomial with each term being squared (having an exponent of [latex]2[/latex]), and they have subtraction as the middle sign, you are guaranteed to have the case of difference of two squares.
The diagram below should provide an intuitive understanding of this concept.
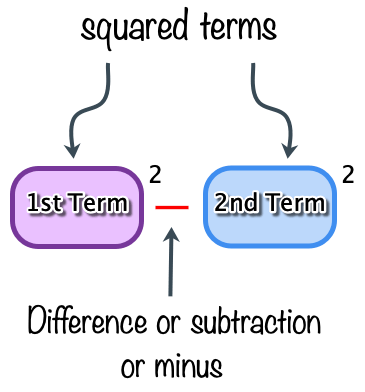
After verifying that you have a difference of two squares, you can now factor it out as a product of two binomials with alternating signs in the middle, positive and negative.
Formula for Difference of Two Squares

These are other ways to write the formula of the difference of two squares using variables. Learn to recognize them in various appearances so that you know exactly how to handle them.
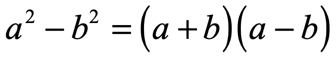
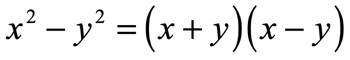
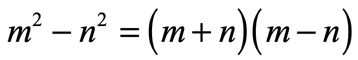
Examples of How to Factor Difference of Two Perfect Squares
Let’s go over some examples!
Example 1: Factor the binomial below using the difference of two squares method.
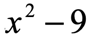
The first term of the binomial is definitely a perfect square because the variable [latex]x[/latex] is being raised to the second power. However, the second term of the binomial is not written as a square. So we need to rewrite it in such a way that [latex]9[/latex] is expressed as some number with a power of [latex]2[/latex]. I hope you can see that [latex]9 = {\left( 3 \right)^2}[/latex]. Clearly, we have a difference of two squares because the sign between the two squared terms is subtraction.
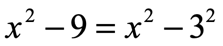
For this example, the solution is broken down in just a few steps to highlight the procedure. Once you get comfortable with the process, you can skip a lot of steps. In fact, you can go straight from the difference of two squares to its factors.
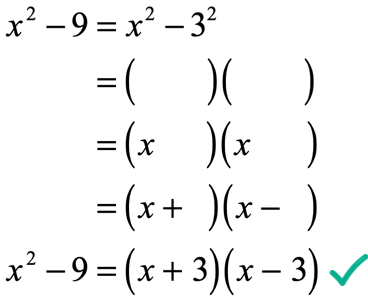
Example 2: Factor the binomial below.
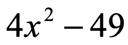
At first, it appears that this is not a difference of two squares. What we need is to try rewriting it in the form that is easily recognizable.
For the first term of the binomial, what term when multiplied by itself gives [latex]4{x^2}[/latex]? That should be [latex]2x[/latex] since
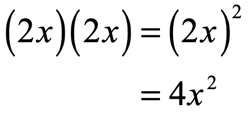
For the second term, the number when multiplied by itself gives [latex]49[/latex] is [latex]7[/latex] because
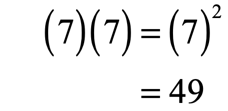
The solution to this problem looks like this,
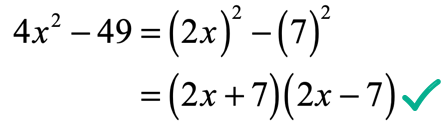
Example 3: Factor the binomial below.
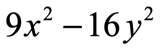
This problem is a little bit different because both terms of the binomial contain variables. If we can show that they are perfect squares then we should be alright!
- The first term is a perfect square since
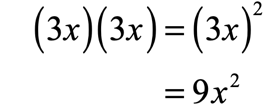
- More so, the second is also a perfect square because
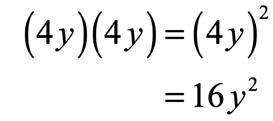
Applying the formula for the difference of two squares we get,
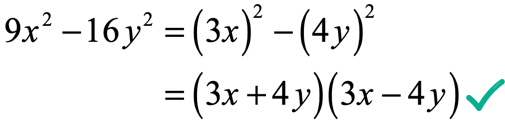
Example 4: Factor the binomial below.
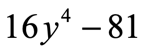
Here’s an interesting problem. Maybe you already recognize that the pure numbers, [latex]16[/latex] and [latex]81[/latex], are perfect squares. That’s good. The variable [latex]y[/latex] though doesn’t have an exponent of [latex]2[/latex], but instead has an exponent of [latex]4[/latex]. Does this qualify to be a square?
Don’t be quick to conclude that it is not. Can you think of a term which when multiplied by itself gives [latex]{y^4}[/latex]? You can do a trial and error on this. But if you apply your previous knowledge of the Product Rule of Exponents, it makes sense that
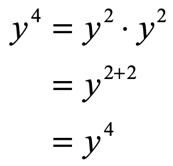
In fact, whenever the exponent of a variable is an even number, that expression can be expressed as a perfect square. Why? Because all even numbers are factorable by the number [latex]2[/latex].
Now, we can truly rewrite this binomial as the difference of two squares with distinct terms that are being raised to the second power; where [latex]16{y^4} = {\left( {4{y^2}} \right)^2}[/latex] and [latex]81 = {\left( 9 \right)^2}[/latex]
Putting this together, we get
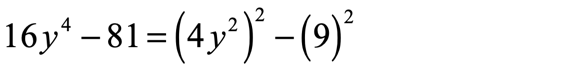
Now you can break this up into two binomial factors with alternating signs,
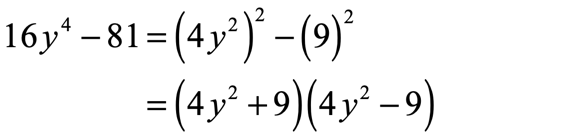
Are we done already? Well, examine carefully the binomials you factored out. The second parenthesis is possibly a case of difference of two squares as well since [latex]4{y^2} = \left( {2y} \right)\left( {2y} \right)[/latex] and clearly, [latex]9 = \left( 3 \right)\left( 3 \right)[/latex].
This means you have to apply the formula for the difference of two squares one more time.
Here’s the complete solution to this problem.

Example 5: Factor the binomial below.

Notice that the binomial has only one kind of variable which is “[latex]x[/latex]”. The basic strategy when you see something similar to this is to factor out the greatest common factor (GCF) among the variables.
Between [latex]{x^4}[/latex] and [latex]{x^{12}}[/latex], the GCF is [latex]{x^4}[/latex]. If you factor this out, you get
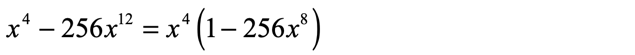
Now we can deal with the binomial inside the parenthesis. It is actually a difference of two squares because we can express each term of the binomial as an expression with a power of [latex]2[/latex].
![x^4-256x^12=x64[(1)^2-(16x^4)^2]](https://www.chilimath.com/wp-content/uploads/2019/01/factdiff-ex5c.png)
Then we apply the formula for the difference of two squares,
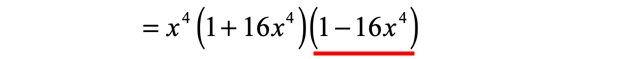
Are we done? Nope! The second parenthesis is still a case of difference of two squares. We have no choice but to factor it out one more time.
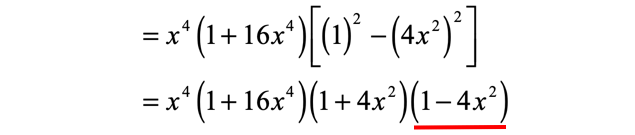
Scan through the binomials again to see if there is still a case of difference of two squares. The last binomial definitely fits the criteria.
Let’s work this out one last time and we’re done!
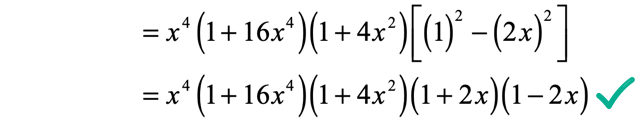
Example 6: Factor the binomial below.
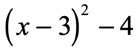
I want to throw in this type of problem because you may encounter something similar to this in your studies. First, recognize that it is a binomial where the first term is [latex]{\left( {x – 3} \right)^2}[/latex] and the second term is [latex]4[/latex]. Since both are squared terms and being separated by subtraction, this is truly a case of difference of two squares.
![(x-3)^2=[(x-3)+2][(x-3)-2]](https://www.chilimath.com/wp-content/uploads/2019/01/factdiff-ex6b.png)
You may keep it in that form as your final answer. But the best answer is to combine like terms by adding or subtracting the constants. This also simplifies the answer by getting rid of the inner parenthesis.
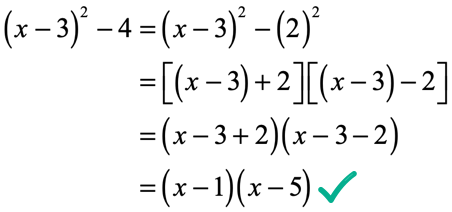
You may also be interested in these related math lessons or tutorials:
Factoring Difference of Two Squares Practice Problems
Factoring Sum and Difference of Two Cubes
Factoring Sum and Difference of Two Cubes Practice Problems
