Inverse Variation (also known as Inverse Proportion)
The concept of inverse variation is summarized by the equation below.
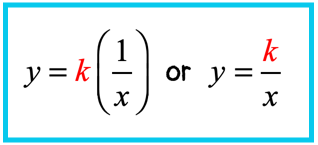
Key Ideas of Inverse Variation
- We say that [latex]y[/latex] varies inversely with [latex]x[/latex] if [latex]y[/latex] is expressed as the product of some constant number [latex]k[/latex] and the reciprocal of [latex]x[/latex].
- However, the value of [latex]k[/latex] can’t equal zero, i.e. [latex]k \ne 0[/latex].
- Isolating [latex]k[/latex] on one side, it becomes clear that [latex]k[/latex] is the fixed product of [latex]x[/latex] and [latex]y[/latex]. That means, multiplying [latex]x[/latex] and [latex]y[/latex] always
yields a constant output of [latex]k[/latex].
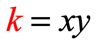
[latex]k[/latex] is also known as the constant of variation, or constant of proportionality.
Examples of Inverse Variation
Example 1: Tell whether [latex]y[/latex] varies inversely with [latex]x[/latex] in the table below. If yes, write an equation to represent for the inverse variation.
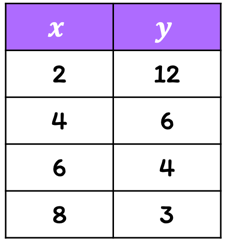
Solution:
In order for the table to have an inverse variation characteristic, the product for all pairs of [latex]x[/latex] and [latex]y[/latex] in the data set must be the same.

The product of variables [latex]x[/latex] and [latex]y[/latex] is constant for all pairs of data. We can claim that [latex]k = 24[/latex] is the constant of variation. Writing the equation of inverse proportionality,
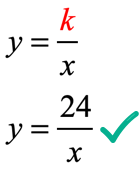
Here is the graph of the equation [latex]y = {{24} \over x}[/latex] with the points from the table.
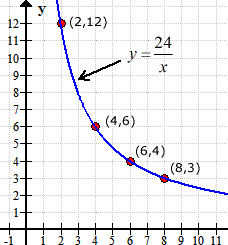
Example 2: Tell whether [latex]y[/latex] varies inversely with [latex]x[/latex] in the table below. If yes, write an equation to represent for the inverse variation.
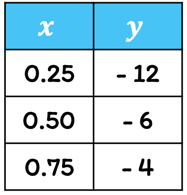
Solution:
If the data in the table represents inverse variation, the product of [latex]x[/latex] and [latex]y[/latex] must be a constant number.

Obviously, multiplying [latex]x[/latex] and [latex]y[/latex] together yields a fixed number. This becomes our constant of variation, thus [latex]k = – \,3[/latex]. The equation of inverse variation is written as,
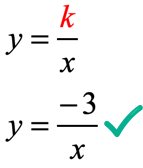
This is the graph of [latex]y = {{ – \,3} \over x}[/latex] with the points from the table.
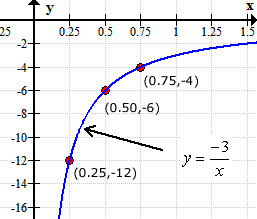
Example 3: Given that [latex]y[/latex] varies inversely with [latex]x[/latex]. If [latex]x = – \,2[/latex] then [latex]y = 14[/latex].
a) Write the equation of inverse variation that relates [latex]x[/latex] and [latex]y[/latex].
b) What is the value of [latex]y[/latex] when [latex]x = 4[/latex]?
Part a) Write the equation of inverse variation that relates [latex]x[/latex] and [latex]y[/latex].
- Begin by writing the general formula of inverse variation which is [latex]y = {k \over x}[/latex]. This gives us the idea that we can solve for [latex]k[/latex] since the values of [latex]x[/latex] and [latex]y[/latex] are given.
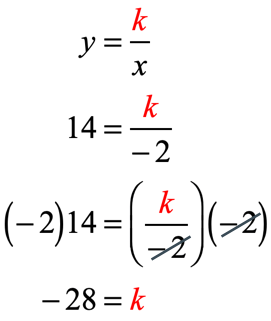
- Now we can write the inverse variation equation that relates [latex]x[/latex] and [latex]y[/latex].
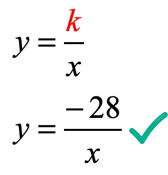
Part b) What is the value of [latex]y[/latex] when [latex]x = 4[/latex]?
- To solve for [latex]y[/latex], substitute [latex]x = 4[/latex] into the equation found in part a).
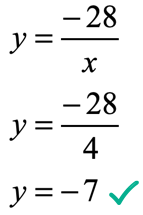
Example 4: If [latex]y[/latex] varies inversely with [latex]x[/latex], find the missing value of [latex]y[/latex] in

Solution:
Use the first point [latex]\left( {4, – \,2} \right)\,[/latex] to determine the value of [latex]k[/latex] using the formula [latex]y = {k \over x}[/latex] .
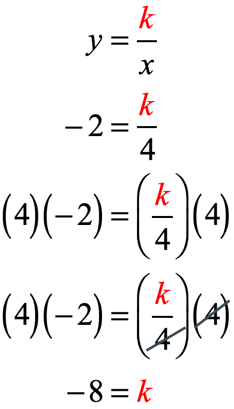
Writing the equation of inverse variation that relates [latex]x[/latex] and [latex]y[/latex],
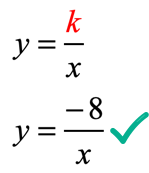
To solve for the missing value of [latex]y[/latex] in the point [latex]\left( { – \,8,y} \right)[/latex], just plug in the value of [latex]x[/latex] in the formula found above then simplify.
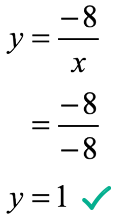
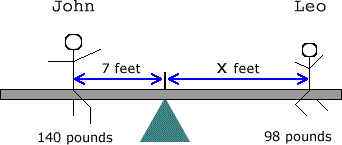
Example 5: To balance a lever (seesaw), the weight varies inversely with the distance of the object from the fulcrum. If John, weighing 140 pounds, is sitting 7 feet from the fulcrum, where should his brother Leo who weighs 98 pounds should sit in order to balance the seesaw?
Solution:
It is important to draw a sketch of the scenario so that we have an idea what’s going on.
We are told that weight varies inversely with distance. That means, our formula for inverse variation relating the weight and distance is:
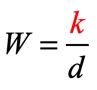
We can find the value of [latex]k[/latex] using the information of John because both his weight and distance from the fulcrum are clearly given in the problem.
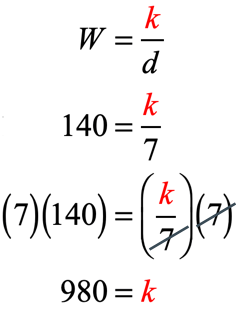
Below is the equation of inverse variation relating weight and distance.
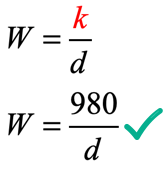
Remember that we are trying to find how far Leo, weighing 98 pounds, should sit from the fulcrum to balance the seesaw. To do that, substitute the weight of Leo in the formula found above and solve for “[latex]d[/latex]”.
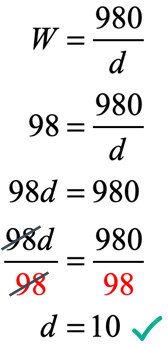
Therefore, Leo needs to sit 10 feet away from the fulcrum to balance the seesaw!
You may also be interested in these related math lessons or tutorials:
