Finding the Domain and Range of Radical and Rational Functions

This time we will tackle how to find the domain and range of more interesting functions, namely, radical functions and rational functions. We will take a look at two (2) examples on how to find the domain and range of radical functions, and also two (2) examples of rational functions.

If you would like to review, I also have a separate lesson on how to find the domain and range of linear and quadratic functions.

---

Examples of How to Find the Domain and Range of Radical and Rational Functions

Example 1: Find the domain and range of the radical function

[latex]y = \sqrt {x – 2}[/latex]

Remember that I can’t have [latex]x[/latex]-values which can result in having a negative number under the square root symbol. To find the domain (“good values of [latex]x[/latex]”), I know that it is allowable to take the square root of either zero or any positive number. My plan is to find all the values of [latex]x[/latex] satisfying that condition. It will become the domain itself.

I would let the expression under the radical, [latex]x-2[/latex], greater than or equal to zero; and then solve the inequality. Check out my other lesson on how to solve inequalities.

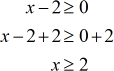
This radical function has a domain of x ≥ 2. I need to be careful in finding the range of this function. The graph of the function looks like this.

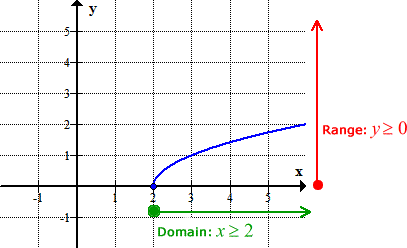
The radical function starts at [latex]y = 0[/latex] and can go as high as it wants (positive infinity). You may think that this function grows slowly (slow increase in [latex]y[/latex] values) and thus can’t reach extremely large values. However, you must consider that plugging in a sufficiently large value of [latex]x[/latex] ( i.e. in billions of trillions) can result in a very large output value of [latex]y[/latex].

Therefore, I will claim that the range of this function is y ≥ 0.

This is the summary of the domain and range written both in set and interval notations.

---

Example 2: Find the domain and range of the radical function

[latex]y = – \sqrt {10 – 2x} [/latex]

The acceptable values under the square root are zero and positive numbers. So I will let the “stuff” inside the radical equal to or greater than zero, and then solve for the required inequality.

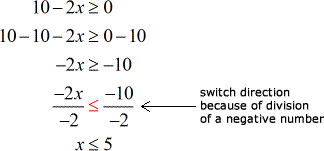
Now, the domain of the function is x ≤ 5. Just like in our previous examples, I will graph the function to determine the range.

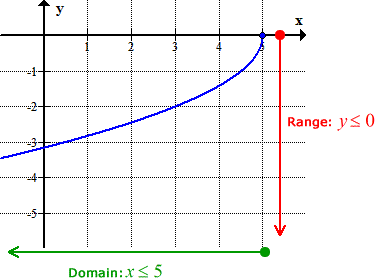
The radical function starts at [latex]y = 0[/latex], and then slowly but steadily decreases in values all the way down to negative infinity. This makes the range y ≤ 0. Below is the summary of both domain and range.

---

Example 3: Find the domain and range of the rational function

[latex]\Large{y = {5 \over {x – 2}}}[/latex]

This function contains a denominator. This tells me that I must find the [latex]x[/latex]-values that can make the denominator zero to prevent the undefined case from happening.

Here, our domain is all x-values but does not include x = 2. It makes a lot of sense because I can plug any values of [latex]x[/latex] into the function with the exception of [latex]x = 2[/latex], and the function will have valid outputs. The graph below shows that [latex]x = 2[/latex] is actually a vertical asymptote (see the dashed orange line).

To find the range is a bit tricky. Looking at the graph carefully, I see that it goes up without any limit and goes down without any limit as well. However, I won’t rush to claim that the range is all [latex]y[/latex] values. There is something going on as the graph moves to the right without bound. Do you see that it gets closer and closer to zero? Similarly, this characteristic is also happening as the graph moves to the left without bound. It also gets very close to zero but not quite. This quick analysis gives me the intuition that maybe y cannot equal zero.

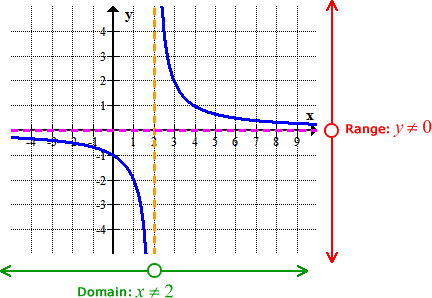
Doing some “common sense” analysis to show that y cannot equal zero [latex](y ≠ 0)[/latex].

Going back to the original function

[latex]\Large{y = {5 \over {x – 2}}}[/latex]

If I want [latex]y[/latex] to equal zero, I need to find values of [latex]x[/latex] to do the job. If you think about it, there are no [latex]x[/latex] values that can make it happen. Why?  Because in order for the rational expression to become zero, the NUMERATOR MUST BE ZERO. But the numerator is not zero, in fact, it is 5!

This tells me that I could never find an input (domain) to have an output of zero (range).

Therefore, the range isall y-values but does not include y = 0. The open circle in the graph below denotes that [latex]y = 0[/latex] is excluded from the range.

This is our final summary for the domain and range of the given rational function.

---

Example 4: Find the domain and range of the rational function

[latex]\Large{y = {{{x^3}} \over {x – 2}}}[/latex]

The domain of this function is exactly the same as in Example 7. The idea again is to exclude the values of [latex]x[/latex] that can make the denominator zero. Obviously, that value is [latex]x = 2[/latex] and so the domain is all x values except x = 2.

To find the range, I will heavily depend on the graph itself. It is possible to sketch it by hand using more advanced graphing techniques but I will leave it for another lesson. Anyway, the graph shows that it covers all possible [latex]y[/latex]-values: goes up and down without bounds, and no breaks in between. Therefore the range is all y values.

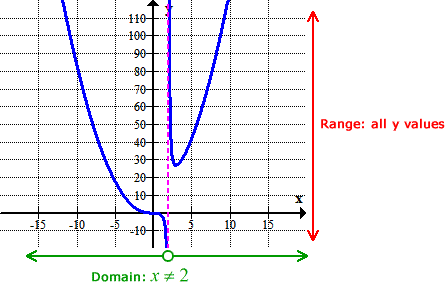
The domain and range written in two ways:

---

You may also be interested in these related math lessons or tutorials:

Domain and Range of Linear and Quadratic Functions