Factoring Trinomial Hard Case
Previously, we went over how to factor out a quadratic trinomial with a leading coefficient equal to 1. We called that type of trinomial as the “Easy Case“. This time around, we will deal with a trinomial having a nonzero leading coefficient not equal to [latex]+1[/latex] or [latex] -1[/latex] which we will call as the “Hard Case”.
Hard Case of a Trinomial

The following are the suggested steps used to factor this type of “hard” trinomial.
- Step 1: The basic strategy to factor this “hard” trinomial is to multiply the leading coefficient [latex]a[/latex] and the last coefficient [latex]c[/latex] to get a certain value called [latex]k[/latex]. Then, we find a factor pair (two numbers) of [latex]k[/latex] such that their sum (when added) gives us the middle constant [latex]b[/latex].

- Step 2: The appropriate factor pair of [latex]k[/latex] will be used to break the middle term into two terms. Suppose, the factor pair of [latex]k=mn[/latex].

- Step 3: Now, group them into two parentheses but keep the middle sign outside the parenthesis. The middle sign may be positive or negative depending on the situation.

- Step 4: Factor out each parenthesis completely. After doing so, the “leftover” expressions inside each parenthesis after factorization must be equal. Otherwise, go back and retrace your steps because more likely you committed an error.
- Step 5: And finally, since the “leftover” expressions inside the two parentheses are equal, we factor it out again to arrive at the final answer!
This will be much easier once we apply these steps using concrete examples. Here we go!
Examples of How to Factor a Trinomial (Hard Case)
Example 1: Factor the trinomial [latex]5x^2+16x+3[/latex] as a product of two binomials.
- First, multiply the leading and last constants of the trinomial. The product is 15.
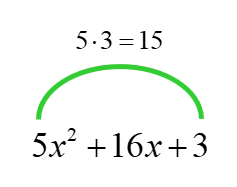
- Second, find the factor pair (two numbers) of 15 such that their sum would equal the middle constant, 16. After performing some trial and error, the only correct combination of two numbers is 1 and 15. Since
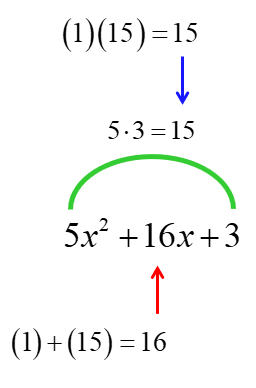
- Third, use the correct factor pair found above to replace the middle term [latex]16x[/latex]. Therefore, we have [latex]1x[/latex] and [latex]15x[/latex].
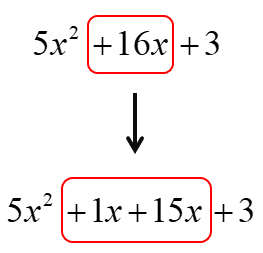
- Fourth, group them into two parentheses; however, keeping the middle sign outside.
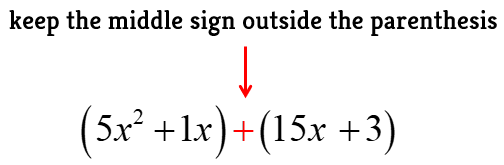
- Finally, factor out each parenthesis. The first parenthesis has the greatest common factor of [latex]x[/latex], while the second is 3. If you have done it right, the “leftover” expressions in the two parentheses must be the same. If that’s the case, perform one last factorization to get to the final answer!

So, the final answer here is
[latex]5{x^2} + 16x + 3 = \left( {5x + 1} \right)\left( {x + 3} \right)[/latex]
You may verify if the product of the two binomials is indeed the original trinomial using the FOIL Method.
Example 2: Factor the trinomial [latex]8x^2+2x-3[/latex] as a product of two binomials.
Multiply the first and last constants of the trinomial. That should be (8)(–3) = –24.

Find two numbers such the product is –24 and their sum is 2. By trial and error, the pair that should work is –4 and 6.
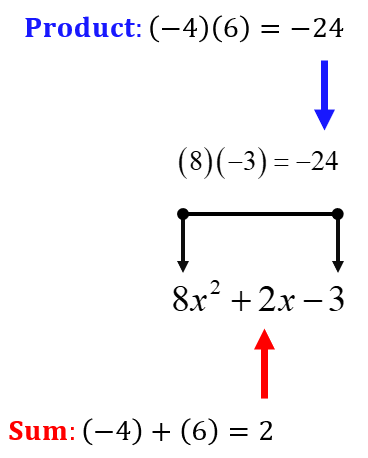
Use the two numbers (attached with variable [latex]x[/latex]) to replace the middle term of the original trinomial.
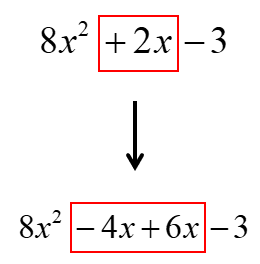
Separate them into two groups using the parenthesis symbol. Make sure to leave the middle sign outside.
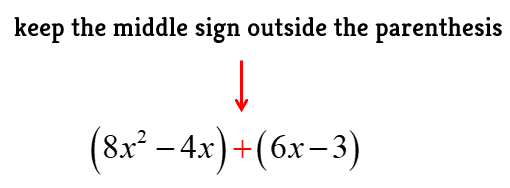
Now, it’s time to factor each expression in the parenthesis. The GCF of the first parenthesis is 4x while the second is 3. Eventually, we should obtain equivalent expressions in the two parentheses. Factor out that common expression [latex]2x-1[/latex] to get the final answer!

The final answer then is
[latex]8{x^2} + 2x – 3 = \left( {2x – 1} \right)\left( {4x + 3} \right)[/latex]
Check your answer by multiplying the two binomials using FOIL Method and see if it yields the original problem.
Example 3: Factor the trinomial [latex]12x^2-4x-1[/latex] as a product of two binomials.
The product of the leading and last constants is –12.
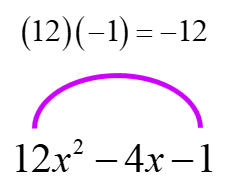
The factor pair with a product of –12 (multiply first and last constants, [latex]ac[/latex]) and a sum of –4 (middle constant, [latex]b[/latex]) is –6 and 2.
Since (–6)(2) = –12 and (–6) + (2) = –4.
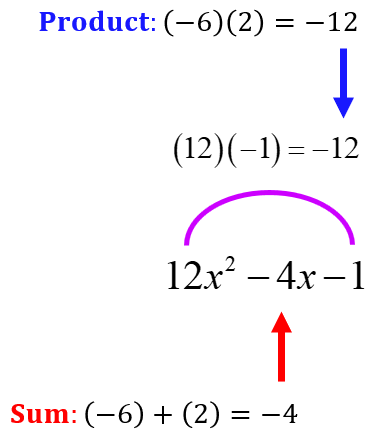
Rewrite the trinomial by replacing the middle term using the factor pair [latex]–6[/latex] and [latex]2[/latex]. Don’t forget to attach the variable [latex]x[/latex] to each of them.

Group them into two parentheses. Factor out the first and second parenthesis with their GCFs, [latex]6x[/latex] and [latex]1[/latex], respectively.
And then, perform final factorization with the common term [latex]2x-1[/latex] to arrive at the final answer.
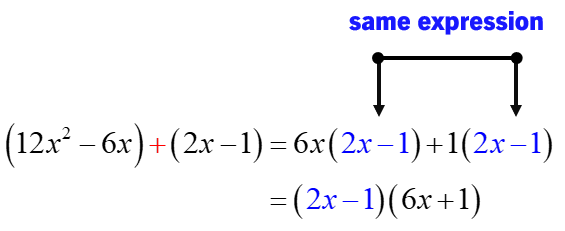
Therefore, the final answer is
[latex]12{x^2} – 4x – 1 = \left( {2x – 1} \right)\left( {6x + 1} \right)[/latex]
Example 4: Factor the trinomial [latex]4x^2-12x+5[/latex] as a product of two binomials.
Multiplying the first and the last constants give us (4)(5) = 20. Its factor pair whose sum equals the middle constant –12 is –2 and –10.
Just to check if our two numbers are right.
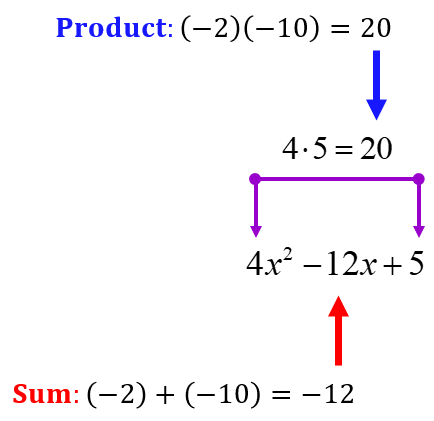
Using the correct factor pair, replace the middle term of the original trinomial by –2x and –10x.
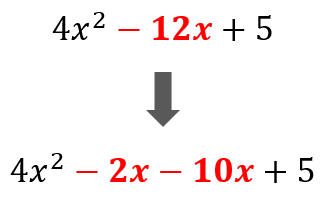
Group them into two parentheses while leaving the middle sign outside.
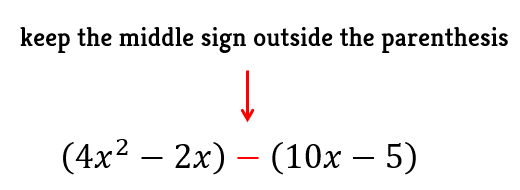
Factor out each parenthesis. The GCF of the first parenthesis is 2x while the second parenthesis is just 5. After performing this step, the expression inside each parenthesis must be equal, which it is! Factor out the common expression [latex]2x-1[/latex], and we are done!
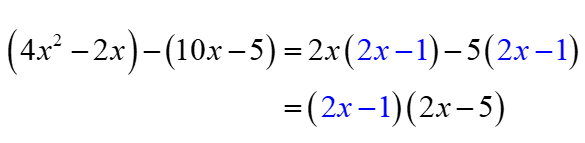
Thus, we have
[latex]4{x^2} – 12x + 5 = \left( {2x – 1} \right)\left( {2x – 5} \right)[/latex]
Example 5: Factor the trinomial [latex]4x^2-21x+5[/latex] as a product of two binomials.
If we multiply the first and last constant, we get (4)(5) = 20. Now think of two numbers when multiplied gives the product of 20, but when added together gives the middle constant, –21.
The correct pair of numbers is –1 and –20. Since
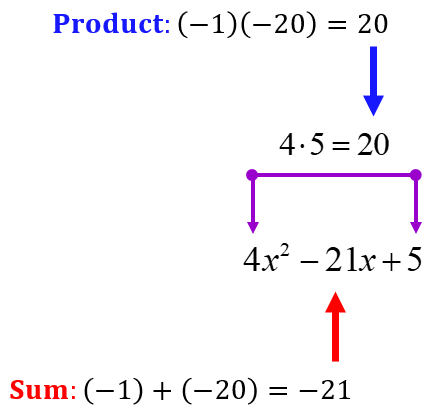
Replace the middle term of the original trinomial with the pair of numbers found. Make sure to attach variable [latex]x[/latex] to it.
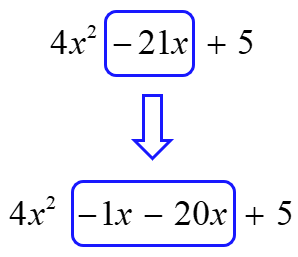
Group them using two parentheses. Keep the middle sign outside.
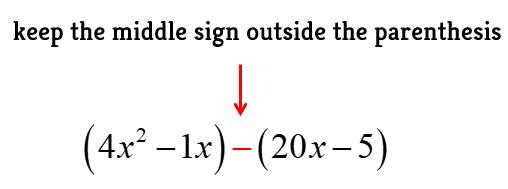
Then factor the expression in each parenthesis. The GCF of the first is [latex]x[/latex], while the second is 5. If the terms inside the parenthesis come out to be the same, that means we’re on the right track. Factor out that common expression to get the final answer.
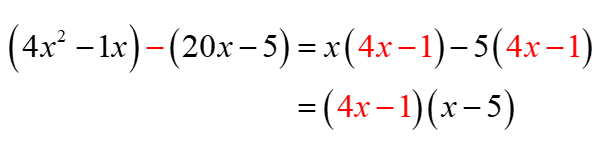
Thus, we have
[latex]4{x^2} – 21x + 5 = \left( {4x – 1} \right)\left( {x – 5} \right)[/latex]
Example 6: Factor the trinomial [latex]15x^2-8x+1[/latex] as a product of two binomials.
Solution:
The product of the first constant and the last constant is (15)(1) = 15. The factor pair of this product whose sum is the middle constant, –8, is –3 and –5.
Since (–3)(–5) = 15 and (–3) + (–5) = –8.
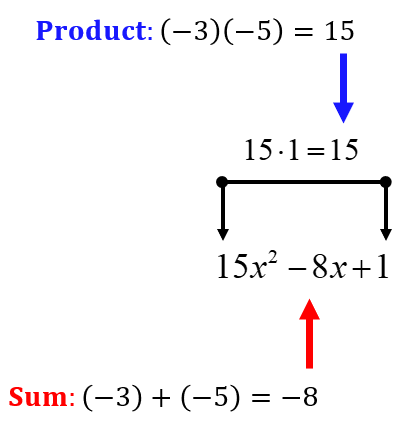
Use these two numbers to replace the middle term of the original trinomial. Make sure to attach a variable [latex]x[/latex] to each of them.
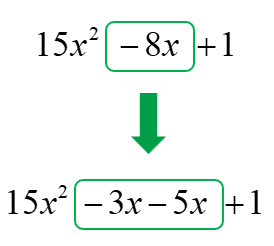
Separate them using parenthesis but keep the middle sign outside.
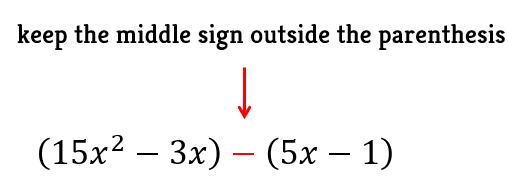
Factor out each parenthesis. The GCF of the first is [latex]3x[/latex], while the second is just 1. Finally, factor out the common binomial that arises from the previous step to get the final answer.

Therefore, we have
[latex]15{x^2} – 8x + 1 = \left( {5x – 1} \right)\left( {3x – 1} \right)[/latex]
Example 7: Factor the trinomial [latex]4x^2-8x-21[/latex] as a product of two binomials.
Solution:
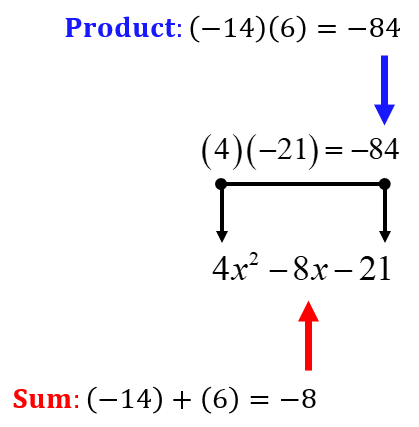
Find the product of the first and the last constants. That is (4)(–21) = –84. The product’s factor pair that when added yields the middle constant, –8 is –14 and 6.
It is the correct pair of numbers because (–14)(6) = –84 and (–14) + (6) = –8.
Replace the middle term of the trinomial by the two numbers found. Attach variable [latex]x[/latex] to each.
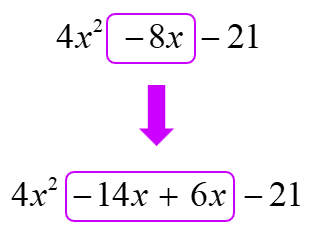
Group them using parenthesis. Keep the center sign outside.
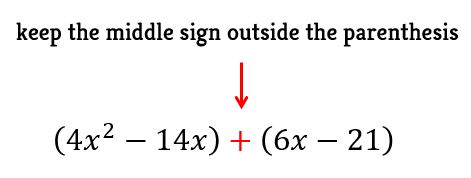
Factor each binomial in the parenthesis. The GCF of the first binomial is 2x while the second binomial is 3. If you’ve done this right, the “leftover” expressions in each parenthesis must be equal. If that’s the case, factor out that common expression to get the final answer

Therefore, we have
[latex]4x^2-8x-21=(2x-7)(2x+3)[/latex]
Example 8: Factor the trinomial [latex]9x^2+4x-5[/latex] as a product of two binomials.
Solution:
Multiplying the first and the last constants, I get (9)(–5) = –45. The factor pair of this product, –45, whose sum is the middle constant, 4, is just –5 and 9.
Use this to replace the middle term of the original trinomial. I would group them into two parentheses. Then, factor out each binomial and hope that two equal expressions will arise. Finally, factor out this common expression to get the final answer!!
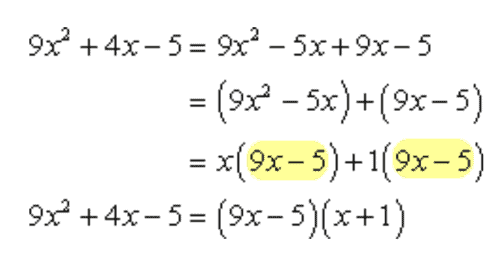
Example 9: Factor the trinomial [latex]4x^2-16x+7[/latex] as a product of two binomials.
Multiplying the first and the last constants, I get (4)(7) = 28. The factor pair of this product, 28, whose sum is the middle constant, –16, is just –14 and –2.
Use this to replace the middle term of the original trinomial. I would group them into two parentheses. Then, factor out each binomial and hope that two equal expressions will arise. Finally, factor out this common expression to get the final answer!
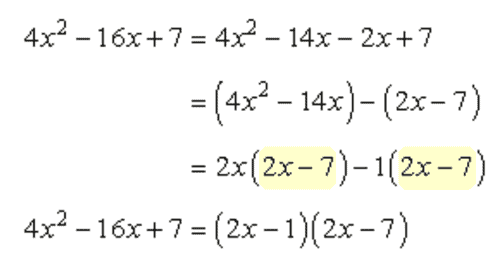
You may also be interested in these related math lessons or tutorials:
